关于子基的正则空间和相对正则性

刘德金

(德州学院数学科学学院,德州山东 253023)

关于子基的正则空间和相对正则性

刘德金

(德州学院数学科学学院,德州山东 253023)

给出了关于子基的正则空间和相对正则性概念,研究了各种正则性之间的关系,证明了各种正则空间的充要条件,丰富了一般拓扑学中的正则空间和相对正则性理论.

正则空间;正则性;子基;关于子基的正则空间;关于子基的相对正则性

1 引言

1996 年,文献[1]首次对相对拓扑空间及相对拓扑性质给出了系统的阐述,之后文献[2]对相对拓扑性质给了更加全面的描述,并得到许多新结果.另一方面,为了使粗糙集理论和覆盖广义粗糙集理论中的下近似集和上近似集都能分别地对应于某一拓扑空间子集的某种内部和闭包,文献[3]定义了拓扑空间的子集关于子基的内部和闭包,引入了拓扑空间的子集关于子基的开集和闭集,在此基础上文献[4]研究了拓扑空间关于子基的连通性概念.本文在文献[3-4]的基础上给出了拓扑空间关于子基的正则性概念,并将讨论相对拓扑性质的思想引入拓扑空间关于子基的分离性,给出了拓扑空间关于子基的相对正则性概念,并研究它们的性质.丰富了覆盖广义粗糙集理论研究的内容.

2 预备知识

文中关于子基的内部、闭包、开集、闭集、点的开领域等概念见文献[3],X的非空子空间Y在X中正则、Y在X中超正则、Y在X中强正则等概念可见文献[5-6],在此不赘述.

设X为非空集合,给定X上的拓扑T,如果β是T的子基,则该拓扑空间记为(X,T,β). X的子集A的补集记为～A.

引理1设(X,T,β)是拓扑空间,Y为X的子集,则T|Y是Y的拓扑,β|Y是Y的子基,并且对Y的任何子集A有

3 主要结果

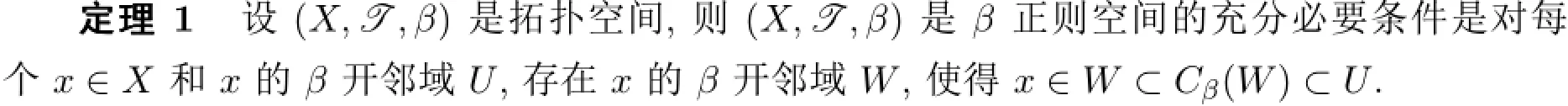
4 结束语

由上面的研究可知,当取子基为拓扑空间的基时,关于子基的正则空间就是一般拓扑学中的正则空间,关于子基的相对正则性就是一般拓扑空间中的相对正则性.因此关于子基的正则空间是一般拓扑学中正则空间的推广,关于子基的相对正则性是一般拓扑空间中相对正则性的推广.关于子基的正则性、关于子基的相对正则性也是拓扑空间的拓扑不变性.

[1]Arhangel′skll A V.Relative topological properties and relative topological space[J].Topology Appl.,1996, 20:1-13.

[2]Arhangel′skll A V.From classic topological invariants to relative topological properties[J].Scienticae Mathematicae Japonicae,2002,55(1):153-201.

[3]李进金.由子基生成的内部算子和闭包算子[J].数学进展,2006,35(4):478-484.

[4]李进金.关于子基的连通性[J].数学进展,2007,36(4):421-428.

[5]胡永利王尚志彭良雪.相对拓扑中的两个问题[J].纯粹数学与应用数学,2000,16(3):76-78.

[6]孙爱慧.拓扑空间的某些相对性质[J].吉林师范大学学报:自然科学版,2005(3):115-116.

The regular space and relative regularity with regard to a subbase

Liu Dejin

(School of Mathematical Sciences,Dezhou University,Dezhou253023,China)

This paper gives the concept of regular space and relative regularity with regard to a subbase,studies the relations between the various regularity,proves the necessary and sufcient condition for a variety of regular spaces,then enriches the generalization of regular space and relative regularity in the general topological space.

regular space,regularity,subbase,regular space with regard to a subbase, relative regularity related to a subbase

O189.1

A

1008-5513(2013)06-0559-06

10.3969/j.issn.1008-5513.2013.06.002

2013-06-14.

刘德金(1957-),教授,研究方向:几何与一般拓扑学.

2010 MSC:54A10,68T01