微网孤立运行时的调频策略研究

邵明燕，刘瑞叶，吕殿君

(哈尔滨工业大学电气工程及自动化学院，黑龙江 哈尔滨 150001)

0 引言

随着燃料的日益减少以及污染物排放增加，各国都加紧了研究可再生清洁能源的步伐，其中对包含风能、太阳能、储能以及负荷等的微网的研究尤为突出[1]。微网连接在主电网的中低压网络，可以运行于并网和离网两种模式下。当主电网正常运行时，微网内部的负荷主要由微网内微源提供，不足或多余的功率由主电网提供或吸收。当主电网出现故障或需要检修时，微网从电网上断开，形成一个孤立的微网[2-3]。为了使孤立微网仍然能够保证发电与用电平衡，就需要研究微网孤立运行情况下的频率调节控制。文献[4-6]研究了孤立微网的频率控制方法，但大都集中在对电力电子逆变器控制的层面上。文献[7]提出了一种包含多个电力电子接口的微源的微网的功率管理策略，可调度的微源响应系统频率的变化，达到调节微网频率的目的，各微源之间的调节相互独立。本文提出了一种系统层面的完整的孤立微网的调频策略，考虑各种微源对频率调节的不同特性和能力，通过设置参数决定各微源是否参与调频以及参与分量，使得孤立微网的频率能够经济快速的调节。

1 微网系统的结构

图1所示为连接到35 kV配电网上的一个简单微网系统的单线图，微网系统中包括多种发电单元，其中水电厂经馈线1接入，双馈式风力发电系统组成的风电场经馈线2接入，光伏电站经馈线3接入，储能系统经馈线4接入，集中负荷经馈线5接入。微网系统可随着断路器2的动作情况分别运行于并网和离网两种状态。主电网正常运行时，断路器2是闭合状态，双馈式风力发电系统运行于某一恒定桨距角下的最大功率状态点上，光伏发电系统以最大功率输出，储能系统不输出功率，水电厂运行于稳定的状态。主电网发生故障或检修时，断路器2断开，微网脱离电网而孤立运行。

图1 简单微网系统的单线图Fig. 1 Single architecture of microgrid

2 孤立微网的频率控制策略

2.1 各微源的调频控制

2.1.1 风力发电系统的调频控制策略

常规发电机的转子直接与电网相连，在系统频率发生变化时，转子的动能可以得到释放或吸收，如式(1)所示。

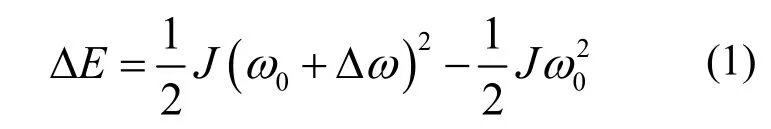
其中：ΔE为动能变化量；J为惯性时间常数；Δω为转速变化值；ω0为初始转速。在标幺值下ω=f，在式(1)两侧对时间t求导，并令ω=f，得

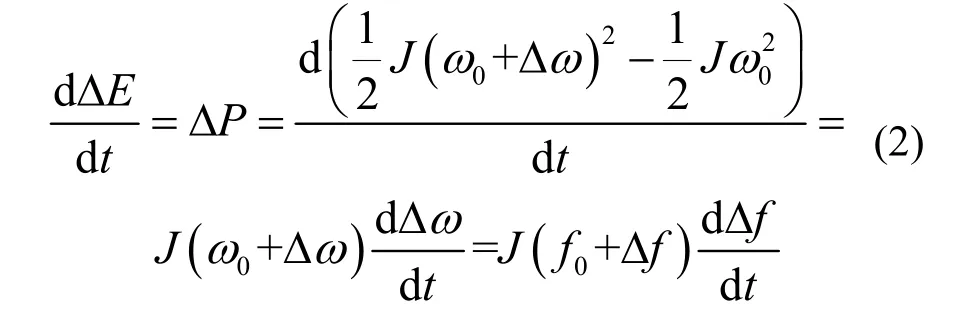
可见，系统频率变化将会引起转子转速变化进而改变输出功率。

双馈式风力发电系统转子侧是经双PWM变换器接入微网，转速不会自动响应系统频率的变化，为了达到控制频率的目的，需要在双馈式风力发电系统中增加辅助的频率控制，也就是一次调频控制。从式(2)可知，功率变化值与频率偏差以及频率偏差的微分有关，因此，风机响应微网系统频率变化的有功功率变化值可以设置为

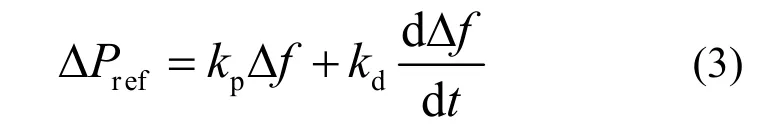
由式(3)产生的响应系统频率变化的辅助有功功率参考值变化量与最大功率曲线得到的参考值之和是DFIG新的功率参考值，如图2所示。

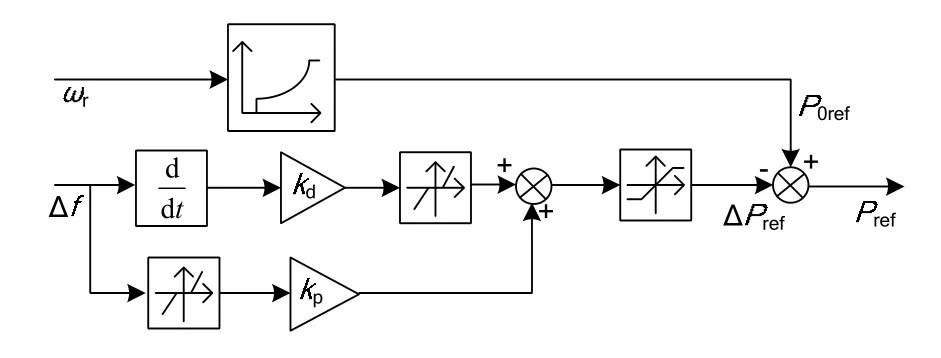
图2 风机一次调频控制器原理图Fig. 2 Control schematic diagram of primary frequency control

双馈式风力发电系统通常情况下是运行于最大功率跟踪控制下[8]，为了有效地进行频率控制，当负荷分量变化周期长、幅度大时，就需要风机的输出功率留有一定的冗余，参与二次调频。

风力机输出的最大功率在标幺值下可以表示为

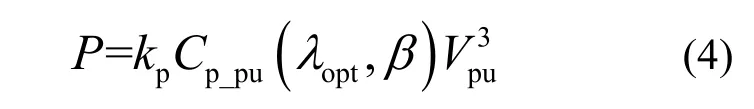
其中：Cp_pu为最大风能利用系数；Vpu为风速；β为桨距角为最优叶尖速比Vpu=1时的有功功率；Cp为桨距角 β和叶尖速比λ的函数，如式(5)所示。

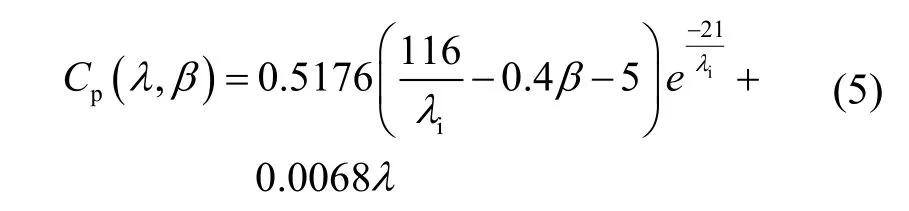
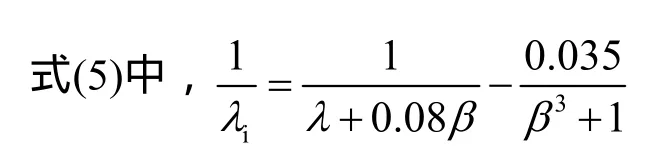
从式(4)可知，在一定风速下，风机输出功率的大小由风能利用系数决定。而风能利用系数Cp与桨距角β以及叶尖速比λ有很大的关系，可通过图3的曲线表示。由图3可以看出，桨距角变化时，最优叶尖速比以及最大风能利用系数均发生变化，随之风机输出功率发生改变。因此，可以通过设置桨距角初值使得风力发电系统具有一定的调节容量，并且通过调节桨距角改变风机输出功率。从式(4)和式(5)可以看出桨距角、最优叶尖速比以及风机输出功率之间的关系非常复杂，对于一定的调节功率，很难得出应有的桨距角调节量。本文通过曲线拟合的方式得出最优叶尖速比与桨距角的关系，使得式(5)中风能利用系数为单变量桨距角的函数，然后再拟合出桨距角与风能利用系数的多项式，分别如式(6)、式(7)所示，拟合度分别为99.7%，99.9%，最终得到输出功率与桨距角的关系。拟合出的桨距角与最优叶尖速比以及风能利用系数的曲线分别如图4、图5所示。

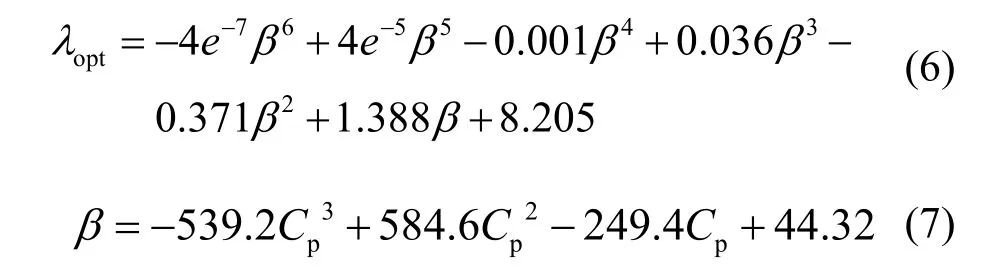
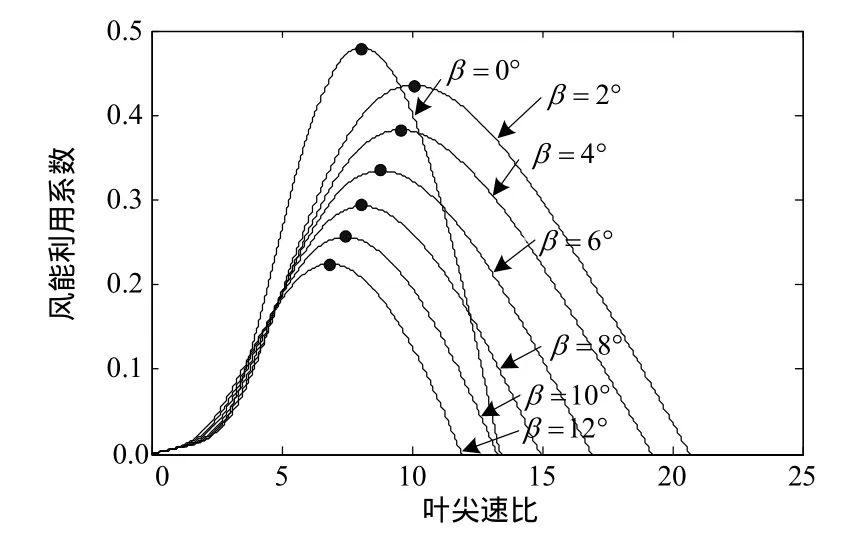
图3 风能利用系数与叶尖速比和桨距角的关系Fig. 3 The relationship among Cp, λ and β

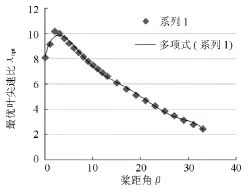
图4 桨距角与最优叶尖速比的关系曲线图Fig. 4 The relationship curve between λ and β

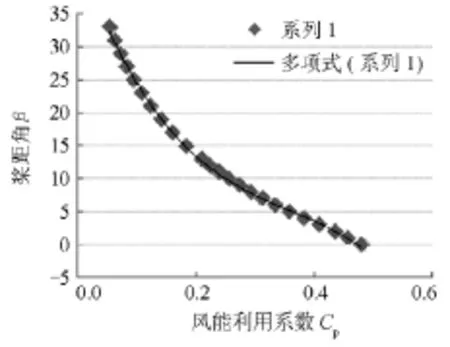
图5 桨距角与风能利用系数的关系曲线图Fig. 5 The relationship curve between Cp and β

将式(4)代入式(7)中得到桨距角与风机输出功率之间的关系，如式(8)所示。

根据式(4)~式(8)可以设计出风力发电系统的二次调频控制器，如图6所示。ΔP为功率的需要调节值，Ppu为风机初始输出功率，V为风速标幺值，Pnom为风力发电系统额定功率，Cpnom为风能利用系数额定值。当系统频率发生变化，可以由微网的功率管理系统分配给风电场一定的调节功率ΔP，与原输出功率相加得到风电场需要输出的功率，通过式(8)转换为风机的桨距角命令，实现通过调节桨距角改变风电场有功出力的控制。

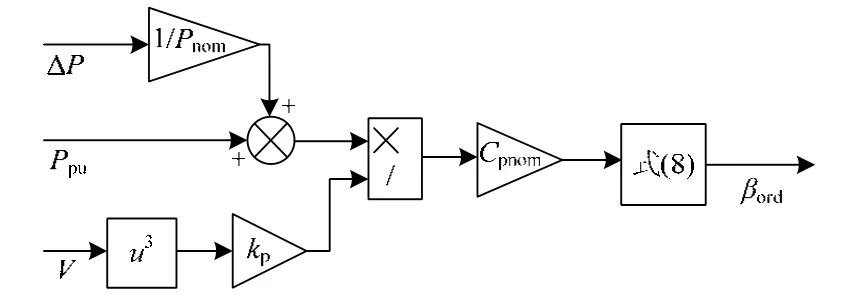
图6 风机二次调频控制器原理图Fig. 6 Control schematic diagram of second frequency control

2.1.2 蓄电池系统的调频控制

蓄电池是可调度的微源，采用PQ解耦控制的蓄电池系统的有功功率、无功功率由交流侧电流的id、iq分量单独控制[9]，其中为交流侧电压幅值。蓄电池的调频控制器如图7所示，P*为微网管理系统发出的调节功率值，Q*为无功功率参考值，在本文中设置为0。

2.2 微网的频率控制

微网的频率反应了微网系统发电与用电的平衡度，微网在孤立运行时的频率控制是通过调节各微源的有功出力完成。频率控制包括三个模块，一是调节功率产生模块，二是功率分配模块，三是各微源的调频控制器模块。调节功率产生模块与功率分配模块统称为微网功率管理模块。调节功率产生模块接收微网系统中的实时数据，转换为微网的调节功率，然后通过功率分配模块将调节功率按照参与分量分配给各微源的调频控制器，如图8所示。

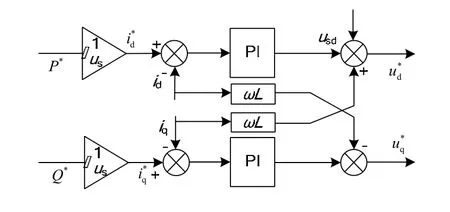
图7 蓄电池调频控制原理图Fig. 7 Control schematic diagram of battery frequency regulation

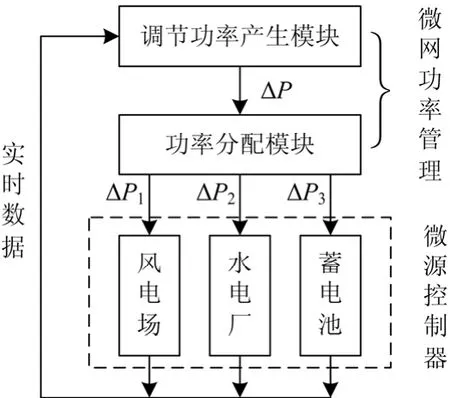
图8 频率控制的模块关系图Fig. 8 The relation graph among modules of frequency control

2.2.1 调节功率产生模块

调节功率产生模块根据系统的实时数据，计算当前所需调节的功率值，采用PI控制的调节功率如式(9)所示。

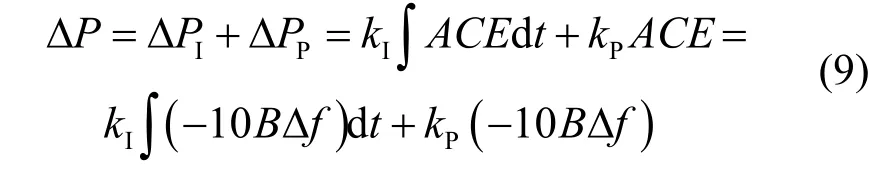
式中：DPP、DPI分别为比例分量和积分分量；kP、kI分别为比例增益和积分增益系数；ACE为区域控制偏差；B为频率响应系数，单位为MW/0.1Hz。

2.2.2 功率分配模块

微网系统中各种微源调频特性以及能力各不相同，水电属于常规电源，安装有调速器和调频器的水轮发电机具有相对较慢的静态频率特性。而从2.1节分析可知，双馈式风力发电系统的一次调频功能通过改变转子转速完成，调节速度很快，二次调频功能通过调节桨距角实现，调节速度相对较慢；蓄电池系统输出功率可调度，并且响应速度非常快，考虑到蓄电池的实际容量以及寿命，蓄电池有功功率出力最终需要归零[10]。在t=t1时刻，孤立微网系统频率低于额定值，各微源的频率响应特性示意曲线如图9所示。考虑到各个微源的调频特性以及经济性均不同，在进行微网频率控制时将有调频能力的微源分为传统微源和可再生微源两类，当系统需要调频时由可再生能源首先调频，达到调节极限时传统微源参加调频。每一类的调节分量按式(9)计算，并根据各微源的调频速度和调频容量分配调节功率。各微源的调节功率计算方法为

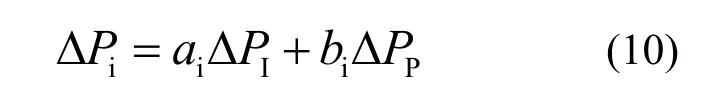
式中，ai、bi为分配系数，ai与调节容量有关，bi与调节速度有关。微网功率管理系统调节功率产生及分配原理可如图10所示。

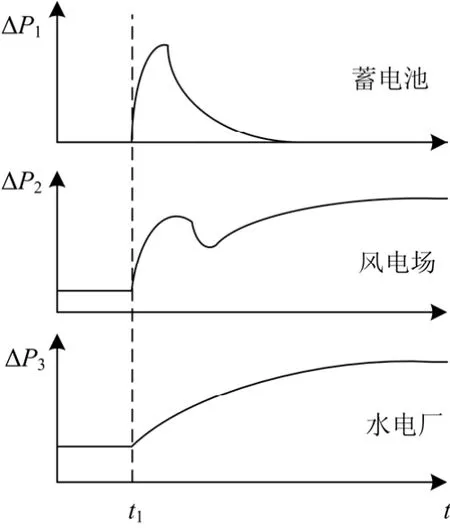
图9 各微源的频率调节特性Fig. 9 Frequency regulation characteristics of microsources

图10 调节功率产生及分配原理图Fig. 10 Production and distribution of regulated power

3 调频策略仿真验证

使用Matlab/Simulink仿真软件建立如图1所示的微网系统，微网运行于离网模式下。水电厂额定容量为100 MW，风电场额定容量为25 MW，光伏电站额定容量为1.6 MW，蓄电池容量为3 MWh。根据2.2.2分类原则，本论文建立的微网中第一类调频微源是蓄电池和风力发电，第二类是水电厂。风电场和蓄电池系统安装有2.1提出的调频控制器，水电厂安装调速器和调频器，设置在t=10 s增加3 MW负荷，在t=40 s再增加8MW负荷。风电场是通过调节桨距角实现有功功率出力的改变，因此图10中判定依据可以是风电场桨距角是否调节到0°或最大限制45°，从而决定水电厂是否参与二次调频。微网功率管理模块参数分别为B=5 MW/0.1 Hz，k1I=2，k1P=0.15，a11=0.8，a12=0.2，b11=0，b12=1，k2I=1，k2P=4.1，a21=1，b21=1。ΔP11、ΔP12、ΔP21分别是蓄电池、风电、水电的调节功率，仿真结果如图11~图14所示。

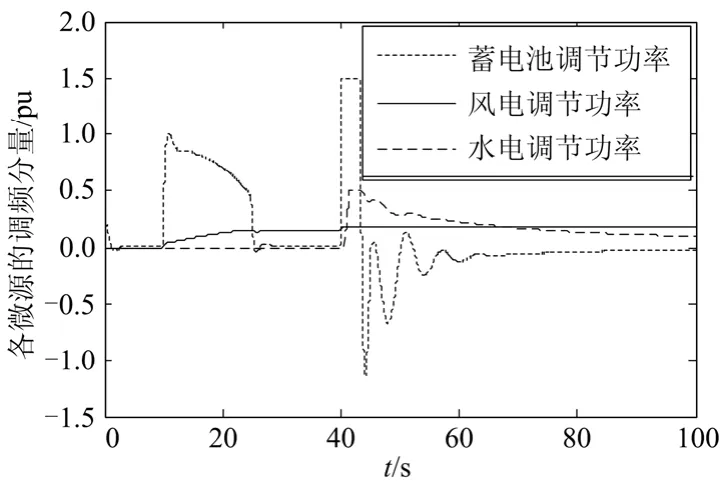
图11 各微源的调频分量计算值Fig. 11 The calculated value of regulated power of microsources

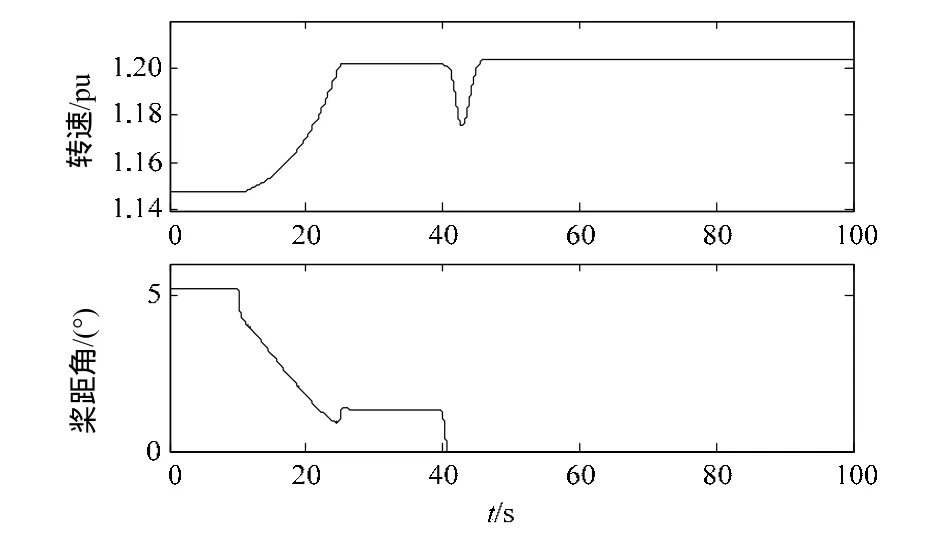
图12 风机的转速和桨距角Fig. 12 Speed and angle of DFIG

图11 所示为系统发生负荷突增时由功率分配模块产生的各微源调节功率值。图12所示为调频控制下风电场转子速度和桨距角的曲线，从曲线可以看出，在负荷增加3 MW时，因为频率波动不大，转速基本没有变化，直到桨距角调节响应后转速上升并稳定于1.2 pu，增加了风电场的有功出力；在负荷又增加8 MW后，频率扰动较大，风电场产生的一次调频辅助量较大，转速迅速下降而释放转子动能，风电场接收到功率管理模块产生的调节功率，桨距角由 1.2°开始减少并很快达到调节极限值 0°，转子转速从最低点1.17上升并最终稳定运行于1.21 pu。

图13所示为频率扰动下各微源的有功功率出力，在调频控制器的作用下各微源有功出力发生相应的变化，在t=10 s负荷有功功率增加3 MW，因风电未达到调频极限，水电厂不参与二次调频，只有风电场和蓄电池参与调频，并且最终蓄电池有功出力调节到0；当t=40 s时负荷再增加8 MW，风机桨距角调节到 0°，风电场达到调频极限，水电厂参与二次调频，从图13中可以看出风电场在一次调频控制下有功出力先增加后减少，二次调频动作后，有功出力迅速增加并很快达到调节极限，最终以最大功率输出，水电厂在二次调频作用下有功出力增加，蓄电池输出功率响应系统频率的变化并最终调节到0。图14给出了微网在负荷变化的情况下有无风电参与调频的两种模式下的频率响应。两种模式下的频率变化对比曲线可以看出在风电场参与调频的模式下微网的动态频率偏差在电网正常运行的频率偏差限值±0.5 Hz内，而在模式2的情况下，冲击负荷为8 MW时频率偏差高达2 Hz，已经严重影响系统的正常运行，并且模式2调频速度明显慢于模式1的情形。可见风电参与调频提高了微网的抗频率干扰能力，并加快了响应速度。

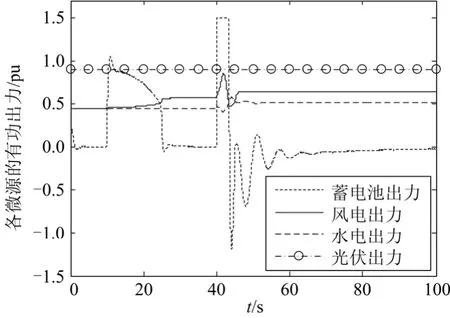
图13 微网中各微源有功出力Fig. 13 Output power of microsources

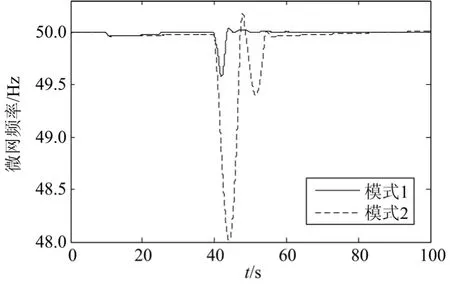
图14 微网的频率曲线Fig. 14 Frequency curve of microgrid

仿真结果表明了孤立运行的微网在系统负荷发生突变时频率控制系统能够合理、经济地分配调节功率，微网的当地控制器能够准确地响应调节功率而改变自身的有功出力，仿真结果验证了所提出的孤立微网调频策略的正确性和风电参与调频的必要性。

4 结论

本文从微源的实际模型出发，详细设计了风电场和蓄电池的调频控制器，提出了一种经济有效的微网孤立运行时的调频控制策略，并通过对比微网孤立运行时有无风电场参与调频两种情形下频率的变化，验证风电参与调频的必要性和有效性。提出的频率控制策略对后续微网的经济运行以及调度打下基础。

[1] 郭天勇, 赵庚申, 赵耀, 等. 基于风光互补的微网系统建模与仿真[J]. 电力系统保护与控制, 2010, 38(21):104-106.GUO Tian-yong, ZHAO Geng-shen, ZHAO Yao, et al.Modeling and simulation of microgrid system based on wind-solar hybrid[J]．Power System Protection and Control, 2010, 38(21): 104-106.

[2] 肖宏飞, 刘士荣, 郑凌蔚, 等. 微型电网技术研究初探[J]. 电力系统保护与控制, 2009, 37(8): 114-118.XIAO Hong-fei, LIU Shi-rong, ZHENG Ling-wei, et al.A preliminary research on microgrid technology[J].Power System Protection and Control, 2009, 37(8):114-118.

[3] 张纯, 陈民铀, 王振存. 微网运行模式平滑切换的控制策略研究[J]. 电力系统保护与控制, 2011, 39(20):1-5.ZHANG Chun, CHEN Min-you, WANG Zhen-cun.Study on control scheme for smooth transition of micro-grid operation modes[J]．Power System Protection and Control, 2011, 39(20): 1-5.

[4] WANG Yang, LU Zong-xiang, MIN Yong, et al.Comparison of the voltage and frequency control schemes for voltage source converter in autonomous microgrid[C] // PEDG 2010 2nd IEEE International Symposium, 2010: 220-223.

[5] Delghavi M B, Yazdabi A. A control srategy for islanded operation of a distributed resource (DR) unit[C] //PES．Power and Energy Society General Meeting, 2009:1-8.

[6] MAO Biao, ZHANG Bu-han, WANG Jiang-hong, et al.Dynamic modelling for distribution networks containing dispersed generations and energy storage devic[C] //International Conference on Power System Technology,2010: 1-6.

[7] Kim Jong-Yul, Jeon Jin-Hong, Kim Seul-Ki, et al.Cooperative control strategy of energy storage system and microsources for stabilizing the microgrid during islanded operation[J]. IEEE Trans on Power Delivery,2010, 25(12): 3037-3039.

[8] Ma H T, Chowdhury B H. Working towards frequency regulation with wind plants: combined control approaches[J]. IET Renewable Power Generation, 2010:308-310.

[9] 杨文杰. 光伏发电并网与微网运行控制仿真研究[D].成都: 西南交通大学, 2010.YANG Wen-jie. Simulation and research of grid connected photovoltaic generation and micogrid operation control[D]. Chengdu: Southwest Jiaotong University, 2010.

[10] Kim Jong-Yul, Jeon Jin-Hong, Kim Seul-Ki, et al.Cooperative control strategy of energy storage system and microsources for stabilizing the microgrid during islanded operation[J]. IEEE Trans on Power Delivery,2010, 25(12): 3037-3039.