基于目标全息反馈的统一潮流控制器非线性控制设计

李秋文，李啸骢，邓裕文，王 乐，游晓枫，柴小亮

（1.广西电网公司电力调度控制中心，广西 南宁 530023； 2.广西大学电气工程学院，广西 南宁 530004）

0 引言

统一潮流控制器（UPFC）是柔性交流输电系统（FACTS）的一个新控制装置，其不仅可以控制线路的潮流和节点电压，还能有效地改善电力系统的暂态稳定性，是FACTS家族中最具代表性的一员。近年来对UPFC控制研究比较多，包括智能控制算法、优化控制算法、线性最优控制算法以及基于微分几何原理的非线性控制算法[1-9]。而基于状态方程的线性、非线性控制设计方式发展比较成熟，易为学者广泛接受。而不管是何种控制理论，其目的都是设法将所需的控制目标信息反馈给控制规律以期得到更优的控制效果。此外，后期研究发现在非线性控制设计中某些目标状态量往往会产生静态偏移的问题，而输出函数的选取对控制系统的性能有重要影响，当输出函数选取为某些目标状态量的线性组合时往往能消除静态偏移[10-14]。同时，若能将全部控制目标信息反馈给控制规律，并在性能指标中对所有控制目标进行有效约束也能协调好控制系统的动、静态性能，解决静态偏移的问题。这就是后来学者所提出的一种新的控制设计方案，即目标全息反馈控制设计方法[15-20]。

在UPFC控制系统中，一般主要关心的控制目标有：接入点电压、有功功率、角速度、线路上传输功率等。如何使这些控制目标在性能指标中得到有效约束，以确保其动、静态性能，并使获得的控制规律包含全部控制目标的反馈信息则是控制设计所要解决的首要问题之一。本文采用目标全息反馈非线性控制设计方法，求解出包含全部控制目标反馈信息的非线性控制规律，完成了UPFC目标全息反馈控制系统的设计。在单机无穷大系统上的仿真结果表明：UPFC目标全息反馈控制设计方案，不仅能有效协调控制系统各控制目标的动、静态性能，还能有效解决部分系统中出现的控制目标静态偏移的问题，提高电力系统暂态稳定性。整个设计过程简单，思路清晰，易于掌握和实用。

1 UPFC的微分代数系统模型

设UPFC安装在发电机出口升压变压器的高压母线侧，经双回线与无穷大系统相连。UPFC的两个逆变器的输出分别通过并联变压器和串联变压器与系统线路相连，其接入系统的原理结构图如图 1所示。对于接入电力系统的UPFC的作用，在此可以用两个电压源来等效， UPFC等值电路图可表述如图2所示。

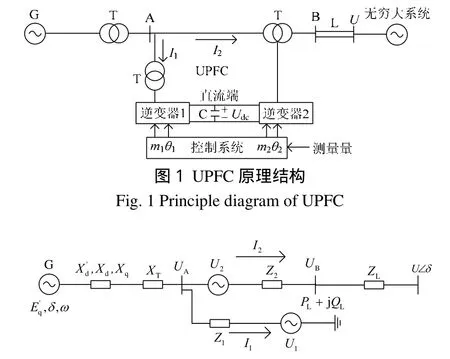
图2 UPFC等值电路Fig. 2 Equivalent circuit of UPFC

图中：21,UU 分别为两侧逆变器等效电压源；U为无穷大母线电压；AU 为UPFC接入点电压；C是直流电容；cU 是电容两端的电压；21,II 为UPFC并联侧和串联侧电流；2121,,,qqmm分别为两侧逆变器的脉宽调制比与相角调制量。UPFC通过调节 的状态来控制交流侧输出电压（21,UU ）的幅值与相角，其关系如下（假设两侧逆变器采用SPWM）：

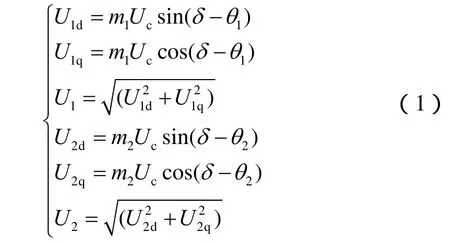
对此动态调节过程，可以用一阶惯性环节来等效[6]，即

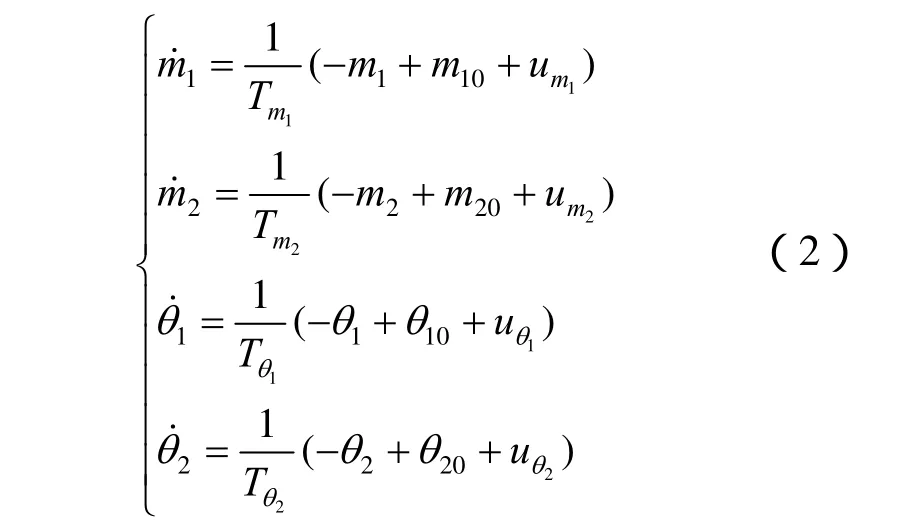
考虑电容的充放电过程是由逆变器两侧不平衡功率引起，故在此用一阶微分方程表示为

式中：1dU ，1qU ，2dU ，2qU 是经Park变换后的逆变器的两侧输出电压；1dI,1qI,2dI ,2qI 是经Park变换后线路两侧的电流。当系统处于稳态时，不平衡功率为零，即有

同时，基于d-q0坐标系下基本电路方程，可将线路潮流LP、LQ ，发电机有功输出AP表示为

式中：d和w分别代表发电机功角和发电机转子角速度；mP代表发电机的机械输入功率；jT为发电机组的转子惯性时间常数；D为发电机阻尼系数。

由图2可知，此时接入点电压可表示为（设空载电势qE¢为常数）

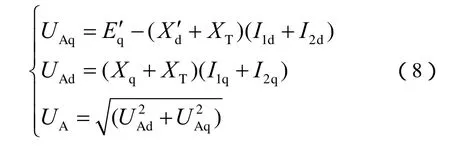
结合式（2）、式（3）、式（7）可得出UPFC控制系统模型为

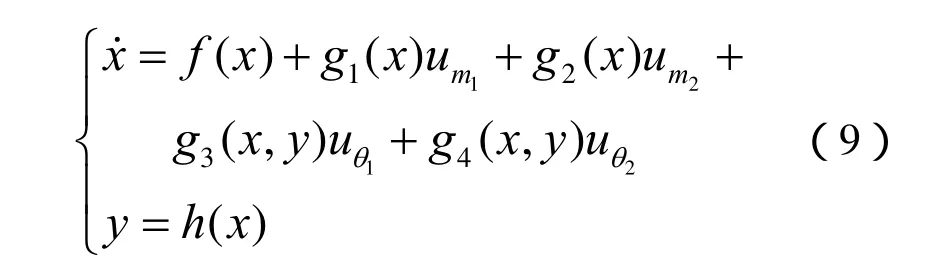
2 UPFC目标全息反馈控制设计

针对所建立的UPFC非线性控制系统式（9），运用目标全息反馈非线性控制设计方法进行控制规律设计[15-20]。

UPFC在运行过程中，一般主要关心的控制目标有：接入点电压、有功功率、角速度、线路上传输功率等。对此我们选取以下多目标状态方程：

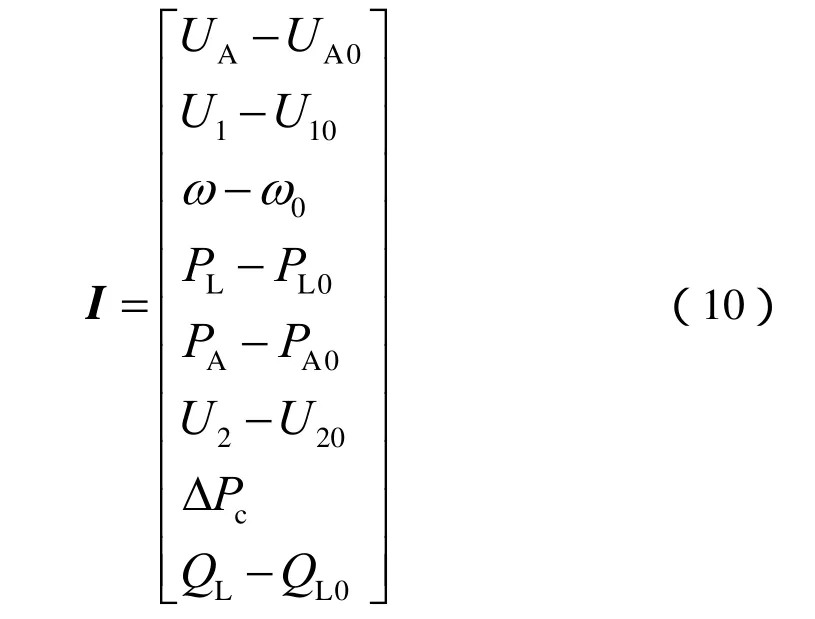
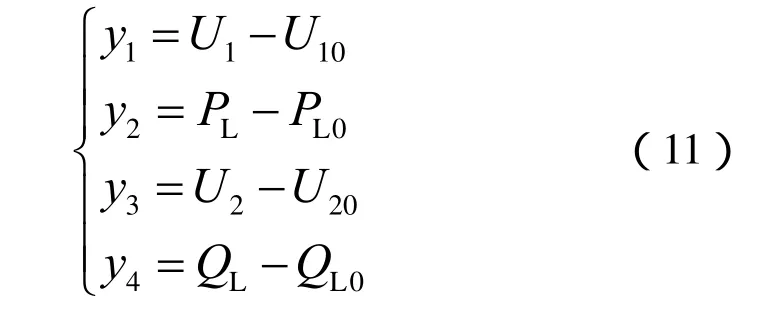
对于多输入多输出非线性系统（9），当输出函数选取为（11）时，由非线性控制设计方法不难得出[21]

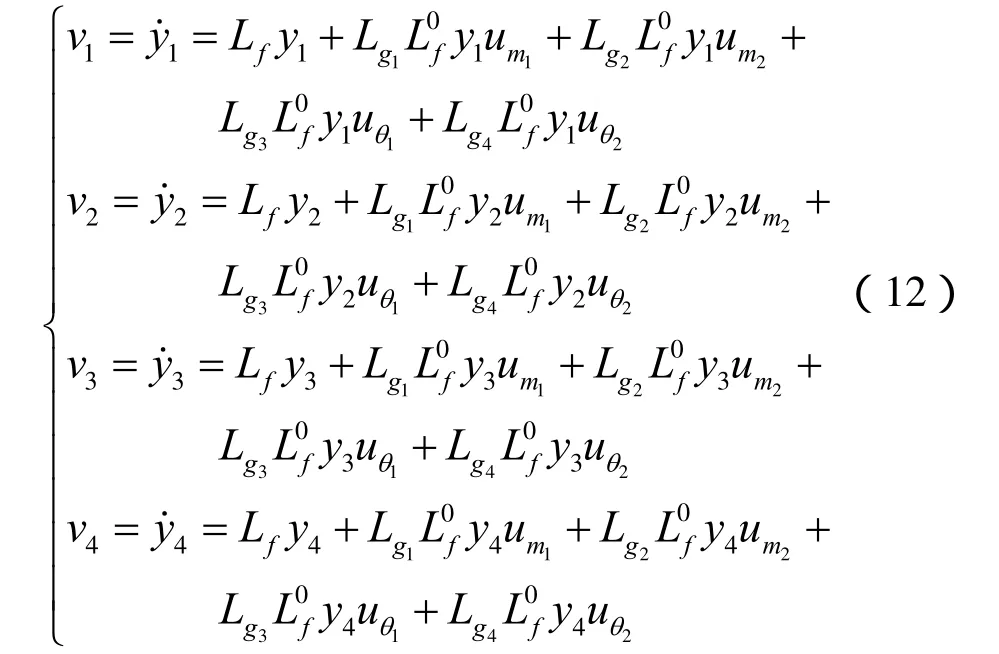
至此，即可反解出x非线性空间的控制规律为

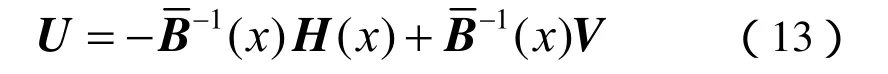
其中，

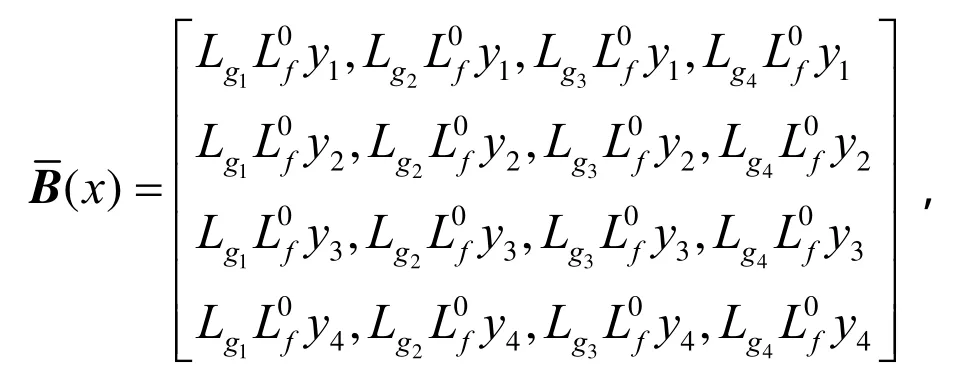
此外，由目标全息反馈控制设计理论知[15-20]：对于多目标状态方程组（10），在此构造一线性系统并假定其满足布鲁诺夫斯基标准型；同时假定存在一线性反馈控制规律V使得该系统有效稳定。

据此，可构造得到如式（14）所示多目标线性系统。

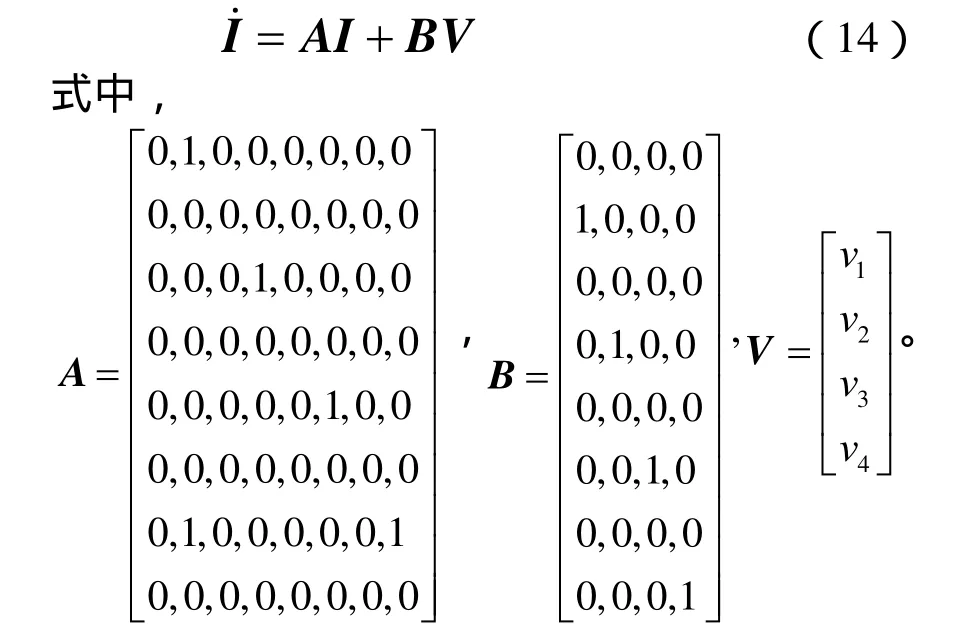
此时，此线性系统反馈控制规律V可由线性最优控制理论获得，即

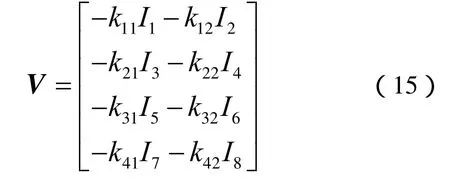
将式（15）代入式（13）即可求解出原系统的非线性控制规律U，至此完成UPFC目标全息反馈非线性控制设计。

评注2 用线性最优控制理论求解系统（14）时，可以得到如下性能指标：

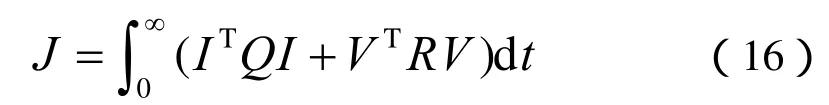
由此，不难看出目标控制量I均能在二次性能指标中得到有效约束，一旦这些量发生偏移，控制律便会迅速做出反应，以约束这些目标控制量的偏移，从而有效保障了控制系统的动、静态品质。

3 系统零动态稳定性分析

通过上述的设计过程可知，原非线性系统中除了4阶线性系统外，还存在着3阶零动态系统。而原系统的渐近稳定性是由零动态系统的稳定性来决定的。故下面对其零动态系统的稳定性进行必要的分析和讨论。

由非线性控制设计原理可知，该系统可选取如式（17）坐标变换。

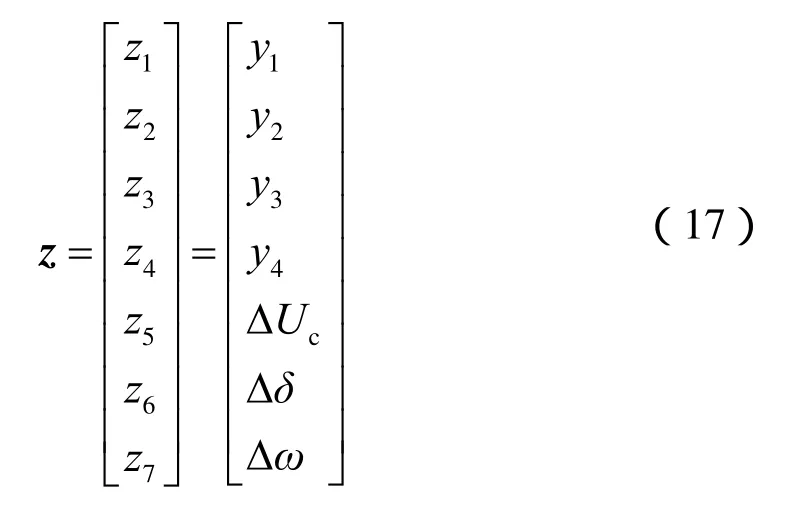
至此，可将原系统（9）变换为

分析式（9）、式（18）可得其零动态系统为

其中：Lz为线性系统；Nz为非线性系统，即零动态系统；且有

当线性子系统进入稳定后必有L0=z，此时由式（19）可得

下面考查零动态系统（20）的稳定性。

将式（20）在初始运行点进行泰勒展开得（初始点运行工况请参阅4.1系统参数）：

式中，

由式（21）可知，矩阵NA 的特征根分别为10.8319i。可见，其零动态系统是稳定的。因此，原系统亦是稳定的。

为验证所设计的目标全息反馈非线性控制器的调节性能，以下进行系统的仿真实验。

4 UPFC仿真实验

4.1 系统参数

为检验UPFC的目标全息反馈非线性控制方式的控制效果，本文以单机无穷大系统为例，并与线性最优控制方式进行了比较。

在UPFC线性最优控制方式设计中，首先对系统式（9）在初始点进行线性化，得到

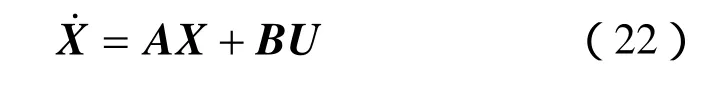
式中：A、B为系数矩阵；U是反馈控制规律；

同时，由线性最优控制设计原理知其反馈控制规律为

其中，K为反馈系数矩阵，在此取为

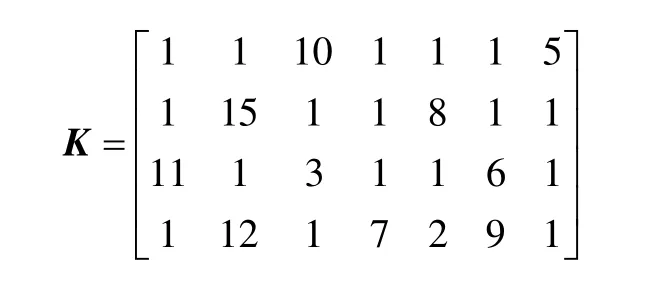
此外，在UPFC目标全息反馈控制设计中，所选取的系数矩阵为：

仿真曲线说明：蓝实线代表目标全息反馈控制方式（NCOHF）；绿虚线代表线性最优控制方式（LOP）。

4.2 调功扰动仿真

系统在0.5 s时，原动机有功功率调高10%，系统有关状态量响应曲线如图3所示。图3(a)表明在目标全息反馈控制方式（NCOHF）的作用下，调功扰动时接入点电压均没有发生静态偏移，而是稳定在电压给定值上，同时不难看出NCOHF表现得更优，抗扰能力强，动态过程中几乎没有发生任何振荡，这是由于 NCOHF包含了控制目标，使其在二次性能指标中得到有效约束，避免了静态偏移。图3(b)表明，NCOHF控制方式对发电机有功功率具有很好的跟踪特性。图3(c)中，由于接入点电压的变化使得线路上的有功损耗各不相同，最终导致负荷端得到的有功功率略有不同。综观图3可见，由于NCOHF控制规律中包含了全部目标状态量，并在性能指标中得到有效约束，使得UPFC具有更优镇定功效，各目标量动、静态性能优越，且不产生静态偏移。

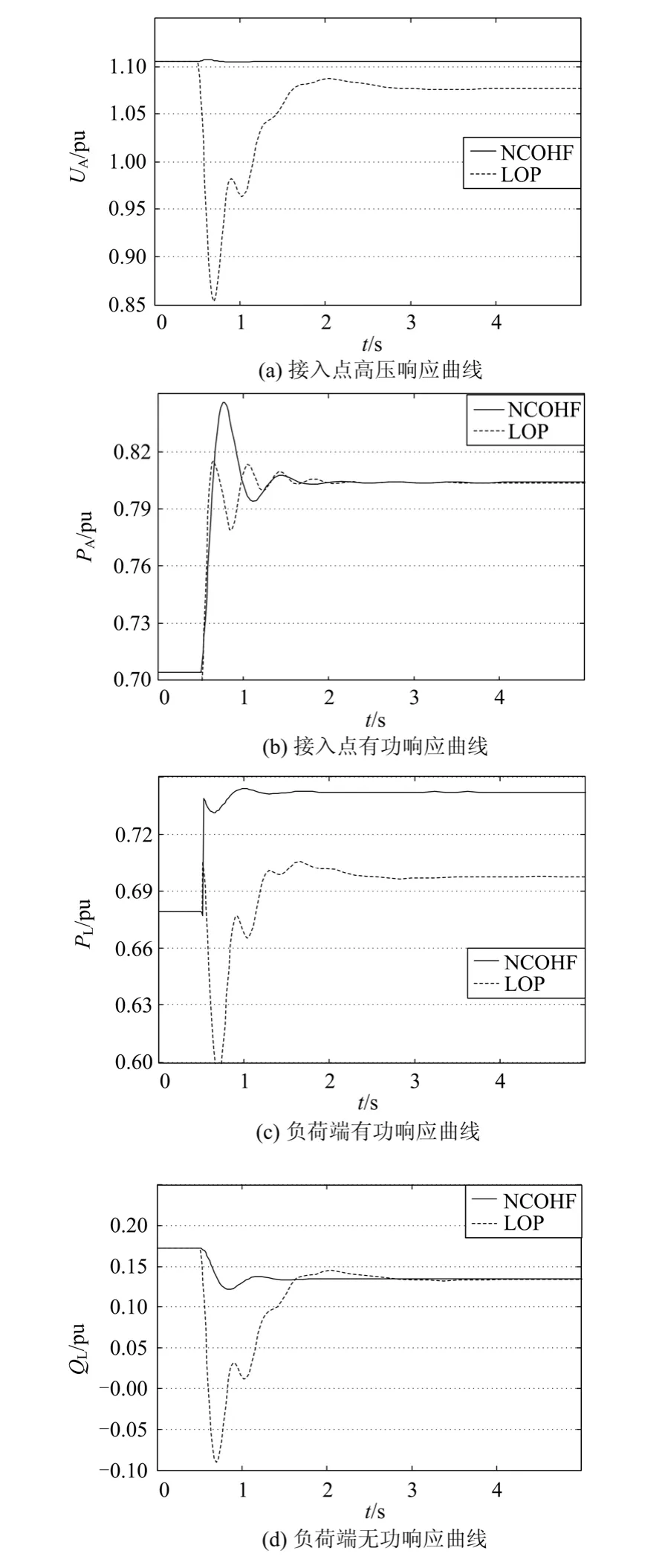
图3 原动机输入扰动时系统响应曲线Fig. 3 Responses of the system to disturbance of prime mover input

4.3 三相短路暂态仿真

系统在0.5 s时，负荷端发生三相短路，0.62 s时系统恢复正常，系统有关状态量响应曲线如图 4所示。

图4表明：在三相短路扰动中，NCOHF控制方式能有效地平息系统在暂态过程中的机械振荡，各控制目标动、静态品质较为优良。这是由于NCOHF控制规律中都包含了控制目标状态量，能够很好地对目标量进行惩罚。同时NCOHF的全部目标量均在反馈控制律得到体现，有效改善了系统的反馈信息，提高控制器综合性能，这也就是目标全息反馈控制方法更为优越的原因。

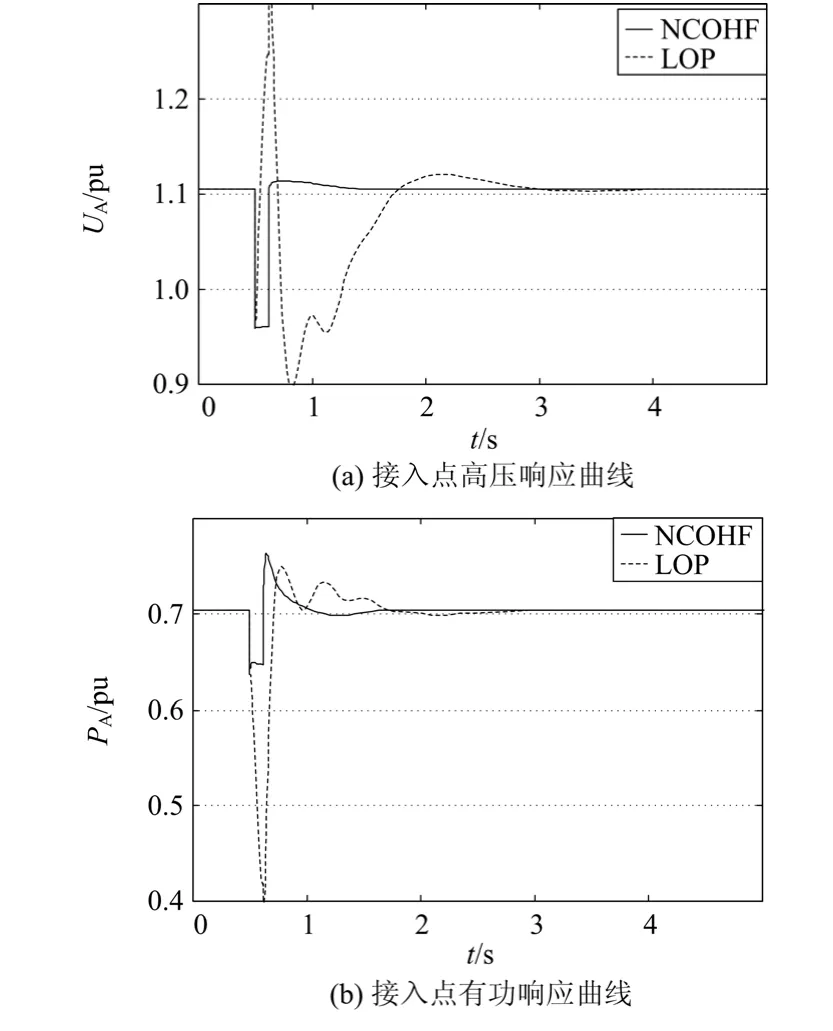
图4 三相短路时系统响应曲线Fig. 4 Responses of the system to disturbance of three-phase short circuit

5 总结

（1）本文针对统一潮流控制器（UPFC）非线性控制系统，运用目标全息反馈控制设计方法，将原系统非线性状态方程转换到以控制目标为状态量的线性空间，并结合线性最优控制理论，将线性系统中的全部目标控制量反馈到原系统控制规律中，完成目标全息反馈非线性控制设计。设计过程中，所需选取的参数较少且易获得，避免了非线性控制设计中 kc,参数选取所带来的难题，简化了控制设计过程。

（2）通过计算机仿真，验证了本文所设计的UPFC控制器能够很好地改善系统的动、静态品质，解决有功扰动中接入点电压静态偏移的问题；并有效快速地控制节点电压和线路潮流。表明NCOHF控制设计方案在协调控制系统动、静态性能方面的有效性与优越性。整个设计过程简单，思路清晰，便于掌握和实用。

[1] 张振华, 江道灼. 基于 MMC 拓扑的 UPFC 控制策略仿真研究[J]. 电力系统保护与控制, 2012, 40(3):73-77.ZHANG Zhen-hua, JIANG Dao-zhuo. Control strategy simulation of UPFC based on modular multilevel converters[J]. Power System Protection and Control,2012, 40(3): 73-77.

[2] 黄方能, 黄成军, 陈陈, 等. UPFC 稳定控制器的研究及应用[J]. 电力自动化设备, 2009, 29(3): 101-105.HUANG Fang-neng, HUANG Cheng-jun, CHEN Chen,et al. Study and application of UPFC stabilizer[J].Electric Power Automation Equipment, 2009, 29(3):101-105.

[3] 李兰英, 沈艳红. UPFC 控制器 IP 设计[J]. 电力系统保护与控制, 2010, 38(11): 104-108.LI Lan-ying, SHEN Yan-hong. IP design of unified power flow controller[J]. Power System Protection and Control, 2010, 38(11): 104-108.

[4] 侯丽, 鲁宝春. 一种新型的 UPFC 控制策略设计[J].电力系统保护与控制, 2008, 36(1): 33-36.HOU Li, LU Bao-chun. A new control strategy design of unified power flow controller[J]. Power System Protection and Control, 2008, 36(1): 33-36.

[5] 顾威，李兴源，魏巍. 一基于 UPFC 的风电场稳定性动态仿真研究[J]. 电力系统保护与控制, 2010, 38(11):70-74.GU Wei, LI Xing-yuan, WEI Wei. Simulation study on wind farm stability with UPFC[J]. Power System Protection and Control, 2010, 38(11): 70-74.

[6] 颜伟, 朱继忠, 徐国禹. UPFC线性最优控制方式的研究及其对暂态稳定性的改善[J]. 中国电机工程学报,2000, 20(1): 45-49.YAN Wei, ZHU Ji-zhong, XU Guo-yu. Enhancement of power system stability using linear optimal control strategy of UPFC[J]. Proceedings of the CSEE, 2000,20(1): 45-49.

[7] 袁志昌, 宋强, 刘文华, 等. 统一潮流控制器的非线性控制[J]. 电力系统自动化, 2005, 29(19): 36-39.YUAN Zhi-chang, SONG Qiang, LIU Wen-hua, et al. A nonlinear controller for unified power flow controller[J].Automation of Electric Power Systems, 2005, 29(19):36-39.

[8] 谢桦, 梅生伟, 徐政, 等．统一潮流控制器的非线性控制和对电力系统稳定性的改善[J]. 电力系统自动化,2001, 25(19): 1-5.XIE Hua, MEI Sheng-wei, XU Zheng, et al. Nonlinear control for UPFC to improve transient stability of power systems[J]. Automation of Electric Power Systems, 2001,25(19): 1-5.

[9] 奚玲玲, 艾芊, 陈陈. UPFC新型非线性控制策略[J].电力系统自动化设备, 2007, 27(4): 55-59.XI Ling-ling, AI Qian, CHEN Chen. Novel nonlinear control scheme of UPFC[J]. Electric Power Automation Equipment, 2007, 27(4): 55-59.

[10] 李啸骢. 发电机励磁控制系统调节器的抗扰设计[J].电力系统自动化, 1993, 17(9): 14-29.LI Xiao-cong. The anti-disturbance design of the synchronous generator excitation regulator[J].Automation of Electric Power Systems, 1993, 17(9):14-29.

[11] 李啸骢, 颜卓胜, 韦化, 等. U 型非线性抗扰励磁控制律设计[J]. 中国电机工程学报, 1999, 19(9): 71-75.LI Xiao-cong, YAN Zhuo-sheng, WEI Hua, et al.Anti-disturbance design of the nonlinear excitation regulator[J]. Proceedings of the CSEE, 1999, 19(9):71-75.

[12] 李啸骢, 程时杰, 韦化, 等. 具有多性能指标的汽轮发电机非线性综合控制[J]. 中国电机工程学报, 2003,23(4): 96-101.LI Xiao-cong, CHENG Shi-jie, WEI Hua, et al.Multi-index nonlinear integrated control for turbine generator unit[J]. Proceedings of the CSEE, 2003, 23(4)：96-101.

[13] 李啸骢, 程时杰, 韦化, 等. 输出函数在单输入单输出非线性控制系统设计中的重要作用[J]. 中国电机工程学报, 2004, 24(10): 50-56.LI Xiao-cong, CHENG Shi-jie, WEI Hua, et al.Important effection of the output function in SISO nonlinear control system design[J]. Proceedings of the CSEE, 2004, 24(10): 50-56.

[14] 李啸骢, 程时杰, 韦化, 等. 中间再热式汽轮发电机组的多指标非线性综合控制器的研究[J]. 电网技术,2004, 28(7): 1-6, 18.LI Xiao-cong, CHENG Shi-jie, WEI Hua, et al. Study on multi-index nonlinear integrated controller for rehear-type turbo generator unit[J]. Power System Technology, 2004, 28(7): 1-6, 18.

[15] 刘辉, 李啸骢, 韦化. 基于目标全息反馈的发电机非线性综合控制设计[J]. 中国电机工程学报, 2007, 27(4):21-25.LIU Hui, LI Xiao-cong, WEI Hua. Nonlinear integrated control design for generator unit based on NCOHF[J].Proceedings of the CSEE, 2007, 27(4): 21-25.

[16] 刘辉, 李啸骢, 韦化. 基于目标全息反馈法的发电机非线性励磁控制设计[J]. 中国电机工程学报, 2007,27(1): 14-18.LIU Hui, LI Xiao-cong, WEI Hua. Nonlinear excitation control for generator unit based on NCOHF[J].Proceedings of the CSEE, 2007, 27(1): 14-18.

[17] 刘辉, 李啸骢, 韦化. 基于目标全息反馈法的单输入多输出控制系统极点配置[J]. 中国电机工程学报,2008, 28(4): 59-64.LIU Hui, LI Xiao-cong, WEI Hua. Pole assignment of nonlinear control with objective holographic feedbacks for the single input multiple output controlled system[J].Proceedings of the CSEE, 2008, 28(4): 59-64.

[18] 刘辉, 李啸骢, 韦化. 大型汽轮发电机组目标全息反馈非线性综合控制设计[J]. 电工技术学报, 2008, 23(4):25-31.LIU Hui, LI Xiao-cong, WEI Hua. Nonlinear coordinated control with objective holographic feedbacks for large turbo-generator set[J]. Transactions of China Electrotechnical Society, 2008, 23(4): 25-31.

[19] 刘辉, 李啸骢, 韦化. 多输入控制系统中目标全息反馈法的极点配置原理[J]. 中国电机工程学报, 2008,28(7): 58-63.LIU Hui, LI Xiao-cong, WEI Hua. Pole assignment mechanism of nonlinear control with objective holographic feedbacks for the multiple-input controlled system[J]. Proceedings of the CSEE, 2008, 28(7): 58-63.

[20] 刘辉, 汪旎, 韦化, 等. 发电机组目标全息反馈大范围稳定控制设计[J]. 中国电机工程学报, 2008, 28(31):21-26.LIU Hui, WANG Ni, WEI Hua, et al. Global asymptotic stable coordinated control with objective holographic feedbacks for the turbo-generator set[J]. Proceedings of the CSEE, 2008, 28(31): 21-26.

[21] 卢强. 电力系统非线性控制[M]. 北京：科学出版社,2008: 123-168.