基于广域测量系统和归一化峰度在线检测电网扰动信号

邸 斌，徐玉韬

(1.哈尔滨理工大学电工电子教学与实训中心，黑龙江 哈尔滨 150040；2.贵州电力试验研究院，贵州 贵阳 550002）

0 引言

由同步相量测量单元（Phasor Measurement Unit,PMU）为基本单位组成的广域测量系统（Wide Area Measurement System, WAMS）的出现，为大规模互联电力系统的监视、分析和控制提供了新的手段[1-2]。电力系统发生故障后，WAMS/PMU信号中会出现扰动，基于WAMS/PMU信号的电网扰动在线检测是电力系统在线安全分析的基础性环节[3-4]。电网扰动的及时发现可以提示调度运行人员快速采取必要的控制措施，以防止故障范围的进一步扩大。扰动信号的特点是随机性强、持续时间短，目前尚无一个统一的检测方法和标准。常用扰动信号检测方法有：时域差分法、小波方法、模型差值法、突变量方法、数学形态学方法等。时域差分法[5]的优势在于算法原理及计算过程相对简单，在线应用之中占空比低，不足之处是差分结果的奇异性不高，在输电线路负荷水平波动较大的情况下，难以准确检测扰动信号的全过程，其计算结果可靠性有待商榷；小波方法[6-7]通过小波变换模极大值理论获取信号的突变点，较为准确地得到信号的时间定位，提高了扰动信号检测的精度，处理奇异信号的能力较强，在扰动信号检测领域应用广泛，母小波的选取是该方法关键因素，直接影响检测结果的精度，在线应用中存在一定的局限性；模型差值法[8]建模过程复杂、计算量大，在线应用之中占空比指标过高，限制了其实际应用价值；突变量方法[9]在扰动信号检测中应用广泛，但是不适宜大扰动信号的检测，这是由于大扰动信号随机波动大，导致阈值选取复杂，无法有效判断，故而也受到一定的局限；数学形态学方法通过“探针”收集信号的信息，利用“探针”与所检测信号进行匹配测试分析，达到扰动信号检测目的，目前已在电能质量扰动检测领域得到了一定的应用[10-11]，也有一些学者将其引入电网PMU信号的扰动检测领域[12]，但由于扰动阈值设定较为复杂，在线应用效果有待验证。

为了解决上述各种扰动信号检测方法在线应用难题，本文首次提出一种基于WAMS/PMU信号的归一化峰度（Normalization Kurtosis，记为xnk）指标，对电网扰动信号进行在线检测的方法。其原理是在对实测信号进行标准化处理后，基于滑动窗技术在线计算标准化信号的归一化峰度，将结果与扰动阈值对比，以实现扰动信号在线检测。该方法的最大特点是：扰动阈值设置容易（如设置为8）、计算简单、适合在线应用。IEEE-39节点系统时域仿真信号和电网实测信号分析表明：该方法计算量小，简单易行，能有效、可靠地对电网扰动信号在线检测，具有较高的工程在线实用价值。

1 广域测量信号及归一化峰度

1.1 广域测量信号

电力系统运行过程中，WAMS/PMU信号可分为两种[13-15]：1）稳态信号（Ambient Signal）。由系统稳态运行时，持续存在的负荷投切等随机性质小扰动因素引起，如图1(a)中0~633 s以及647~1 200 s所示。2）动态信号（Ringdown Signal）。由系统内某种短时大扰动引起，如图1(a)中634~646 s所示。

稳态和动态这两种信号均具有一定的随机特性，这两种信号的数值是不能先验确定的随机变量，但它们的数值常常服从某种统计规律，即，可以用概率密度分布特性进行描述。

1.2 基于归一化峰度判断信号类型

概率密度分布满足正态分布的信号为高斯（Gaussian）信号，否则为非高斯（Non-Gaussian）信号[16-17]。文献[17]指出：归一化峰度是区分高斯信号与非高斯信号的量化指标，归一化峰度等于 3的信号称为高斯信号，小于 3的信号称为亚高斯（Sub-Gaussian）信号，大于 3的信号称为超高斯（Super-Gaussian）信号。

对于N个数据{x(t)}，(t=1,2,…,N)，其归一化峰度xnk的计算公式为

式中：E表示求均值；E{x4(t)}表示对N个数据的4次方求均值；E2{x2(t)}表示对N个数据的平方求均值后再进行平方。

2 电网扰动在线检测方案

2.1 电网实测信号分类测试

取南方电网金换线实测有功功率信号（图1(a)）并进行标准化处理[14-15]（图1(b)），数据长度1 200 s，采样率5 Hz，其中0~633 s以及647~1 200 s为稳态数据，634~646 s为动态数据。按照1.1节WAMS/PMU信号的分类，分为稳态信号、动态信号和稳态动态混合信号（测试信号中同时包含稳态和动态信号）三种类型进行测试，结果见表1~表4。

表1、表2表明，稳态信号或动态信号的归一化峰度在3附近小幅波动；表3、表4表明，即使稳态信号与动态信号的比例不同，稳态动态混合信号的归一化峰度也均远远大于3。

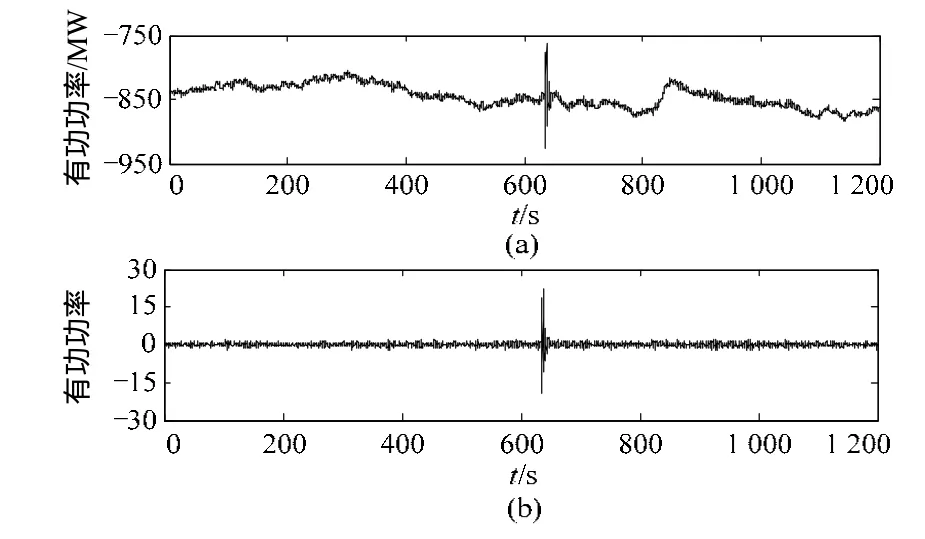
图1 实测及标准化有功功率Fig. 1 Measured and standardization of active power

表1 稳态信号归一化峰度Table 1 Normalization kurtosis of ambient signal

表2 动态信号归一化峰度Table 2 Normalization kurtosis of ringdown signal

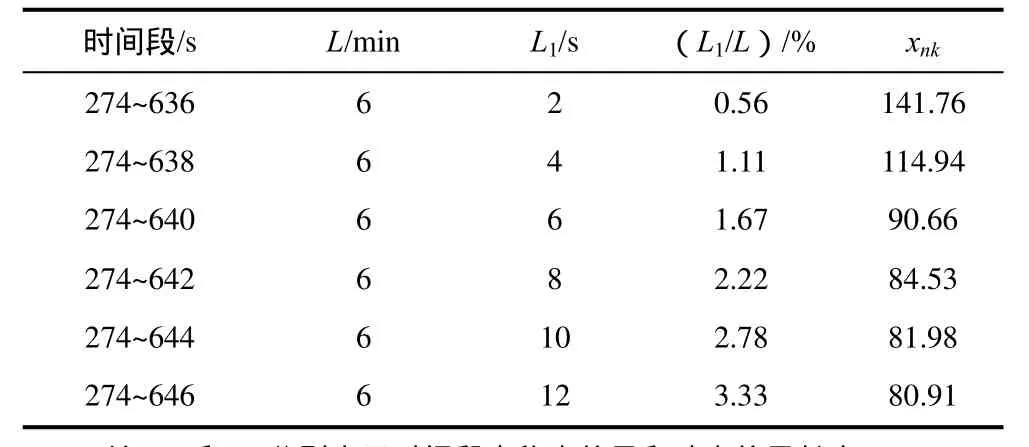
表3 稳态动态混合信号归一化峰度Table 3 Normalization kurtosis of mixed signal

表4 稳态动态混合信号归一化峰度Table 4 Normalization kurtosis of mixed signal

2.2 基于滑动窗技术的电网扰动信号检测流程

为满足xnk在线计算需求，采用滑动窗[18]技术。在完成限定数据窗内信号的xnk计算后，按照滑动步长更新信号，再计算更新后信号的xnk，如图2所示。

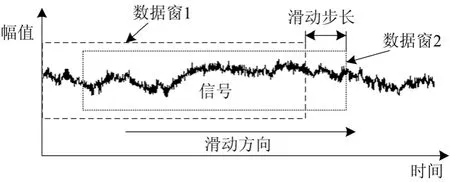
图2 滑动窗示意图Fig. 2 Sketch map of sliding window

基于上述分析，可以设计如图3所示的电网扰动信号在线检测方案，在线判断电网扰动信号情况。

图3 基于归一化峰度电网扰动信号在线检测方案Fig. 3 Scheme of online power system disturbance signal detecting based on normalization kurtosis

判断依据如下：

1）若xnk在3附近，表明没有扰动信号存在。

2）若xnk瞬间发生跳变（数值瞬间增大），表明扰动信号刚刚发生。

3）若 xnk远大于 3，表明扰动信号依然存在于当前滑动窗内。

4）若xnk再次恢复到3附近，表明扰动信号已经完全离开当前滑动窗。

3 IEEE-39节点系统仿真信号算例

采用Matlab的Power System Analysis Toolbox（PSAT）对IEEE-39节点测试系统（如图4所示）进行仿真测试。

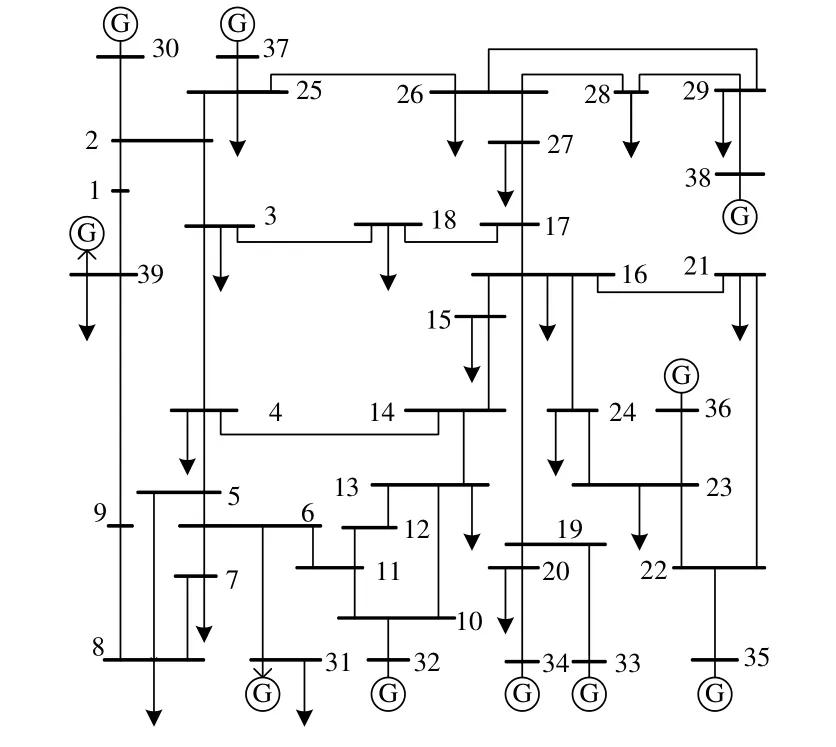
图4 IEEE-39节点测试系统Fig. 4 IEEE-39 bus test system

为获取仿真系统的稳态信号，需要模拟实际电力系统中的随机扰动，在仿真系统每个节点上注入高斯白噪声。

仿真时间长度1 200 s，信号采样率20 Hz，在600 s时断开节点1-2支路，1 s后恢复，获取节点8-9支路有功功率信号（图5(a)），然后标准化处理，将标准化信号（图5(b)）作为后续分析信号。

图5 8-9支路仿真及标准化有功功率数据Fig. 5 Simulation and standardization of active power of branch 8-9

3.1 20 Hz采样率信号测试分析

为分析不同长度的滑动窗以及滑动步长对 xnk计算结果的影响，对图5(b)信号设定不同长度的滑动窗和滑动步长进行测试。滑动窗取4 min滑动步长取4 s时、滑动窗取6 min滑动步长取6 s时和滑动窗取8 min滑动步长取8 s时的计算结果分别如图6(a)、图6(b)、图6(c)所示。图中xnk计算结果用“*”表示。

图6 20 Hz采样率信号归一化峰度Fig. 6 Normalization kurtosis of 20 Hz signal

图6 表明：当滑动窗内仅包含稳态信号时，xnk在3附近波动，当滑动窗内同时包含稳态动态混合信号时，xnk远大于3。

图6对比分析表明：当滑动窗内包含相同数量长度的扰动信号时，随着滑动窗口长度的增大，xnk逐渐增大，这和表4的分析结果一致。

3.2 降采样信号测试分析

为了分析不同采样率信号的 xnk测试结果，对仿真信号降采样后用同样方法测试分析。图 7(a)、图7(b)给出了5 Hz采样率信号在滑动窗取6 min滑动步长取6 s时和滑动窗取8 min滑动步长取8 s时的测试结果。

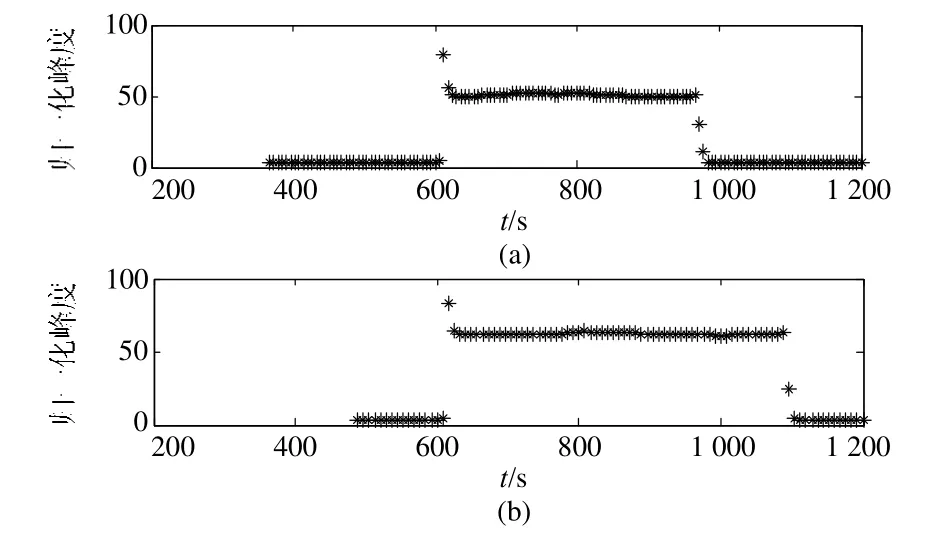
图7 5 Hz采样率信号归一化峰度Fig. 7 Normalization kurtosis of 5 Hz signal

降采样信号测试结果同样验证了图6分析得到的结论。对图6和图7的部分测试结果进行统计分析，见表5。

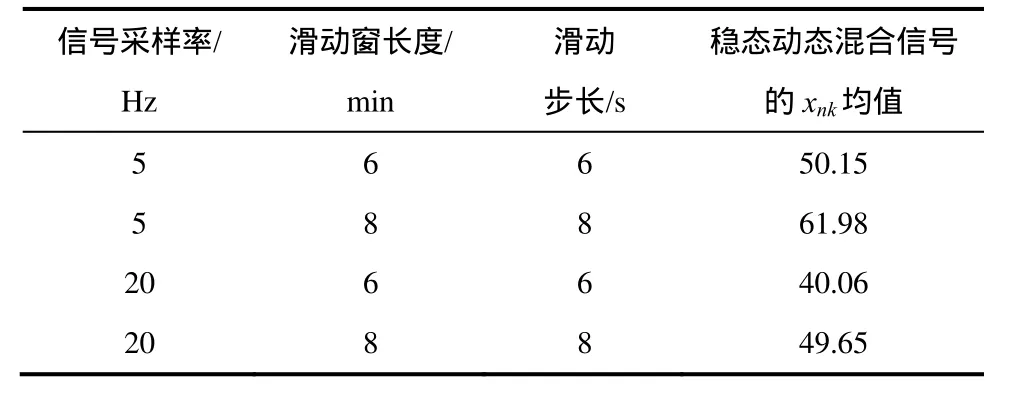
表5 归一化峰度统计结果Table 5 Statistical result of normalization kurtosis

表5表明：1）信号采样率相同时，滑动窗口和滑动步长的长度越大，稳态动态混合信号的 xnk均值越大；2）滑动窗口和滑动步长的长度相同时，信号采样率越低，稳态动态混合信号xnk均值越大。

因此，电网扰动信号在线检测的工程实际应用中，应适当增大滑动窗的长度以保证扰动阈值的可靠性，充分保证电网扰动信号在线检测的准确性。

4 电网实测信号算例

取南方电网罗马线实测有功功率信号（如图 8所示）进行测试，数据长度1 200 s，采样率5 Hz。滑动窗取4 min滑动步长取4 s时、滑动窗取6 min滑动步长取6 s时和滑动窗取8 min滑动步长取8 s时的计算结果分别如图9所示。

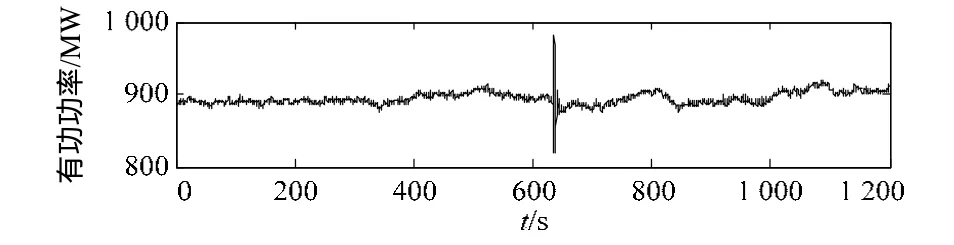
图8 实测有功功率Fig. 8 Measured active power

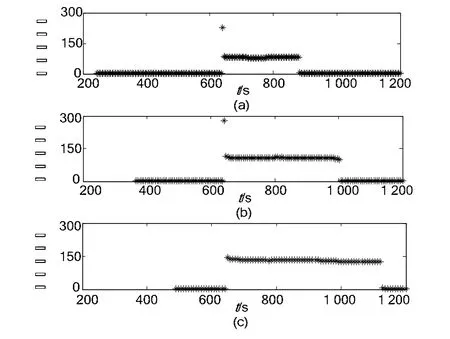
图9 实测信号的归一化峰度Fig. 9 Normalization kurtosis of measured signal

图9表明：在滑动窗长度取值不同的情况下，本文方法均可准确判断电网中是否存在扰动信号。验证了本文提出的电网扰动信号在线检测方法的可行性和可靠性。xnk测试情况的统计分析结果见表6。

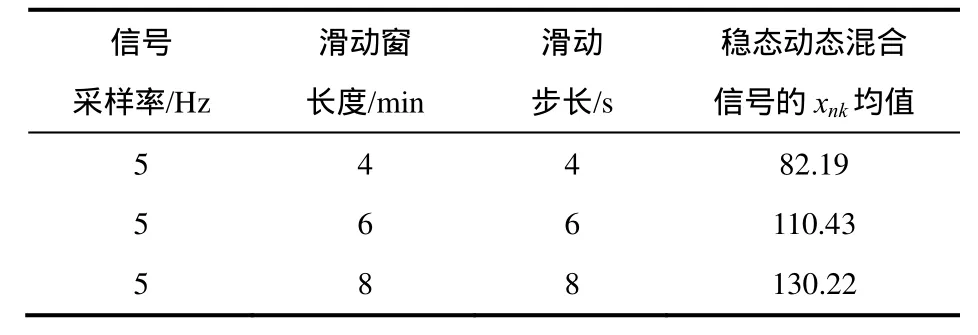
表6 归一化峰度统计结果Table 6 Statistical result of normalization kurtosis

表6同样表明：应适当增大滑动窗的长度，以充分保证电网扰动信号在线检测的可靠性。

对图8中的扰动信号的幅值进行弱化处理，结果如图10所示。再用同样的方法检测相对较弱的扰动信号，检测结果见图11。

图11表明：对相对较弱的扰动信号，本文方法依然可准确及时地进行检测。

图10 降幅值实测有功功率Fig. 10 Reduced amplitude of measured active power

图11 实测信号的归一化峰度Fig. 11 Normalization kurtosis of measured signal

5 结论

本文从信号概率分布统计特性出发，将WAMS/PMU实测信号分为稳态信号、动态信号以及稳态动态混合信号三种情况，细化测试分析了这三种不同类型信号的归一化峰度指标，得到了“稳态信号或动态信号的归一化峰度接近于 3，为近似高斯信号；稳态动态混合信号的归一化峰度远远大于3，为超高斯信号”的结论。

基于上述结论，结合滑动窗技术，提出了一种基于实测信号归一化峰度指标的电网扰动信号在线检测方法，时域仿真算例和电网实测信号算例分析表明该方法具有普遍适用、简单有效、计算量小、扰动阈值容易设置等一系列优点，非常适用于在线应用，具有较高的工程实用价值。

[1] 周喜超, 智勇, 郑伟, 等. 基于 WAMS系统的甘肃陇南电网大负荷扰动试验[J]. 电力系统保护与控制,2010, 38(12): 129-131.ZHOU Xi-chao, ZHI Yong, ZHENG Wei, et al. Large load disturbance based on WAMS in Longnan of Gansu power grid[J]. Power System Protection and Control,2010, 38(12): 129-131.

[2] 王波, 陆进军. 基于同步相量测量技术的励磁系统调节性能分析方法及其系统实现[J]. 电力系统保护与控制, 2012, 40(3): 135-140.WANG Bo, LU Jin-jun. A method for analyzing the regulating performance of excitation system based on synchronized phasor measurement technology and its system realization[J]. Power System Protection and Control, 2012, 40(3): 135-140.

[3] 干磊, 康河文, 何敏. 基于广域测量系统的电压稳定动态监测[J]. 电力系统保护与控制, 2010, 38(21):152-155.GAN Lei, KANG He-wen, HE Min. The dynamic monitoring of voltage stability based on wide-area measurement system[J]. Power System Protection and Control, 2010, 38(21): 152-155.

[4] 秦晓辉, 毕天枢, 杨奇逊. 基于广域同步量测的电力系统扰动识别与定位方法[J]. 电网技术, 2009, 33(12):35-41.QIN Xiao-hui, BI Tian-shu, YANG Qi-xun. WAMS based power system disturbance identification and location approach[J]. Power System Technology, 2009, 33(12):35-41.

[5] 魏磊, 张伏生, 耿中行, 等. 基于瞬时无功功率理论的电能质量扰动检测[J]. 电网技术, 2004, 28(6): 53-58.WEI Lei, ZHANG Fu-sheng, GENG Zhong-xing, et al.Detection, location and identification power quality disturbance based on instantaneous reactive power theory[J]. Power System Technology, 2004, 28(6): 53-58.

[6] 储珺, 马建伟. 基于小波变换的电能质量扰动信号的检测[J]. 电力系统保护与控制, 2009, 37(5): 34-36.CHU Jun, MA Jian-wei. Detection of power quality disturbed signal based on wavelet transform[J]. Power System Protection and Control, 2009, 37(5): 34-36.

[7] 胡国胜, 朱锋峰, 任霞. 电能扰动检测和识别线调频三角样条小波方法[J]. 继电器, 2006, 34(2): 46-52.HU Guo-sheng, ZHU Feng-feng, REN Xia. Power quality disturbance detection and identification using chirplet transform with trigonometric spline kernels[J].Relay, 2006, 34(2): 46-52.

[8] GuI Y H, Styvaktakis E, Bollen M H J. Analyzing power disturbances using the residuals of AR models[J]. IEEE Power Engineering Review, 2000, 20(4): 60-62.

[9] 倪广魁, 鲍海, 张利, 等. 基于零序电流突变量的配电网单相故障带电定位判据[J]. 中国电机工程学报,2010, 30(31): 118-122.NI Guang-kui, BAO Hai, ZHANG Li, et al. Criterion based on the fault component of zero sequence current for online fault location of single-phase fault in distribution network[J]. Proceedings of the CSEE, 2010,30(31): 118-122.

[10] 王丽霞, 何正友, 赵静, 等. 小波变换和数学形态学在电力扰动信号消噪中的应用[J]. 电力系统保护与控制,2008, 36(24): 30-35.WANG Li-xia, HE Zheng-you, ZHAO Jing, et al.Wavelet transform and mathematical morphology’s application in power disturbance signal denosing[J].Power System Protection and Control, 2008, 36(24):30-35.

[11] 李庚银, 罗艳, 周明, 等. 基于数学形态学和网格分形的电能质量扰动检测及定位[J]. 中国电机工程学报,2006, 26(3): 25-30.LI Geng-yin, LUO Yan, ZHOU Ming, et al. Power quality disturbance detection and location based on mathematical morphology and grille fractal[J].Proceedings of the CSEE, 2006, 26(3): 25-30.

[12] 何潜, 陈刚, 王予疆, 等. 基于数学形态学的电网PMU信号的扰动检测方法[J]. 华东电力, 2012, 40(2):211-215.HE Qian, CHEN Gang, WANG Yu-jiang, et al.Disturbance detection approach from power system PMU data based on mathematical morphology[J]. East China Electric Power, 2012, 40(2): 211-215.

[13] Zhou N, Pierre J W, Trudnowski D J, et al. Robust RLS methods for online estimation of power system electromechanical modes[J]. IEEE Trans on Power Systems, 2007, 22(3): 1240-1249.

[14] 吴超, 陆超, 韩英铎, 等. Prony方法和ARMA法在低频振荡模式辨识中的适用性比较[J]. 电力自动化设备,2010, 30(3): 30-34.WU Chao, LU Chao, HAN Ying-duo, et al. Comparison of applicability in low frequency oscillation mode identification between Prony and ARMA[J]. Electric Power Automation Equipment, 2010, 30(3): 30-34.

[15] 徐玉韬, 卢继平, 陈刚, 等. 稳态和动态混合信号的在线低频振荡模式辨识方法[J]. 电力系统自动化, 2012,36(2): 31-35, 105.XU Yu-tao, LU Ji-ping, CHEN Gang, et al. An online low frequency oscillation estimation method for ringdown signals mixed ambient ones[J]. Automation of Electric Power Systems, 2012, 36(2): 31-35, 105.

[16] 邱天爽, 张旭秀, 李小兵, 等. 统计信号处理——非高斯信号处理及其应用[M]. 北京: 电子工业出版社,2004.

[17] 张贤达. 现代信号处理[M]. 2版. 北京: 清华大学出版社, 2002.

[18] 陈刚, 段晓, 张继红, 等. 基于 ARMA 模型的低频振荡模式在线辨识技术研究[J]. 电网技术, 2010, 34(11):48-54.CHEN Gang, DUAN Xiao, ZHANG Ji-hong, et al. A new approach for online identification of low frequency oscillation modes based on auto-regressive movingaverage model[J]. Power System Technology, 2010,34(11): 48-54.