一种带有奖惩参数的动态因子分析综合评价法

李 莉

(宁夏大学数学计算机学院，银川750000)

因子分析方法最早是在1904年由Charles Spearman和Karl Pearson提出，它的基本思想是将实测的多个指标，用少数几个潜在的指标的线性组合来表示［1］.因子分析的主要应用有两个方面，一是寻求基本结构，简化观测系统;二是对变量或样本进行分类.目前它可以应用于心理学、社会学、经济学、人口学、地质学、生理学、环境学等多个研究领域［2-4］.很多统计软件如SPSS，SAS等都带有因子分析功能.但是由于利用因子分析法进行综合评价时，只是使用了当期的截面数据，并没有考虑上一期数据的影响，因此该综合评价方法是静态的［5］.本文引入了一种具有奖惩参数的动态因子分析综合评价法，此法不仅综合了传统因子分析法的结果，而且考虑到了系统在不同时期的动态关联性.

1 传统的因子分析综合评价法

1.1 因子分析法的基本数学原理

因子分析法的核心思想是降维，即把多个指标转化为少数几个相互独立的综合指标，用较少的因子来反映原有数据的绝大部分信息.具体可用数学模型来表示.设原有n个变量x=(x1，x2，…，xn)T，将每个原有的变量用m(m ＜n)个公共因子f1，f2，…，fm的线性组合来表示，即

简记为x=Af+ε.

其中:aij(i=1，2，…，n;j=1，2，…，m)为因子荷载;εi(i=1，2，…，n)为特殊因子，均值为0，相互独立，表示原有变量不能被解释的部分.因子荷载aij表示第i个变量在第j个主因子上的荷载，即第i个变量与第j个因子的相关系数.荷载越大说明第i个变量与第j个因子的关系越密切;荷载越小说明第i个变量与第j个因子的关系越疏远.公共因子f1，f2，…，fm是在各个变量中共同出现的因子，在高维空间中，它们是相互垂直的坐标轴.特殊因子εi(i=1，2，…，n)实际上就是观测变量与估计值之间的残差值.为了使找到的主因子更易于解释，通常需要对因子荷载矩阵进行旋转.旋转的方法很多，使用比较多的是最大方差旋转法.进行因子旋转的目的就是要使因子荷载矩阵中因子荷载的平方值向0和1两个方向分化，使大的荷载更大，使小的荷载更小.将因子表示为变量的线性组合式，所得到的计算结果称为因子得分，它是对公共因子的估计值，利用它，可以对实际问题作进一步的分析.

使用SPSS17.0软件可求出因子得分函数

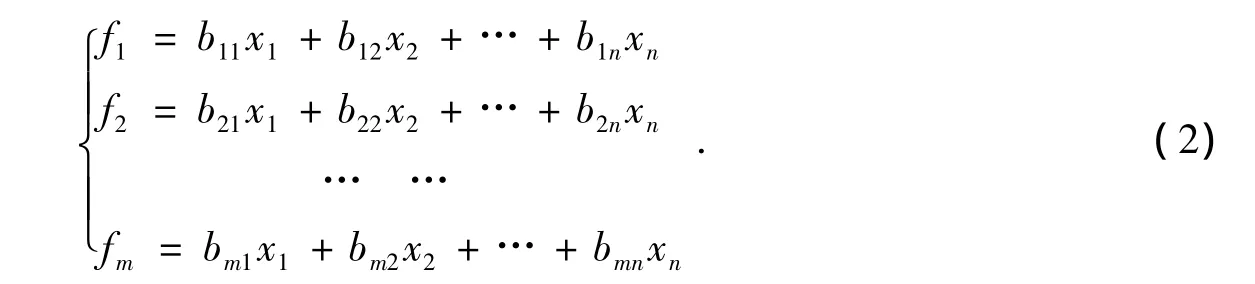
1.2 传统的因子分析综合评价法的原理

传统的因子分析评价法的核心就是通过因子分析法，选取m个主因子f1，f2，…，fm，以每个主因子的方差贡献率作为权重，构造综合评价函数:

把m个因子得分代入(3)式，算出综合得分，最后利用综合得分来进行综合评价.

具体步骤如下:

第一步，对原始的数据进行标准化处理:

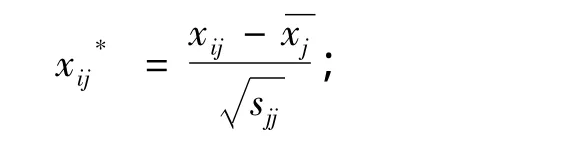
第二步，对已标准化的数据进行因子提取;

第三步，选用最大方差旋转法对因子荷载矩阵进行旋转，得到旋转因子得分矩阵，从而代入到(3)式求出综合因子得分来进行综合评价.

使用因子分析法进行综合评价在很多领域都有着广泛的应用，但是此法有一定的局限性.因为它只是基于当期的数据，而没有考虑到不同时刻系统的动态关联性.因此，本文将提出一种动态因子分析综合评价法来弥补这一缺陷.

2 动态因子分析综合评价法

动态因子分析综合评价法里用到了一个新的概念:因子分析排序指数，下面给出其定义.

2.1 因子分析排序指数定义

称 Wik=Fi，k+ λ(Fi，k-Fi，k-1)(其中 i=1，2，…，n;k=2，3，…，N;0 ≤ λ ≤ 1) (4)为系统Ai在tk时刻的具有奖惩效果的因子分析排序指数，式中的λ为奖惩参数，Fi，k，Fi，k-1分别为系统si在tk，tk-1时刻的综合因子得分.

根据定义可知，因子分析排序指数是该时刻综合因子得分与该时刻综合因子得分改变量的加权和.特别地，当λ=0时，既无激励也无惩罚，因子分析排序指数即是综合因子得分.此时，动态因子分析评价法就等同于传统的因子分析评价法.一般情况下，λ的取值范围应该在0到1之间.λ取值越小，则激励或惩罚的程度就会越小;λ取值越大，则激励或惩罚的程度就会越大.在实际的问题中，λ的取值就显得尤为重要，既不能太大，也不能太小.λ取值太大，就会出现奖惩过度的情况，λ取值太小就会起不到应有的激励效果.

2.2 参数λ的确定方法

奖惩参数λ的取值可按以下两种方法来确定.

2.2.1 专家打分法

专家打分法就是根据多位专家就系统的运行状况打分来确定λ.但此方法具有较强的主观性.

2.2.2 相关系数法

相关系数法即根据系统Ai变化的情况来确定λ的取值.具体做法如下:以Ci，k表示系统Ai在tk时刻按综合因子得分排序的位次，以Ci，k-1表示系统Ai在tk-1时刻按综合因子得分排序的位次;以Fi，k表示系统Ai在tk时刻的综合因子得分，Fi，k-1表示系统Ai在tk-1时刻的综合因子得分.同一个系统在不同时刻的综合因子得分不同，则排名位次有可能不同.这是因为排名的结果，不仅依赖于系统本身的变化，还依赖于其他系统的变化情况.奖惩参数的设计就是考虑到激励的目的，综合因子得分增加的越大，则激励就应该越大.于是，自然想到以综合因子得分的改变量与排名位次改变量的相关系数来衡量有效激励λ，因此，λ的确定公式为:

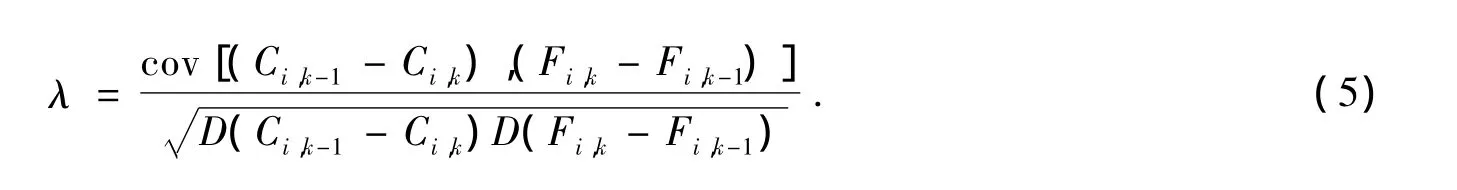
2.3 具体做法

在使用这种动态因子综合评价方法时，首先要确定奖惩参数λ的值，一般使用公式(5)即相关系数法来确定.我们可以借助SPSS17.0软件计算出n个系统Ai(i=1，2，…，n)在两个时刻tk，tk-1的综合因子得分 Fi，k，Fi，k-1和在这两个时刻按综合因子得分排序的位次 Ci，k，Ci，k-1.确定了 λ 的值后代入公式(4)中确定出各系统Ai(i=1，2，…，n)的因子分析排序指数Wi，k(i=1，2，…，n).那么我们在时刻tk对各系统就可以依据Wi，k(i=1，2，…，n)的取值大小排序从而进行综合评价.

3 结语

这种带有奖惩参数的动态因子综合评价法与原有静态的因子分析法相比较，评价的可靠性要更高一些，因为它不仅考虑了系统当前的截面数据，还把系统在前一时刻的状况也考虑了进去.如果需要经常性地对某些系统进行综合评价时，这种评价方法尤其适用.因为它的这种奖惩的效果会使得评价的可靠性和有效性更好一些.在使用该方法进行综合评价时，奖惩参数λ的确定尤为关键，一般使用第二种相关系数法来确定更为客观一些.

［1］范金城，梅长林.数据分析［M］.北京:科学出版社，2002.

［2］陈希镇，林俊涛.用多元统计方法分析浙江省各地区的经济结构［J］.数理统计与管理，2010，29(6):1043-1051.

［3］吴建民，丁疆辉.基于因子分析模型的河北省县域发展空间差异的研究［J］.河北师范大学学报，2010，34(6):739-744.

［4］战英杰，申秋红.影响我国农民收入的因子分析［J］.东北农业大学学报，2010，41(4):144-150.

［5］郭亚军.综合评价理论、方法及应用［M］.北京:科学出版社，2007.