齿轮啮合冲击过程分析及评价方法

康 焱，石照耀

(1. 北京工业大学机械工程与应用电子技术学院，北京 100124；2. 中国空间技术研究院载人航天总体部，北京 100094)

齿轮啮合冲击过程分析及评价方法

康 焱1,2，石照耀1

(1. 北京工业大学机械工程与应用电子技术学院，北京 100124；2. 中国空间技术研究院载人航天总体部，北京 100094)

基于我国首创的齿轮整体误差测量技术，以笔者提出的齿轮副整体误差为手段，从微观上解释了齿轮啮合冲击产生的具体过程，归纳了轮齿交替特性，提出了一种以轮齿交替特性为评价准则的齿轮啮合冲击的评价方法；总结了6种基本的交替形式，给出了各自的判别准则，统一了齿面交替和顶刃交替的判别方法，讨论了各交替形式与啮合冲击的关系；最后，以上述理论为基础，开发了齿轮啮合冲击测评系统并给出了分析实例．研究结果表明，齿轮副整体误差是研究齿轮啮合冲击问题的一种有效工具，以轮齿交替特性为基础的统计学评价方法为批量齿轮啮合冲击的测评和预报提供了一种新的方法和途径．

齿轮；啮合冲击；齿轮噪声；齿轮副整体误差

齿轮啮合冲击是齿轮传动中经常存在的一种现象[1]，产生机理非常复杂，迄今任何一种数学模型都难以对其进行全面表征[2]．

啮合冲击是齿轮传动噪声的主要激励源之一[3]．对于啮合冲击引起的冲击力、冲击噪声的计算和评价，以前的研究主要集中在通过啮合冲击点(啮入撞击点和啮出撞击点)的几何位置判据，来分析计算引起的冲击速度、冲击力和冲击能量[4-5]，进而探讨传动比、模数等对啮合冲击的影响[6-7]．不仅计算过程复杂，而且在计算中一般只能计算出啮合起始点处的冲击能量．而在实际中，每对轮齿在交替中会出现多次交替，产生多次啮合冲击[8-9]．

齿轮副整体误差(gear pair integrated error，GPIE)[10]以我国首创的齿轮整体误差测量技术[11]为基础，根据误差作用原理和机构精度理论而合成得到，目的是为克服齿轮传动误差在研究齿轮动态特性和振动噪声时的不足[12]．GPIE曲线与传动误差曲线相比，它包含的误差信息更全面，不仅反映了啮合过程中主从动轮误差相互作用的结果[13]，其外包络线也代表了该对齿轮副的静态传动误差曲线，更重要的是反映了每对轮齿的完整啮合过程，包括顶刃啮合过程[14]．

笔者用GPIE来研究和评价齿轮啮合冲击，不仅可以直观地认识啮合冲击的具体产生过程，而且可以分析计算出两对轮齿在每次交替啮合时引起的啮合冲击．通过GPIE曲线可以更深入地研究啮合冲击和齿轮误差的关系，更准确地评价齿轮在交替啮合过程中的啮合冲击情况．

1 啮合冲击的产生过程

在齿轮实际啮合过程中，由于加工误差、弹性变形及其各种啮合干扰的影响，使得相邻两对轮齿在交替中会出现多次交替现象，齿轮啮合冲击就是轮齿在这种多次交替过程中引起的轮齿反复撞击．

定义齿轮副啮合齿距偏差为

式中：pb1()ft和pb2()ft分别为主、从动轮的基圆齿距偏差；1()tδ和2()tδ分别为主、从动轮受载后沿啮合线方向的弹性变形．变形使得主动轮进入啮合时的齿距偏差减少，从动轮的齿距偏差增大．

啮合冲击的产生条件为

如果将齿轮的啮合冲击与啮合过程相对应，那么一对轮齿的传动过程最多可能包括5个阶段[10-11]．

(1) 啮入撞击．如图1所示，当pb0F＞时，前对轮齿尚未啮合到第2个双啮区的起点0G，后一对轮齿的从动轮齿顶就提前在啮合线外的1G点进入啮合．在1G点，从动轮的转速突然上升，从动轮的齿顶棱边撞击在主动轮的轮齿根部，称为啮入撞击．图2(a)所示GPIE曲线上的jG1,+1为后一对轮齿1j+的啮入撞击点．

(2) 从动轮顶刃啮合．当存在啮入撞击时，自提前啮入点1G到理论啮合起点1B(如图1所示)，从动轮的顶刃在主动轮的齿根刮行，称为从动轮顶刃啮合．这期间可能产生脱齿和脱齿后的轮齿撞击，图2(a)所示的从点1,1jG+到点1,1jB+为后一对轮齿1j+的从动轮顶刃啮合对应的GPIE曲线．

图1 啮合冲击的产生过程Fig.1 Emerging process of meshing impact

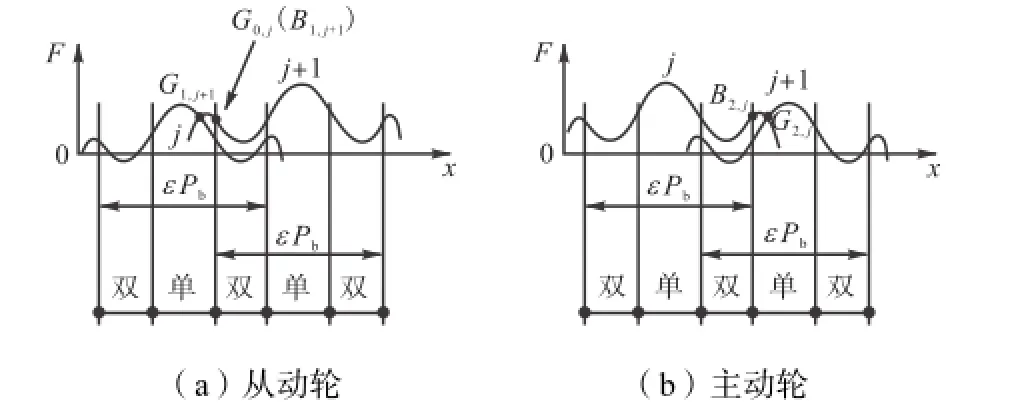
图2 啮合冲击产生过程对应的GPIE曲线Fig.2 GPIE curves of emerging process of meshing impact

(3) 渐开线齿廓啮合．主、从动轮齿廓沿理论啮合线方向的啮合，即渐开线齿廓啮合．在这个过程中，主要存在节点冲击．

(4) 主动轮顶刃啮合．当pb0F＜时，在前一对轮齿应该脱离啮合时，由于存在负的齿轮副啮合齿距偏差，后一对齿不能进入啮合，使得在前一对齿中，主动轮的齿顶就在被动轮齿根处向齿顶方向刮行，称为主动轮顶刃啮合．图1所示的理论啮合终点2B到实际啮出点2G为前一对轮齿j的主动轮顶刃啮合过程，对应的GPIE曲线如图2(b)所示的点2,jB到点2,jG．

(5) 啮出撞击．如图1所示，在主动轮顶刃啮合到2G点，这对轮齿就退出啮合，在下一对齿进入啮合的瞬间，由于存在法向速度差，下一对轮齿将发生碰撞而引起噪声，称为啮出撞击．图2(a)所示GPIE曲线上的2,jG点为前一对轮齿j的啮出撞击点．

2 轮齿的交替特性

图3为实际测量得到的GPIE曲线．由图3可以看出，从前一对轮齿过渡到后一对轮齿的误差曲线不是光滑过渡和连续变化，而是相互搭接的，这种搭接情况反映了轮齿交替啮合的具体过程，搭接点代表了轮齿间的交替点，前后两条误差曲线之间有几个搭接点就代表交替几次．

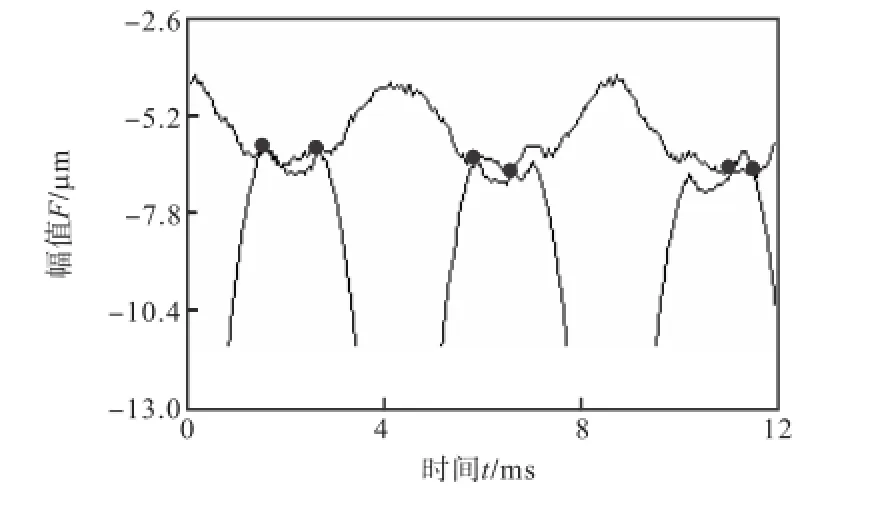
图3 GPIE曲线Fig.3 GPIE curves

相邻两对轮齿发生交替的条件是前后两对轮齿的GPIE曲线有搭接点，即

式中：Fj(t)为前一对轮齿j在t时刻的GPIE；Fj+1(t )为后一对轮齿j+1在t时刻的GPIE．

一般情况下，不同齿对的GPIE曲线之间的搭接情况都不同，反映了不同的交替过程．研究GPIE曲线的这些特点，由此提出了轮齿交替特性的概念．轮齿交替特性包括3个方面．

2.1 交替部位

交替部位是指交替点在轮齿上的具体位置，如齿顶、齿根及齿面．GPIE曲线上搭接点的位置就代表了轮齿交替的部位．不同的交替部位引起的啮合冲击类型有所不同．

2.2 交替次数

在一对轮齿的双啮区会出现多次交替，产生多次啮合冲击．交替次数是用来统计轮齿在交替过程中产生啮合冲击的次数，它决定了啮合冲击频率的高低，直接影响啮合冲击噪声的大小．

啮合冲击次数的统计原则为

式中Dτ为齿轮副在完整啮合周期上的总交替次数，反映了齿轮副在全部交替过程中产生的啮合冲击的次数．控制GPIE曲线上搭接点的个数就可以控制交替过程中引起冲击的次数．

式中：1z为主动轮的齿数；1N为齿轮副一个完整啮合周期内主动轮的转数．

2.3 齿对交替角

把在GPIE曲线上搭接点处，从前对轮齿GPIE曲线的切线逆时针转到后一对轮齿GPIE曲线的切线的夹角定义为齿对交替角(简称交替角)，用αD表示，如图4所示，0≤αD≤180°．它直观地表示了在每个交替点处由前一对轮齿交替到后一对轮齿时引起的齿轮传动速度的变化量，反映了该交替过程中引起的啮合冲击的轻重程度．

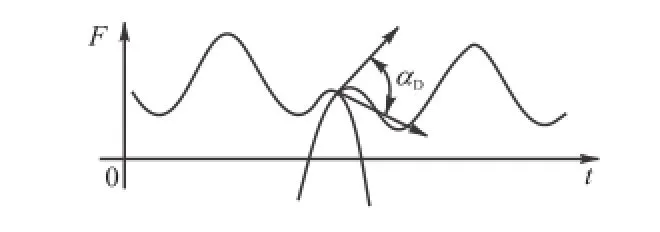
图4 齿对交替角的定义Fig.4 Teeth transition angle

当平稳交替时，如图5(a)所示，从前一对轮齿交替到后一对轮齿时没有突变点，角速度和角加速度均匀变化，交替平稳，不存在啮合冲击，此时，交替角αD=0．当为理想的渐开线齿轮时，GPIE曲线为一条直线，从一对齿交替到另一对齿时过渡平稳，没有引起啮合冲击，齿对交替角αD=0．

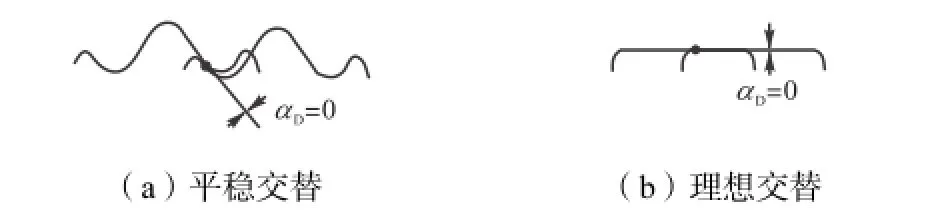
图5 特殊交替形式下的交替角Fig.5 Transition angles under special transition circumstance

为了统计齿轮副在完整啮合周期上的全部轮齿在交替啮合过程中引起的啮合冲击的轻重程度，引入交替角的均方根和一次交替过程中最大累计值αDmax，其中

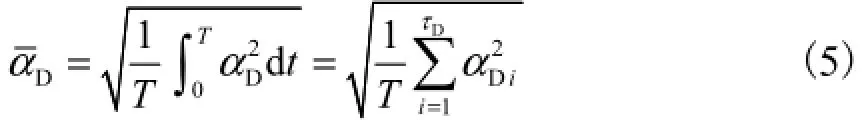
啮合冲击轻重程度的统计量原则为

3 基本交替形式

3.1 各交替形式的特点及其判别准则

根据轮齿交替形式引起的啮合冲击类型的不同，可以把轮齿的交替形式分为6种基本类型，如表1所示．表1中齿轮副的单啮区和双啮区为理论单、双啮区，对应的啮合线长度为理论值bPε(ε为重合度).

设iP为前一对轮齿j和后一对轮齿1j+的交替点，如图6所示，把以交替点iP为中心的任意开区间(iPσ+，iPσ-)称为交替点iP的交替邻域，记作U(Pi,σ)，σ称为该交替邻域的半径．当σ→0时，U(Pi,σ)称为交替点Pi的微小交替邻域．

当前后两对轮齿为齿面交替(如图6所示)时，在交替点Pi的微小交替邻域内，前一对轮齿j和后一对轮齿j+1的GPIE的差就是前面定义的齿轮副啮合齿距偏差．

表1 6种典型交替形式及其特例Tab.1 Six fundamental types of teeth transition process

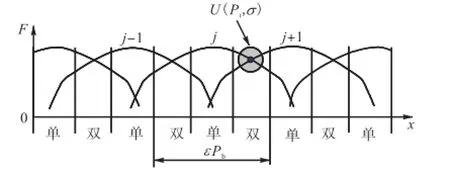
图6 交替点iP的交替邻域Fig.6 Teeth transition neighborhood on transition pointiP

当前后两对轮齿为顶刃啮合时，在顶刃交替点附近的GPIE曲线上，前一对轮齿j和后一对轮齿1j+的GPIE也有差值，但它不是齿轮副啮合齿距偏差．因为顶刃啮合段的GPIE曲线表示的是一个齿轮的齿顶棱边在另一个齿轮齿面上的刮行过程．把在顶刃交替点iP的微小交替邻域内，前一对轮齿j和后一对轮齿1j+的GPIE之差称为边缘齿轮副啮合齿距偏差，即

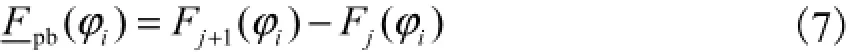
式中：iφ∈顶刃啮合区；为边缘齿轮副啮合齿距偏差．

在任意一对轮齿j的GPIE曲线上，理论单、双啮区对应的啮合线上的长度为εPb，顶刃啮合一定发生在该对轮齿的理论单、双啮区以外(如图6的εPb范围之外)，即发生在与它相邻的轮齿j-1或j+1的单啮区中．可见，对整个齿轮副而言，交替点Pi可能在双啮区，也可能在单啮区．当φi∈双啮合区时，Pi(φi)属于齿面交替；当φi∈单啮合区时，Pi(φi)属于顶刃交替．

在判断某个交替点Pi(φi)属于上述6种典型交替形式的哪一种之前，首先根据φi值属于单啮区还是双啮区，来判断使用Fpb(φ)还是(φi)作为判据．

第Ⅰ种交替类型是一种理想的交替形式，标准齿轮副的交替形式属于这种情况．但是在目前的齿轮加工制造水平下，不可能把齿轮加工到理想的程度．因此，第Ⅰ种交替形式在实际中不存在．

在交替点Pi的微小交替邻域内，若Fpb(φ)≡0，则Pi点属于第Ⅱ种交替类型，即平稳交替．重载齿轮副的交替形式多属于这种情况．

在交替点iP的微小交替邻域内，若pb()Fφ由负值变为正值，即pb()Fφ-→+由，则iP点属于第Ⅲ种交替类型，即齿面交替．从动轮为中鼓齿廓的齿轮副(主动轮为标准齿轮)的交替形式属于这种情况，这类齿轮副没有顶刃啮合，啮合工作主要由轮齿腹部来承担，齿对交替发生在齿廓上的某点．

在交替点Pi的微小交替邻域内，由负值变为正值，即由-→+，则Pi点属于第Ⅳ种交替类型，即降速交替．从动轮为负齿距偏差的齿轮副(主动轮为标准齿轮)的交替形式属于这种情况．

在交替点Pi的微小交替邻域内，由正值变为负值，即由+→-，则Pi点属于第Ⅴ种交替类型，即增速交替．从动轮为正齿距偏差的齿轮副(主动轮为标准齿轮)的交替形式属于这种情况．

在交替点Pi的微小交替邻域内，若pb()Fφ由正值变为负值，即pb()Fφ-→+由，则在iP点前后一定还存在顶刃交替，属于第Ⅵ种交替类型，即多次交替.从动轮为中凹齿廓的齿轮副(主动轮为标准齿轮)的交替形式属于这种情况．在多次交替中，既有齿面交替，又有顶刃交替；既有啮入时的从动轮顶刃啮合，又有啮出时的主动轮顶刃啮合．事实上，它由Ⅲ、Ⅳ和Ⅴ这3种交替形式组合而成，有至少3个交替点存在．

关于齿轮的交替特性需要补充2点．

(1) 同一对齿轮副上每对轮齿的交替特性有时往往具有相似性，这主要与齿轮的加工方法有关．例如：当采用未经修形的剃齿刀剃削齿数较少的齿轮时，常常产生中凹齿形齿廓[11]，这类型轮齿的交替形式多为第Ⅵ种交替类型．

(2) 有些齿轮副上各对轮齿的交替特性会表现出很大的差异性．例如：滚齿机加工齿数较多的齿轮时，会出现齿轮圆周上不同部段的齿廓误差变化很大，有的齿为中凸齿廓，对应的交替形式属于第Ⅲ种；有的齿为中凹齿廓，对应于第Ⅵ种交替形式；有的齿具有正压力角，对应于第Ⅳ种交替形式．

3.2 各交替形式与啮合冲击的关系

图7分别为后4种典型交替形式对应的GPIE曲线、角速度误差曲线和角加速度误差曲线．

从图7(a)可知，在齿面交替中，虽然在交替点处存在角速度的突变，但在交替过程中角速度变化缓慢，由此引起的角加速度较小，而且交替部位在齿腹，换齿时产生撞击而引起的动载荷不大．因此，齿面交替产生的啮合冲击较小．

发生降速交替时，从图7(b)可知，在交替过程中，首先是主动轮的顶刃在从动轮的齿面上刮行而造成轮齿顶刃啮合，使得从动轮逐渐减速，然后在交替点处发生啮出撞击而引起较大的噪声，且顶刃啮合发生在前一对齿上，而啮出撞击发生在后一对齿上．

发生增速交替时，从图7(c)可知，在交替过程中，首先在交替点处发生啮入撞击而引起强烈的噪声，从动轮转速急剧增加，然后从动轮的顶刃在主动轮的齿面上刮行而造成轮齿顶刃啮合，且啮入撞击和顶刃啮合发生在同一对轮齿上．这种交替产生的啮合冲击比降速交替要大得多．

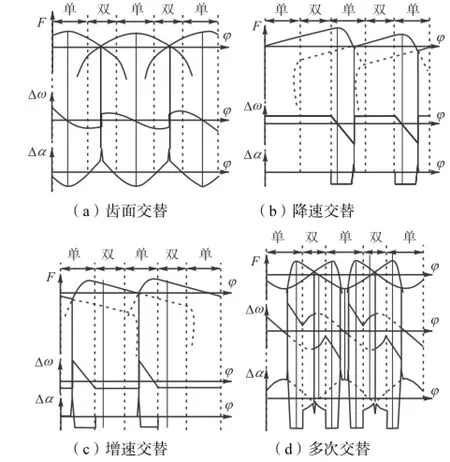
图7 各交替形式的GPIE曲线、角速度误差曲线和角加速度误差曲线Fig.7 GPEI curvs，angular speed curves and angular acceleration curves of teeth transitions

从图7(d)可知，在多次交替过程中，首先进行降速交替，然后进行齿面交替，最后进行增速交替．这种交替形式对传动质量的影响最坏，因为在前后两对轮齿的交替过程中，GPIE曲线发生多次突变，每对轮齿上至少有3个交替点，交替撞击数增加为齿数的3倍以上(通常交替撞击数等于齿数)．在一个齿距角内撞击次数越多，噪声就越大越尖．

通过以上分析可知，不同交替形式引起的啮合冲击类型不同．根据齿对交替过程中有无顶刃啮合，可以把轮齿交替分为有顶刃啮合(Ⅳ、Ⅴ、Ⅵ)和无顶刃啮合(Ⅰ、Ⅱ、Ⅲ)两大类，有顶刃啮合的交替比无顶刃啮合的交替产生的啮合冲击大．另外，齿轮受载变形后，每对轮齿的交替形式可能会发生变化，表2归纳了不同齿对交替形式在各种工作条件下对齿轮噪声的影响程度．

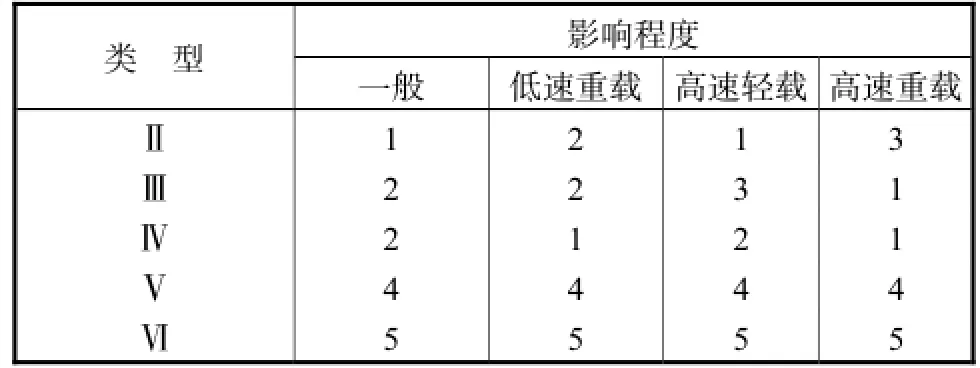
表2 各齿对交替形式对啮合冲击的影响程度Tab.2 Influence of meshing impacts under different types of teeth transition

4 啮合冲击测评系统及其实例

4.1 啮合冲击测评系统

以CZ450整体误差测量仪[15]为测量手段，利用整体误差检测结果，以前文提出的轮齿交替特性(尤其是齿对交替角)的统计量为评价指标，开发了齿轮啮合冲击测评系统(gear mesking impact evaluation system，GMIES)．

GMIES作为集测量和评价于一体的高效系统，考虑到系统应该具有良好的开放性、交互性以及与已有测量系统的集成性，系统的体系结构采用4层次的模型(见图8)，包括用户层、业务逻辑层、管理服务层和数据服务层．其中，用户层主要提供图文并茂的用户操作界面和软件系统的人机交互接口；业务处理层主要实现系统的主要功能，包括CZ450测量数据的处理、存储和搜寻，齿轮副整体误差的计算和存储，以及啮合冲击的推理、评价和解释；管理服务层为实现业务逻辑层的功能提供管理服务，主要包括用户管理、测量管理、运行管理和数据库管理；数据服务层主要实现数据和知识的集成．

在齿轮啮合冲击测评中，推理工作由推理机来完成．这里采用基于规则的推理方法(rule-based reasoning，RBR)，它是对以产生式规则表示的知识进行推理的一种方法，它通过规则的匹配而得到结论．在构建系统的规则知识库和评定知识库时，充分利用了前面介绍的轮齿交替特性与啮合冲击的关系．

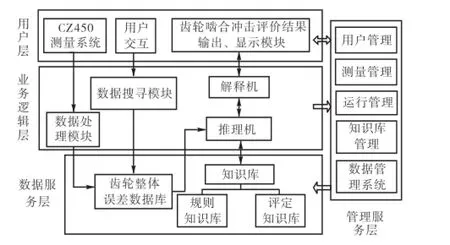
图8 GMIES的体系结构Fig.8 Architecture of GMIES

4.2 实 例

在GMIES中，对表3所示齿轮副的啮合冲击情况进行分析．图9为系统计算得到的该齿轮副的一个完整啮合周期内的齿轮副整体误差曲线．

表3 齿轮参数Tab.3 Gears’ parameters

表4 齿轮副啮合冲击情况Tab.4 Meshing impacts of gear pair

该齿轮副的一个完整啮合周期中，主动轮转5圈，从动轮转4圈，包含了100对轮齿的啮合过程．在这100对轮齿的交替过程中，一共发生了544次交替过程，引起了544次啮合冲击，具体如表4所示．

图9 齿轮副整体误差曲线Fig.9 Gear pair integrated error curve

5 结 论

(1) 齿轮传动过程中的啮合冲击情况取决于轮齿的交替特性，其中，交替部位反映了啮合冲击发生的具体位置；交替次数反映了啮合冲击产生的次数，决定了啮合冲击频率的高低；齿对交替角的统计量反映了啮合冲击的轻重程度．通过统计轮齿的交替特性可以快速评价和预报齿轮传动中引起的啮合冲击情况．

(2) 通过控制和选择不同的交替形式，可以改善齿对交替过程，从而达到减少交替过程中引起的啮合冲击、控制齿轮传动质量的效果．

(3) 通过理论与实验研究提出了一种载荷作用下齿轮啮合冲击研究的新方法：以轮齿交替特性为基础的统计学方法．

(4) 研究表明：通过齿轮副整体误差曲线来研究啮合冲击，不仅可以直观地认识啮合冲击的具体产生过程，而且可以更深入地研究啮合冲击和齿轮误差的关系；以轮齿交替特性为评价准则的啮合冲击的评价新方法可用于批量齿轮啮合冲击的评价和预报．

［1］ 盛 云，武保林. 齿轮传动中啮合冲击的计算分析[J]. 机械设计，2005，22(7)：41-43.

Sheng Yun，Wu Baolin. Calculation analysis on meshing impact in gear transmission[J]. Journal of Machine Design，2005，22(7)：41-43(in Chinese).

［2］ Dion J L，Lemoyne S，Chevallier G. Gear impacts and idle gear noise：Experimental study and non-linear dynamic model[J]. Mechanical Systems and Signal Processing，2009，23：2608-2628.

［3］ Mark W D. Analysis of the vibratory excitation of gear system：Basic Theory[J]. J Acoust Soc Am，1978，63(6)：1409-1430.

［4］ Kasuba R，Evans J W. An extended model for determining dynamic loads in spur gearing[J]. ASME Journal of Mechanical Design，1981，103(4)：398-409.

［5］ 姚文席. 修形渐开线直齿轮的啮合冲击研究[J]. 北京机械工业学院学报，2000，15(2)：2-4.

Yao Wenxi. The study of mesh impact in the transmission of modified spur gear[J]. Journal of Beijing Institute of Machinery，2000，15(2)：2-4(in Chinese).

［6］ Ganesan N，Vijayarangan S. A study of dynamic stresses in a spur gear under a moving line load and impact load conditions by a three-dimensional finite element method[J]. Journal of Sound and Vibration，1993，162(1)：158-189.

［7］ Vedmar L，Henriksson B. A general approach for deter-mining dynamic forces in spur gears[J]. ASME Journal of Mechanical Design，1998，120(6)：593-598.

［8］ Munro R G. Gear transmission error outside the normal path of contact due to corner and top contact[J]. Proc Instn Mech Engrs，1999，213(C)：389-400.

［9］ 周长江，唐进元，钟志华. 齿轮传动的线外啮合与冲击摩擦[J]. 机械工程学报，2008，44(3)：75-81.

Zhou Changjiang，Tang Jinyuan，Zhong Zhihua. Research on the corner contact and impact friction of complex gear drive system[J]. Journal of Mechanical Engineering，2008，44(3)：75-81(in Chinese).

［10］ 石照耀，康 焱. 齿轮副整体误差及其获取方法[J].天津大学学报，2012，45(2)：128-134.

Shi Zhaoyao，Kang Yan. Gear pair integrated error and its measurement method[J]. Journal of Tianjin University，2012，45(2)：128-134(in Chinese).

［11］ 黄潼年. 齿轮动态全误差曲线及其测量方法[J]. 中国科学，1974(4)：434-453.

Huang Tongnian. Gear dynamic composite error and its measurement method[J]. Science in China，1974(4)：434-453(in Chinese).

［12］ Smith J D. The uses and limitations of transmission error[J]. Gear Technology，1988，5：34-39.

［13］ 石照耀，张兆龙，谢华锟. 齿轮整体误差测量技术的发展与应用前景[J]. 工具展望，1999(2)：14-17

Shi Zhaoyao，Zhang Zhaolong，Xie Huakun. Development and prospect of the gear integrated error measuring technology[J]. Tool Review，1999(2)：14-17(in Chinese).

［14］ 石照耀，康 焱，林家春. 基于齿轮副整体误差的直齿轮动力学模型及其动态特性[J]. 机械工程学报，2010，46(17)：55-61.

Shi Zhaoyao，Kang Yan，Lin Jiachun. A comprehensive dynamics model and dynamic response analysis of a spur gear pair based on gear pair integrated error[J]. Journal of Mechanical Engineering，2010，46(17)：55-61(in Chinese).

［15］ 石照耀，唐为军. 齿轮整体误差测量系统的重构[J].机械传动，2007，31(1)：1-3.

Shi Zhaoyao，Tang Weijun. Reconstruction of the gear integrated error measuring system[J]. Journal of Mechanical Transmission，2007，31(1)：1-3(in Chinese).

Sequential Analysis and Evaluation Method of Gear Impacts

Kang Yan1,2，Shi Zhaoyao1
(1. College of Mechanical Engineering and Applied Electronics Technology，Beijing University of Technology，Beijing 100124，China；2. Institute of Manned Space System，China Academy of Space Technology，Beijing 100094，China)

On the basis of the gear pair integrated error proposed by the authors in the past，a new computing and evaluating method of gear meshing impact was introduced to effectively overcome the existing problems of present research on gear meshing impact. The emerging process of meshing impact of the gear with manufacturing errorswas explained，and three parts of teeth transition characteristic were researched. Six fundamental types of teeth transition process and their criteria were proposed. The relationship between the teeth transition types and gear meshing impact and the variation rules of teeth transition under load were introduced. Based on the above results，the gear meshing impact evaluation system(GMIES)was developed. The theoretical and simulational studies showed that the new method would be a new way to research，evaluate and control gear meshing impact.

gear；gear impact；gear noise；gear pair integrated error

TH114

A

0493-2137(2013)05-0440-08

DOI 10.11784/tdxb20130510

2011-10-09；

2012-03-25.

国家自然科学基金资助项目(50575003，50875003).

康 焱（1981— ），男，博士，kangyan416@163.com.

石照耀，shizhaoyao@bjut.edu.cn.