海上风电大直径宽浅式筒型基础抗弯特性分析

刘 润，陈广思，刘禹臣，徐 余

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 浙江财经学院教学与统计学院，杭州 310018；3. 天津市建筑设计院，天津 300074)

海上风电大直径宽浅式筒型基础抗弯特性分析

刘 润1，陈广思1，刘禹臣2，徐 余3

(1. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；2. 浙江财经学院教学与统计学院，杭州 310018；3. 天津市建筑设计院，天津 300074)

风机属于高耸结构物，承受巨大的弯矩是海上风电基础区别于其他常见结构基础的重要特征．大直径宽浅式筒型基础是适应海上风电特征荷载作用的新型基础型式．筒型基础的直径、入土深度、顶盖及侧壁厚度是控制其抗弯能力的重要技术参数．结合某海上风电工程实例，采用数值分析方法，系统研究了不同尺寸特征参数对筒型基础传递及抵抗弯矩荷载的影响，揭示了弯矩荷载作用下宽浅式筒型基础的失效模式及基础转动点位置；研究了地基承载力设计中等效均质算法的合理性．研究表明：基础抗弯承载能力随筒型基础的直径及入土深度的增加而显著增长；在弯矩荷载作用下，筒周围土体出现贯通的弧形破坏面而在基础下方土体中存在曲边三角形的稳定区；对于实际工程中的上软下硬成层土地基，经等效均质化后，将导致计算得到的基础抗弯极限承载力明显偏高．

海上风电；宽浅式筒型基础；弯矩荷载；地基承载力；破坏模式

人类进入21世纪，能源危机日益突出．海上风能作为一种可再生的清洁能源，成为缓解全球能源紧张形势的新方向．风机属于高耸结构物，承受巨大的弯矩是海上风电基础区别于其他常见结构基础的重要特征．大直径宽浅式筒型基础是海上风力发电机组的新型基础型式，正逐步应用于海上风电的基础工程中[1]．

目前对于筒型基础地基承载力的研究主要集中在揭示竖直向与水平向荷载联合作用下地基的破坏模式以及确定极限承载力方面．李向东等[2]通过模型试验来研究筒型基础在竖向、水平向荷载作用下的极限承载能力特性，并与不同承载力公式进行比较，提出了饱和软黏土筒型基础的承载力计算公式. Lian等[3]采用极限平衡及数值方法分析了筒型基础竖向、水平向及抗弯极限承载力．武科[4]围绕复合加载模式下软基上吸力式筒型基础的失稳破坏机制及其承载力特性进行了较为系统的研究．孙曦源等[5]对饱和软黏土地基中筒型基础水平承载特性进行了研究，并给出了在水平荷载作用下筒型基础转动点位置. 在筒型基础抗弯工作特性及破坏模式的研究方面，其成果则鲜见报道．

笔者结合实际工程，采用数值方法分析了筒型基础的直径D、入土深度H、顶壁厚δ及侧壁厚t对筒型基础传递及抵抗弯矩荷载的影响，分析了筒型基础在弯矩作用下的破坏模式及失稳机制，并研究了用等效均质地基法确定地基承载力与成层土地基法的差异，进而提出了对工程设计有参考价值的建议．

1 数值模拟方案

针对海上风电机组的受力特点，天津大学提出了具有较好抗弯性能的宽浅式筒型基础(见图1)．与传统的筒型基础相比，其高径比小．

图1 宽浅式筒型基础Fig.1 Wide-shallow bucket foundation

通过ABAQUS大型通用有限元软件建立筒型基础数值分析模型，如图2所示．经试算，模型尺寸径向取基础直径的6倍，竖直向取基础埋深的6倍．计算中分别改变筒型基础的直径、入土深度、壁厚进行对比分析，并以实际工程设计参数D=30,m、H= 6,m、δ=0.3,m、t=0.4,m为主要比较工况．具体的计算工况见表1．

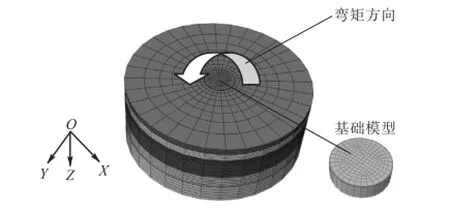
图2 有限元分析模型Fig.2 Model of FEM

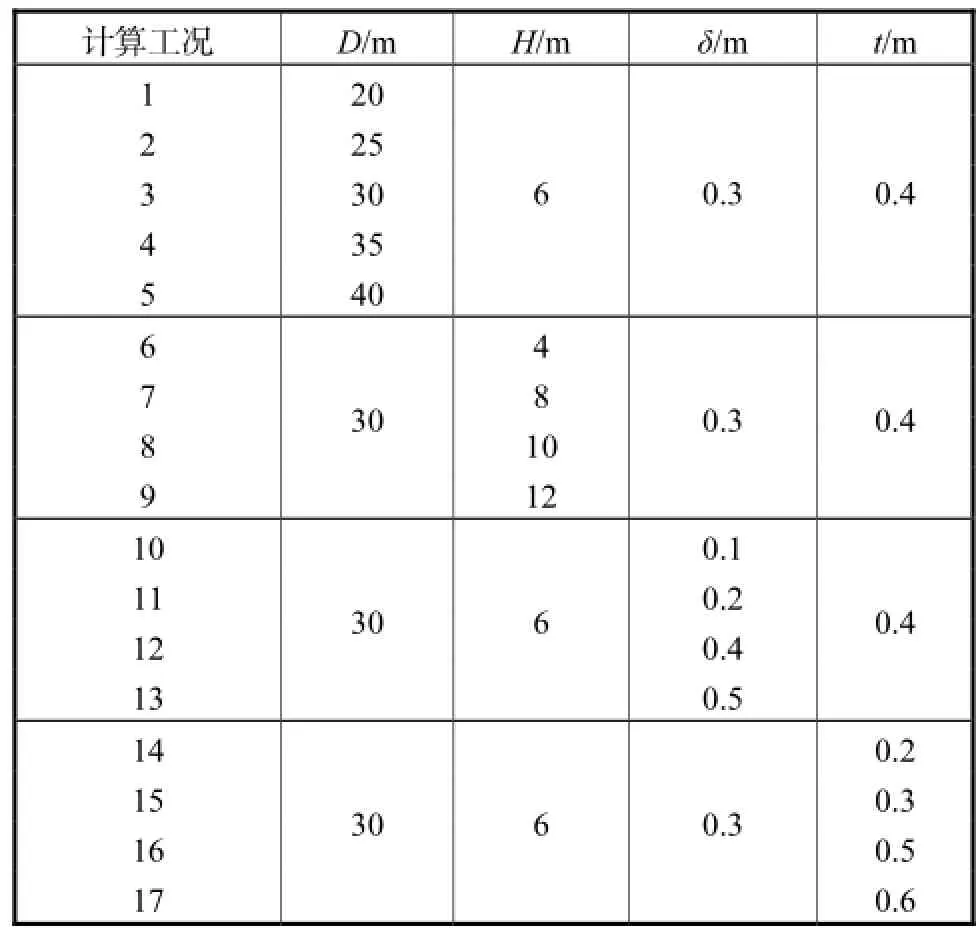
表1 筒型基础数值模拟方案Tab.1 Numerical simulation scheme of bucket foundation

研究表明，在浅基础的竖向承载力分析中，采用位移控制法较荷载控制法更为有效．为了得到荷载-位移曲线，对分析模型施加0.2,rad的转角位移，其加载方向见图2，以获得弯矩M-转角位移θ曲线．结构物与地基土之间的接触关系是有效模拟实际工况的关键，在ABAQUS的模拟中，结构物与土体的接触行为服从Coulomb摩擦定律[6]，摩擦系数的选取对计算结果有较大的影响．此次分析中筒-土摩擦系数取0.4，筒型基础模型采用弹性模型，弹性模量为3.65× 104,MPa．土体模型采用摩尔-库伦弹塑性本构模型[7]，各个土层的计算参数取自某海上风电工程的勘察数据，见表2，表中，γ′为有效重度；SE为压缩模量；φ为内摩擦角；uC为不排水抗剪强度；akf为地基承载力特征值．土体采用C3D8R单元类型进行模拟．模型侧面边界条件为约束X、Y方向位移，底面边界条件为约束X、Y、Z方向位移．

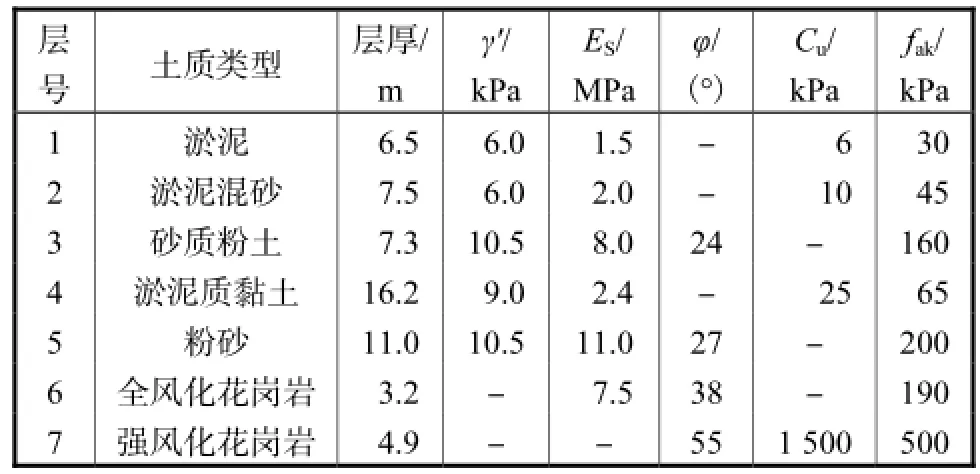
表2 地基土物理力学参数Tab.2 Physical and mechanical parameters of foundation soil

为了考察土体分层情况对地基承载力的影响，对比分析了成层土地基与规范中汉森公式提出的等效均质地基法的差异．在以上分析的基础上，按照汉森公式将成层土转化为均质土进行数值模拟，简化的土体的物理力学参数见表3，其中Zmax为持力层的最大深度；γ′为等效有效重度；φ为等效内摩擦角；Cu为等效不排水抗剪强度．

表3 等效均质土计算参数Tab.3 Calculation parameters of equivalent homogeneous soil

2 数值分析结果

2.1 筒型基础抗弯承载模式分析

图3给出了工况3中筒型基础地基土的受力变化过程，图中θ为筒型基础的转角位移．从图中可以看出，随着弯矩的增加，受压侧筒壁底部及上倾侧筒壁下部的土体出现塑性变形区；随着弯矩的继续增加，塑性区沿3个方向继续延伸，分别是沿筒型基础外侧壁向上发展，从筒型基础受压侧筒壁边缘斜上发展至基础内侧底面，同时从受压侧土体开始向斜下方向发展，发展直第3层砂质粉土后，沿土层分界面向筒内方向发展．上倾侧下部在筒型基础外侧，由于土体受筒壁向上的挤压作用，也存在明显的塑性区．最终形成受压侧土体向下运动，挤压筒内土体向上倾侧运动，与条形基础在受弯矩时的破坏模式相类似[8]，形成一个弧形的破坏面，其变化过程见图3．从图3中亦可看出，随着塑性区的发展，在筒型基础的下方存在应力状态较稳定的曲边三角形稳定区．

图3 不同θ下地基等效塑性应变及位移矢量Fig.3 Effective plastic strain and displacement vector under different θ

2.2 结构尺寸对筒型基础抗力的影响

图4～图7列出了筒型基础在不同尺寸特征参数条件下的弯矩M-转角θ位移曲线．从图中可以看出，随着各项特征参数的增加，其弯矩承载能力都增大．其中，极限弯矩随D和H的变化最为显著，而顶壁厚度与侧壁厚度的增加对弯矩极限承载力也有提高作用，但是提高效果不明显．因此，D和H是两个影响筒型基础抗弯承载力的重要特征参数．将筒型基础顶部所施加的转角达到0.05,rad时对应的弯矩荷载确定为抗弯极限承载力．

图7 不同t下的M-θ曲线Fig.7 M-θ curves with different t

表4 不同工况下抗弯极限承载力Tab.4 Ultimate bearing capacity of moment under different operating conditions

为了研究D和H的变化对筒型基础抗弯能力的影响，将同一参数变化系列中两相邻变化工况之间的抗弯极限承载力之差定义为增长量ΔM，ΔM与其中较小抗弯极限承载力的比定义为抗弯承载力增长率η．图8和图9给出了ΔM、η随D及H的变化情况．

图8 ΔM与η随D的变化Fig.8 Variation of ΔM and η with D

计算模型的不同工况下的抗弯极限承载力Mu如表4所示．

图9 ΔM与η随H的变化Fig.9 Variation of ΔM and η with H

由图8和图9可知，设计入土深度不变，在筒径增加的过程中，虽然ΔM明显增大，但增长幅度下降，说明对于给定的入土深度存在与抗弯承载力对应的最佳筒径；与此不同，当筒径不变时，随着入土深度的增加，ΔM与η增长曲线出现拐点，说明设计中对于给定的筒径存在入土深度的合理取值范围．

2.3 筒径及入土深度对地基破坏模式的影响

图10为D从20,m增加到40,m情况下地基土的等效塑性应变及位移矢量．从图中可以看出，在不同D的情况下，地基的破坏模式基本相同；但随着D的增加，其塑性区范围逐步扩大，特别是在筒型基础受压侧，由筒壁下缘到基础内侧塑性区域明显变大，从等效塑性应变图中可以看出稳定区的范围逐渐减小，从位移矢量图也可以看出D的增加使筒型基础下方土体从受压侧向上倾侧移动趋势明显，因此当筒型基础径长比变大时，筒内土体将逐步参与抵抗弯矩荷载．由此可以判断，筒型基础的抗弯能力来自下压侧的地基承载力与被动土压力，且以下压侧的地基承载力为主．

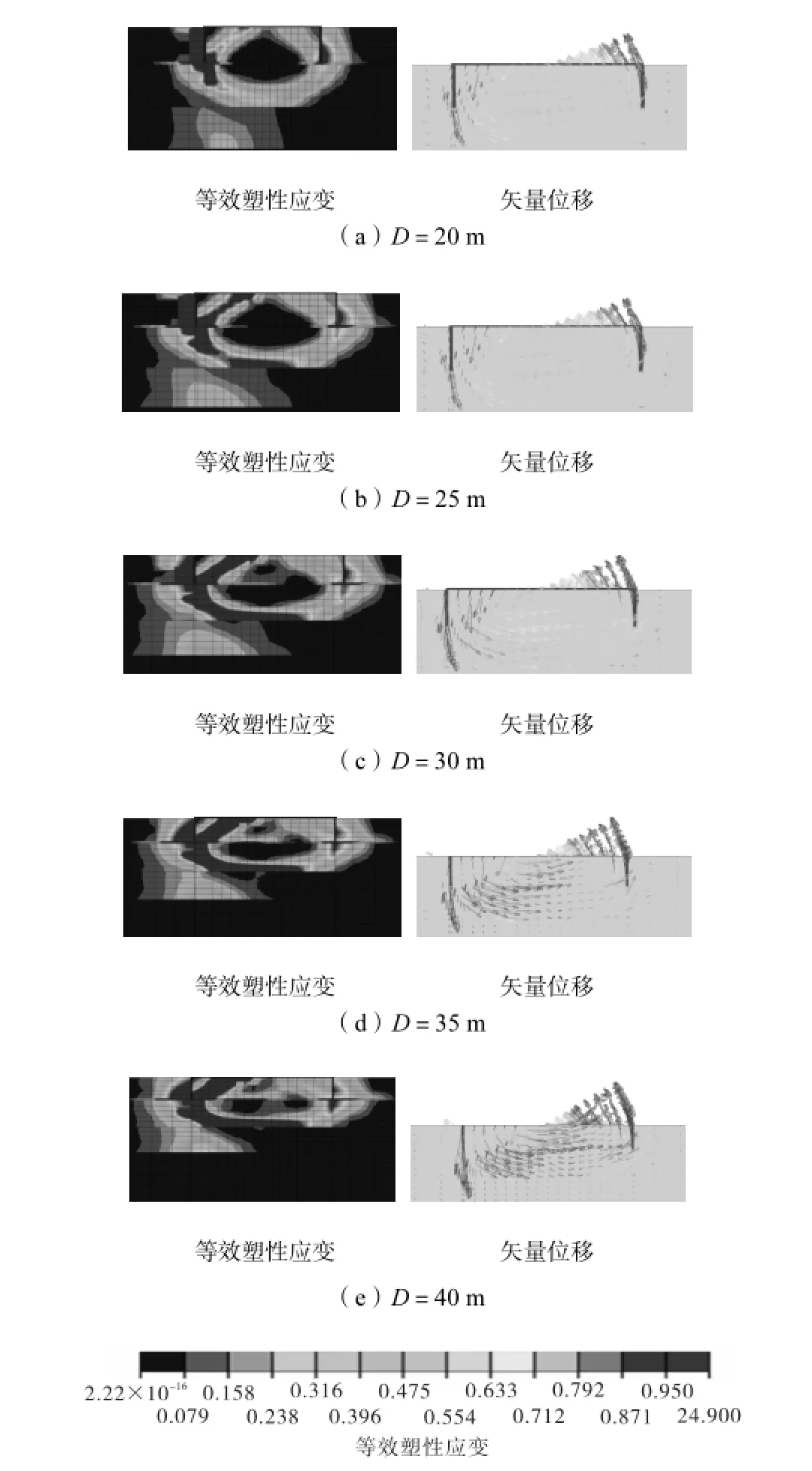
图10 不同D下的等效塑性应变及位移矢量Fig.10 Effective plastic strain and displacement vector with different D

图11为H从4,m增加到12,m情况下的筒型基础地基土的等效塑性应变及位移矢量．从图中可以看出，当入土深度改变时，地基中塑性区的发展与筒径改变的情况明显不同．随着H的增加，其塑性区的范围向深度方向不断发展扩大，且基础底部的稳定区逐渐增大．在基础的上倾侧底部，塑性区随着H的增加不断增大．从位移矢量图也可以看出，基础底部的土体随着H的增加，其向上倾侧移动的趋势明显减小．因此当筒型基础径高比变小时，基础抗弯力矩中被动土压力部分增加．

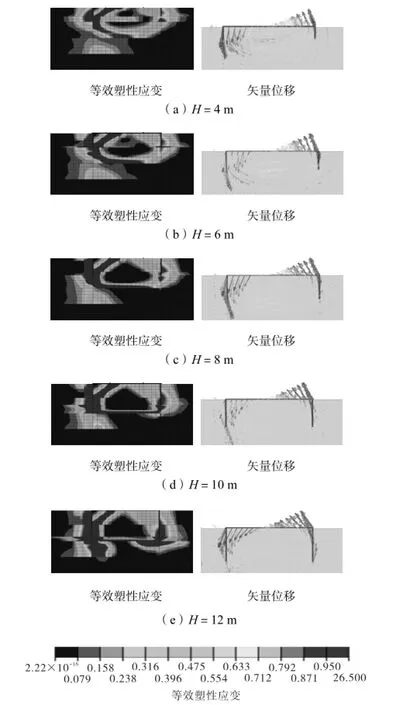
图11 不同H下的等效塑性应变及位移矢量Fig.11 Effective plastic strain and displacement vector with different H

2.4 筒型基础抗倾覆验算中转动中心的确定

在筒型基础设计过程中，需要对其进行抗倾覆验算．计算中需要事先假定基础转动点的位置，然后对其进行受力分析，最终判断基础的抗倾覆稳定性．筒型基础转动点位置的确定对工程设计十分重要．有学者认为在研究筒型基础受水平荷载时，基础的破坏模式为转动破坏模式，转动中心位于泥面与基底之间的某点上[5,9]．而从分析结果可知，D和H是影响基础承载力的重要特征参数，根据塑性区的变化过程，笔者认为筒型基础的转动点位于筒型基础受压侧附近，处于靠基础内侧塑性区边缘上，具体位置为：垂向上转动点距基础底面的距离与入土深度相等，水平向上转动点距基础中心线的距离与筒径和入土深度有关．定义转动点相对位置ε为基础转动点在水平向上距基础中心线的距离与基础半径的比，表5列出了分析模型中转动点的相对位置．

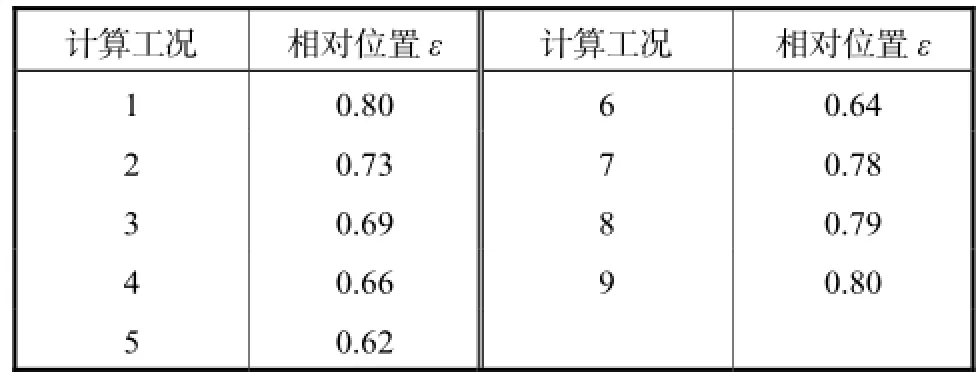
表5 转动点的位置参数Tab.5 Parameters of rotating point position

由表5可知，在H不变的条件下，相对位置ε随着D的增加而减小，即向基础中心轴移动．在D不变的条件下，相对位置ε随着H的增加而增大，即向基础边缘移动．在H/D大于0.25后，其变化基本稳定．

2.5 成层地基与等效均质地基对比分析

目前海工结构物地基承载力设计中采用等效均质土算法对成层土进行处理[10-12]．为验证这种等效算法对地基承载力的影响，对工况1～9分别建立成层土地基模型和等效均质土地基模型进行分析．图12为工况7两种地基土体等效塑性应变发展过程．

从图12中可以看出，由于成层土中第3层土为砂质粉土，与其上层土相比强度较高，在θ增大的过程中，塑性区在成层土中的发展深度比在均质土中要浅．与基础在成层土中塑性区发展相比，基础在均质土中塑性区也是从受压侧筒壁下缘开始，随着θ的增大，塑性区沿筒壁方向分别向上和向下发展．在筒壁下缘向基础底板发展的方向上，均质土体的塑性区贯通比较晚．上倾侧筒壁下缘，由筒壁向上运动产生的被动土压力比在成层土体中要小．由于均质土体是加权处理后的单一土体，与成层土体中形成一个下部接近水平的破坏面不同，其塑性区最终形成了一个圆弧形的破坏面．土体的运动趋势可以有效地反映地基的破坏模式．

图12 不同θ下成层土与均质土等效塑性应变Fig.12 Effective plastic strain of stratified soil and homogeneous soil under different θ

图13给出了不同θ下成层土与均质土位移矢量.从图中可以看出，在θ增大的同时，基础底部土体在成层土体中的运动趋势较其在均质土体中明显．对比图12可以发现，成层土体中在基础底部有效影响深度范围内存在强度较高的砂质粉土，使基础在成层土体中转动所引起的土体向下运动遇到较硬土层阻挡后，转而向基础底部发展．而均质土体中，由于没有了强度较高的粉土层，土体运动可以继续向深层发展．

筒型基础的抗弯极限载力是基础设计中的重要指标．图14反映的是在不同D的条件下，筒型基础抗弯极限承载力在成层土与均质土中的变化规律．从图中可以看出，随着D的不断增大，基础在两种土体中的抗弯极限承载力之差在不断增大．经计算，利用均质土体进行分析得出的抗弯极限承载力较成层土体平均提高40%．

图13 不同θ下成层土与均质土矢量位移Fig.13 Displacement vector of stratified soil and homogeneous soil under different θ

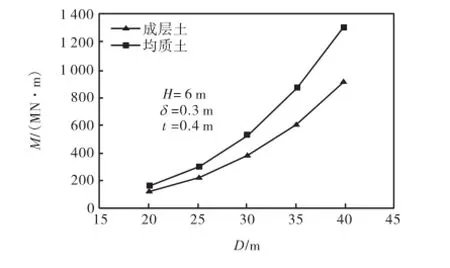
图14 不同D下成层土与均质土的抗弯极限承载力Fig.14 Ultimate bearing capacity of moment of stratified soil and homogeneous soil with different D

图15 为筒型基础在不同H条件下的抗弯极限承载力在成层土体与均质土体中的变化规律．由图可知，H的增大使得基础在两种土体中的抗弯极限承载力之差也在不断增大．经计算，利用均质土体进行分析，在改变H的条件下，得出的抗弯极限承载力较成层土体平均提高43%．

图15 不同H下成层土与均质土抗弯极限矩承载力Fig.15 Ultimate bearing capacity of moment of stratified soil and homogeneous soil with different H

3 结 论

(1) 等效塑性应变的发展过程表明，由于受压侧土体向下运动，挤压筒内土体向上倾侧运动，形成一个弧形破坏面，且在筒型基础下方土体中存在曲边三角形稳定区．

(2) 特征参数分析表明，随着各项参数的增加，基础抗弯承载能力都增大．其中，抗弯承载能力随D及H的变化最为显著，而当δ与t增加时，抗弯能力提高不明显．

(3) 在弯矩荷载作用下，当D增加时，塑性区向稳定区方向发展，使得稳定区的范围逐渐减小；D不变、H增加的情况下，塑性区向深度方向不断发展扩大，使得基础底部的稳定区逐渐增大．

(4) 地基抗倾覆验算转动点位置的研究表明，在H恒定的条件下，相对位置ε随着D的增加而减小，即向基础中心移动；在D恒定的条件下，相对位置ε随着H的增加而增大，即向基础边缘移动，并在高径比H/D大于0.25后，其变化基本稳定．

(5) 对于实际工程中的上软下硬成层土地基，经等效均质化后，地基土的塑性区发展深度比成层土深，基础底部土体的运动趋势较成层土小，导致计算得到的筒型基础抗弯极限承载力明显高于实际工程中成层土的情况．

［1］ 丁红岩，于 瑞，张浦阳. 海上风电大尺度预应力筒型基础结构预应力优化设计[J]. 天津大学学报，2012，45(6)：473-480.

Ding Hongyan，Yu Rui，Zhang Puyang. Optimal design for prestress of large-scale bucket foundation for offshore wind turbine[J]. Journal of TianjinUniversity，2012，45(6)：473-480(in Chinese).

［2］ 李向东，王建华，杨海明，等. 软土地基中单桶基础承载力的模型试验研究[J]. 勘察科学技术，2007 (3)：3-5.

Li Xiangdong，Wang Jianhua，Yang Haiming，et al. Study of model test on bearing capacity of bucket foundation in soft soil foundation[J]. Site Investigation Science and Technology，2007(3)：3-5(in Chinese).

［3］ Lian Jijian，Sun Liqiang，Zhang Jinfeng，et al. Bearing capacity and technical advantages of composite bucket foundation of offshore wind turbines[J]. Transactions of Tianjin University，2011，17(2)：132-137.

［4］ 武 科. 滩海吸力式桶形基础承载力特性研究[D]. 大连：大连理工大学建筑工程学部，2007.

Wu Ke. A Study on Bearing Capacity Behavior of Suction Bucket Foundation in Beach-Shallow Sea[D]. Dalian：Faculty of Infrastructure Engineering，Dalian University of Technology，2007(in Chinese).

［5］ 孙曦源，栾茂田，唐小微. 饱和软黏土地基中桶形基础水平承载力研究[J]. 岩土工程学报，2010，31(2)：667-672.

Sun Xiyuan，Luan Maotian，Tang Xiaowei. Study of horizontal bearing capacity of bucket foundation on saturated soft clay ground[J]. Rock and Soil Mechanics，2010，31(2)：667-672(in Chinese).

［6］ 许宏发，王 斌，戴小平，等. 桩土接触面力学参数取值研究[J]. 河海大学学报：自然科学版，2001，29(B12)：54-56.

Xu Hongfa，Wang Bin，Dai Xiaoping，et al. Determination of mechanical parameters on pile-soil interface[J]. Journal of Hohai University：Natural Sciences，2001，29 (B12)：54-56(in Chinese).

［7］ 张学言，闫澍旺. 岩土塑性力学基础[M]. 天津：天津大学出版社，2004.

Zhang Xueyan，Yan Shuwang. Fundamentals of Geotechnics Plasticity[M]. Tianjin：Tianjin University Press，2004(in Chinese).

［8］ Zhang Qiyi. Failure mode of foundation under combined loadings[J]. Electronic Journal of Geotechnical Engineering，2008，13：8-10.

［9］ Hung L C，Kim S R. Evaluation of vertical and horizontal bearing capacities of bucket foundations in clay[J]. Ocean Engineering，2012，52：75-82.

［10］ 钱家欢，殷宗泽. 土工原理与计算[M]. 北京：中国水利水电出版社，1996.

Qian Jiahuan，Yin Zhongze. Geotechnical Principles and Calculating[M]. Beijing：China Water Conservancy and Electricity Press，1996(in Chinese).

［11］ 中交天津港湾研究工程院有限公司. JTS 147—2010港口工程地基规范[S]. 北京：人民交通出版社，2010.

Tianjin Port Engineering Institute Ltd of CCCC First Harbor Engineering Company Ltd. JTS 147—2010 Code for Soil Foundations of Port Engineering[S]. Beijing：China Communications Press，2010(in Chinese).

［12］ American Petroleum Inst. Recommended Practice for Planning，Designing，and Constructing Fixed Offshore Platforms[R]. Washington，USA：American Petroleum Inst，2000.

Resisting Moment Behavior of Large Diameter and Shallow Buried Bucket Foundation for Offshore Wind Turbine

Liu Run1，Chen Guangsi1，Liu Yuchen2，Xu Yu3
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；2. School of Mathematics and Statistic，Zhejiang University of Economic and Finance，Hangzhou 310018，China；3. Tianjin Architecture Design Institute，Tianjin 300074，China)

The wind turbine belongs to high-rise structure. Thefoundation of wind turbine must bear huge moment, which is different from other common structure foundations. The large diameter and shallow buried bucket foundation is a new foundation type which meets the requirement of the characteristic load of offshore wind turbine. The important technological parameters of bucket foundation for resisting moment are diameter, embedded depth, upper wall and lateral thickness. An offshore wind power project is taken as an example, and the impacts of the characteristic parameters of different size onbucket foundation transferring and resisting moment load are systematically studied by numerical simulation. The failure mechanisms and rotating point position of bucket foundation are revealed under moment load. The rationality of equivalent homogeneous algorithm is studied in designing the bearing capacity of the foundation. Research shows that the bearing capacity of resisting moment increases significantly with the increase of diameter and embedded depth. Under the moment loads, arc failure surface occurs in the surrounding soils of bucket foundation, and the curved edge triangle stability region is found under the foundation soil. In practical engineering, the bearing capacity of resisting moment is obviously improved after the equivalent homogenizationof the stratified foundation soil which contains the soft layer on top of the hard layer.

offshore wind turbine；large diameter and shallow buried bucket foundation；moment load；bearing capacity；failure mechanism

TU443

A

0493-2137(2013)05-0393-08

DOI 10.11784/tdxb20130503

2012-11-27；

2013-01-08.

国家高技术研究发展计划(863计划)资助项目(2012AA051702)；国家自然科学基金创新研究群体科学基金资助项目(51021004)；天津市自然科学基金资助项目(12JCYBJC14700)；国家国际科技合作专项项目(2012DFA70490)．

刘 润（1974— ），女，博士，教授．

刘 润，liurun@tju.edu.cn．