Sigma-Point卡尔曼滤波用于OFDM载波频偏估计
2013-06-24张鑫明门爱东
张鑫明,叶 锋,杨 波,门爱东
(1. 北京邮电大学信息与通信工程学院,北京 100876;2. 中国舰船研究院新技术研究室,北京 100192;3. 福建师范大学数学与计算机科学学院,福州 350001)
Sigma-Point卡尔曼滤波用于OFDM载波频偏估计
张鑫明1,2,叶 锋1,3,杨 波1,门爱东1
(1. 北京邮电大学信息与通信工程学院,北京 100876;2. 中国舰船研究院新技术研究室,北京 100192;3. 福建师范大学数学与计算机科学学院,福州 350001)
对于非线性的动态状态空间模型,扩展卡尔曼滤波(EKF)通过泰勒展开拟合系统的状态和观测方程,以获得对状态值的估计,但其存在估值波动大、收敛慢等缺点;而基于Sigma-point点的卡尔曼滤波方法,则是通过确定性采样实现统计特性上的近似,从而获得更为准确的高阶统计特性.为此,建立了正交频分复用(OFDM)载波频偏的动态状态空间模型,并将Sigma-point卡尔曼滤波用于其频偏估计.仿真结果表明,该类方法可以捕捉更为准确的高阶特性,其估值准确、收敛速度快、波动小、对观测噪声大小不敏感.
Sigma-point卡尔曼滤波;动态状态空间;正交频分复用;载波频偏
基于近似一个高斯分布比近似一个任意的非线性函数容易的观点,Julier等[1]提出了无迹卡尔曼滤波(unscented Kalman filter,UKF),Ito等[2]提出了中心差分卡尔曼滤波(central difference Kalman filter,CDKF),这些算法通过一组确定性采样点(Sigma points)来捕获系统的相关统计参量,将非线性映射直接作用于各Sigma 点,根据映射后的点集重建统计参量,然后根据新的统计参量重新选择Sigma 点集并重复上述过程.这种方法可以在不必对非线性映射近似的情况下,使一个随机变量的分布按非线性映射递推传播.
这类基于Sigma采样点的的滤波方法在工业控制、航空航天、导航、跟踪等领域获得了广泛的关注与应用.文献[3]利用UKF算法设计了观测器,以估计无刷直流电机的转子位置和角速度.文献[4]采用改进的UKF方法进行数据融合,并直接计算北斗组合系统导航参数的最优估计.Sigma点卡尔曼滤波也被用于基于Wi-Fi信号的室内定位与跟踪[5].
在正交频分复用(orthogonal frequency-division multiplexing,OFDM)系统中,其载波频偏问题是一个非线性估计问题,可将其描述为动态状态空间模型(dynamic state-space mode,DSSM)进行分析[6].笔者引入并分析了Sigma-point卡尔曼滤波器性能[7],并将其用于OFDM的载波频偏估计.
1 OFDM载波频偏的DSSM模型
1.1 DSSM模型描述及其求解
不考虑外部输入控制时,DSSM模型可表示为

式中:Xk为k时刻的状态变量;Yk为其可观测量;f为状态函数;h为观测函数;w、v分别为过程噪声和观测噪声.理论上,迭代Bayesian估计方法可以获得该模型的完备解,但由于高维积分通常不易求解,Bayesian估计只对某些特定的动态状态空间模型具有解析解,大多数情况下只能寻求次优估计.特别是在高斯近似的条件下(噪声等随机变量服从高斯分布),当f、h为线性函数时,Bayesian递推对应的最优解析解即为Kalman滤波法.而对于f、h为非线性的情况,常用的一种方法是扩展卡尔曼滤波(extended Kalman filter,EKF),EKF通过泰勒展开,对f、h分别进行线性逼近,使得Kalman滤波得以应用到非线性问题中.但当非线性效应明显时,截断意味着丢失了高阶项的非线性特性,同时EKF需要计算Jacbean矩阵,导致计算量过大.
与对函数本身的拟合不同,另一种思路是对系统的概率密度分布进行拟合.采样状态的先验分布,并对采样点加以加权、筛选等再处理,最终得到近似分布,从而获得状态估值.根据采样方式的不同,可分为确定性采样滤波与随机性采样滤波,前者即为Sigma-point卡尔曼滤波而后者指粒子滤波.Sigmapoint法与粒子滤波不同之处在于,其只需少量的样点即可获取系统的统计特性,且算法性能及复杂度都适中,而粒子滤波则需要大量的采样点(即粒子).本文主要研究Sigma-point卡尔曼滤波法.
1.2 OFDM载波频偏的DSSM描述
OFDM的载波频偏问题如图1及式(3)所示,不考虑信道影响时,接收信号y(n)中既有噪声项又有频偏导致的相位差[8],即
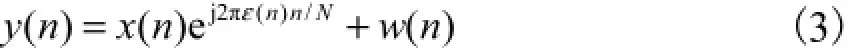
通常在一个OFDM符号内,信道是时不变或准静态的,此时的频偏因子可以视为常值,即在一个OFDM符号内有ε(n)= ε(n-1).此式与式(3)可分别视为状态方程与观测方程,则可得OFDM载波频偏问题的DSSM模型[9]为
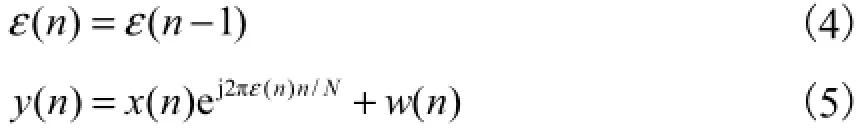
对于该模型,可以运用Sigma-point卡尔曼滤波法进行载波频偏的估计,以获得更高的估计精度和更优的收敛性.
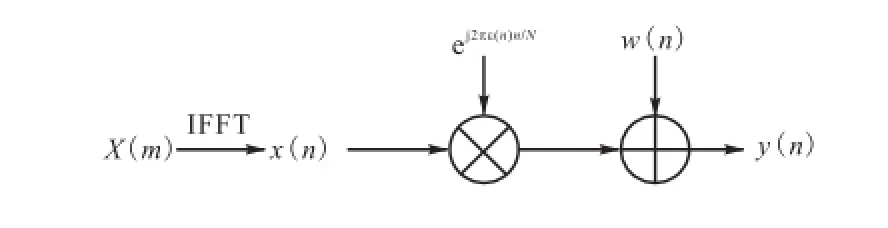
图1 OFDM频偏模型Fig.1 Carrier frequency offset of OFDM
2 Sigma-point卡尔曼滤波
Sigma-point卡尔曼滤波基于确定性采样,从待估变量的先验分布上采样n个点,对每一个点作相应的函数变换,再计算得到变换后的n个对应值的后验统计特征,如均值和方差等,进而延用卡尔曼滤波的框架结构.相较于函数拟合的方法,该方法对非线性状态和过程方程的描述更为准确.其主要包括UKF与CDKF以及为减少计算开销和提高稳定性而导出的平方根形式.
2.1 UKF
UKF通过无迹变换(unscented transformation,UT)变换实现概率分布上对非线性函数的近似.UT变换的采样Sigma点与原随机变量样点有相同的一、二阶统计特性,而其经过非线性函数传递后对应的样点,其统计特性可以准确到三阶[10].经过UT变换得到一、二阶统计特性之后,再结合卡尔曼滤波框架就得到了UKF的完整过程.
不同的采样策略对应不同的UT变换方法,有对称采样、单形采样等,最为常见的是采用尺度可变对称采样策略的标准UKF算法,其流程[11]如下所述.
1) 初始化及构造Sigma点集
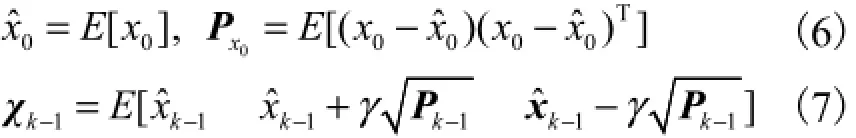
2) 状态更新
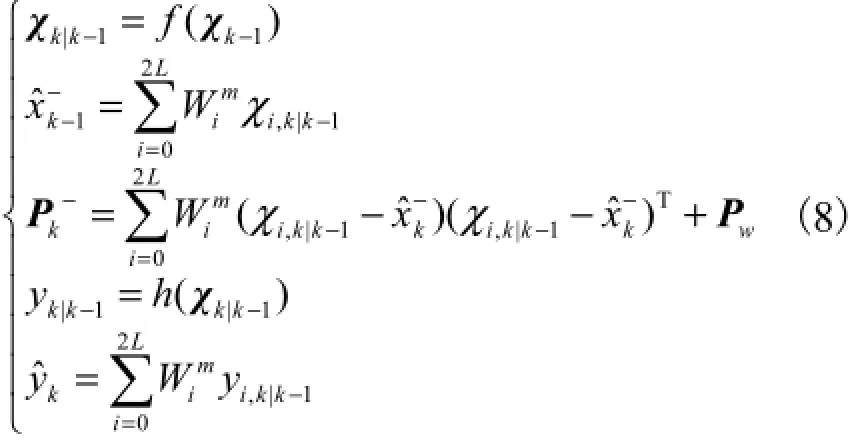
3) 观测更新
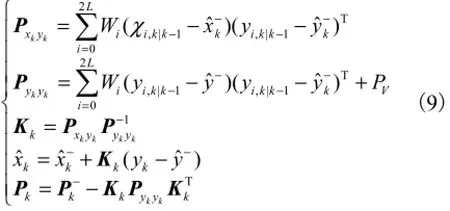
UKF滤波器的权重因子及相关参数为
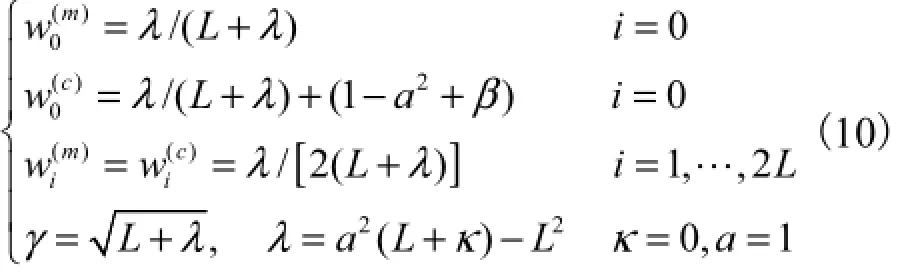
式中:γ、λ均为尺度参数;常量a描述了采样点的分布范围,通常取10-4<a<1;κ为二阶尺度参数;β用于体现变量先验分布信息,高斯分布下一般取β=2.
2.2 中心差分卡尔曼滤波
基于Stirling内插公式,利用中心差分代替EKF中泰勒展开的一、二阶级数,可以得到中心差分卡尔曼滤波 CDKF方法.
Stirling公式为
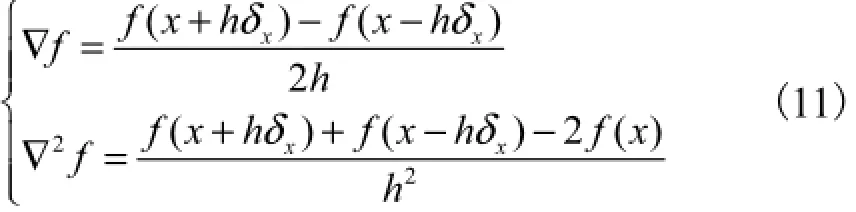
替代EKF的泰勒级数为
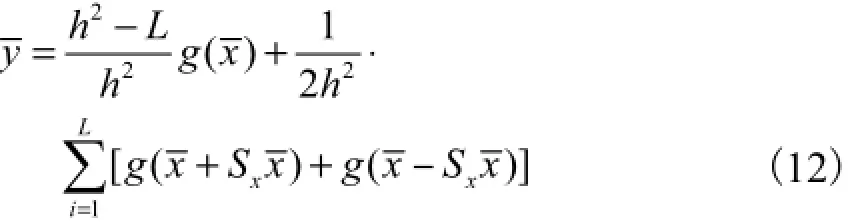
由式(12)可以看出,选取的样点x经过非线性函数变换后,对应的后验随机变量的一阶矩可以由x及分别经非线性变换后的值及对应的权重确定.实际上,其二阶矩方差及互方差[8]也是由这些采样点对应表示的,即
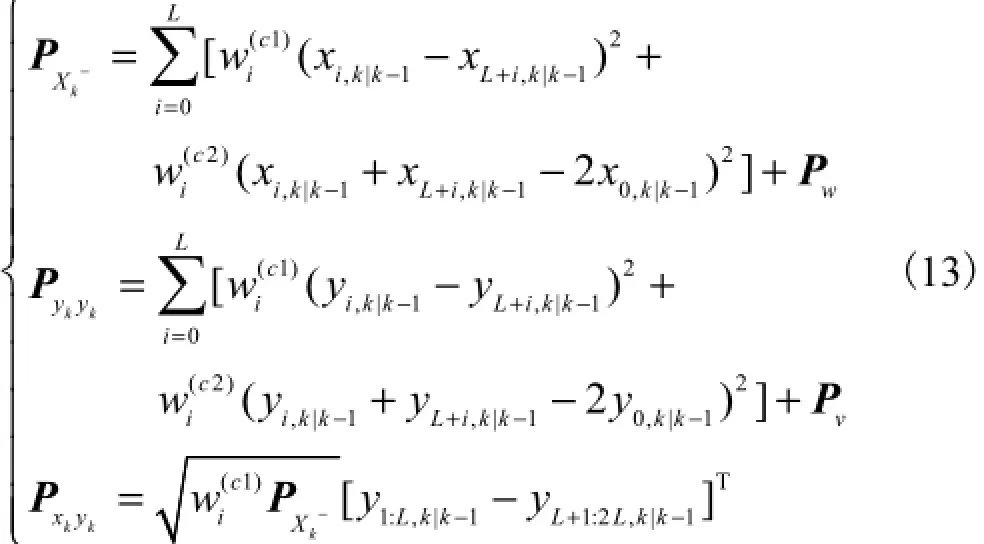
从导出的结果看,虽然Stirling公式与泰勒展开看上去相似,但CDKF滤波最终结果却与UKF相似,体现为基于确定性采样的估计.
CDKF滤波器的权重因子及相关参数为

其中:i=1,2,…,2L;h因子描述了样点的分布范围,即
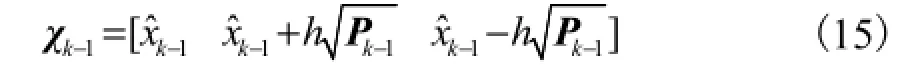
在高斯分布下,通常取23h=.
2.3 平方根形式Sigma-point卡尔曼滤波
在Sigma-point卡尔曼滤波中,为了构成Sigma点集,每次更新都要计算协方差矩阵的平方根,导致较大的计算开销.平方根形式的Sigma-point卡尔曼滤波利用矩阵QR分解、Cholesky分解因数更新以及高效最小二乘等强有力的线性代数技术,以Cholesky分解因数的形式直接传播和更新状态协方差矩阵的平方根,从而可以提高计算效率,增强数值稳定性[12].下面以UKF为例予以说明.
1)平方根形式算法流程
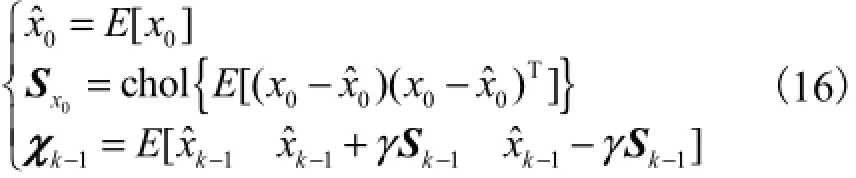
2)状态更新
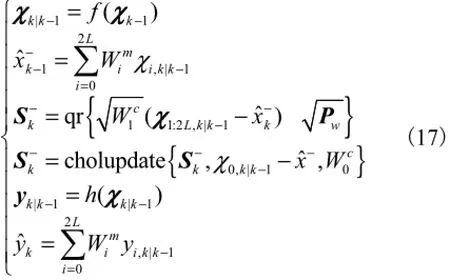
3)观测更新
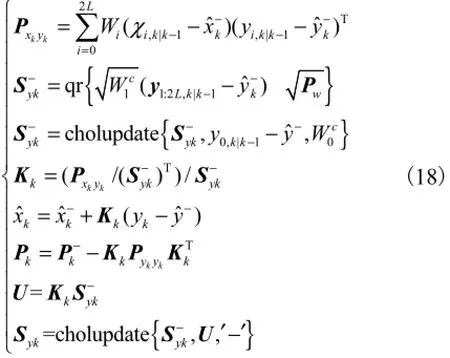
3 仿真分析
为验证Sigma-point卡尔曼滤波算法的性能,将其应用于OFDM频偏估计中.仿真条件为64子载波的OFDM系统,QPSK调制,待估计的归一化频偏因子为0.3,训练序列长度为64个星座映射符号.假设同步理想,已知信道冲击响应特性,噪声为AWGN高斯白噪.频偏因子初值设为0.01,对于UKF,滤波器参数设为κ=0,a=1,β=2;对于CDKF,参数设为h2=3.
基于Sigma-point卡尔曼滤波进行频偏估计所得的线性及Log BER曲线如图2所示.与自消除算法SC及最小方差迭代估计RLS算法相比,EKF、UKF与CDKF都获得了较为明显的BER改善.其中EKF在低信噪比条件下性能一般,而UKF与CDKF更好.滤波方法相比于RLS算法性能有较大优势是由于滤波算法以最小均方差为代价函数,充分利用了噪声统计特性,而RLS算法并没有利用噪声特性.
图3和图4分别为信噪比SNR为0、15,dB时频偏的估值曲线.可以看出UKF与CDKF算法迭代收敛过程比较稳定,估值也准确.EKF性能最差,收敛慢、波动大,特别是在低信噪比的情况下,估值偏差较大.
定义待估计变量的均方误差MSE为

式中:ix为各次迭代的估值;ˆx为真值.在信噪比分别为0,dB、5,dB、10,dB及15,dB时的均方误差值如表1所示.从表1也可以看出在估计偏差的性能上Sigma-point卡尔曼滤波优于EKF,其中UKF也是略优于CDKF.
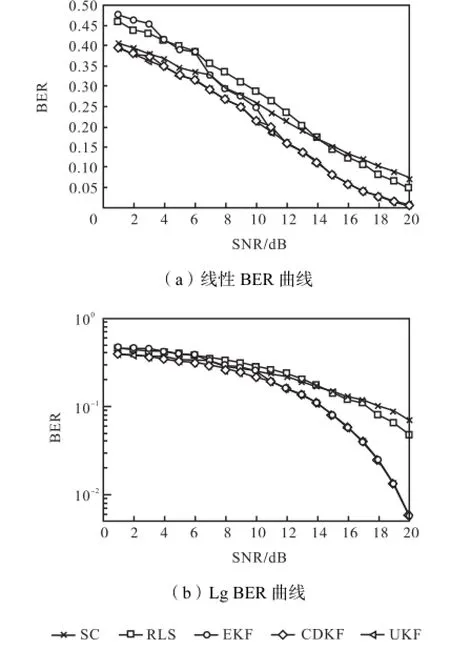
图2 不同信噪比的误码率曲线Fig.2 Error bit rate versus SNR

图3 SNR=0,dB,ε=0.3时迭代估值Fig.3 Valuation curve when SNR=0,dB,ε=0.3
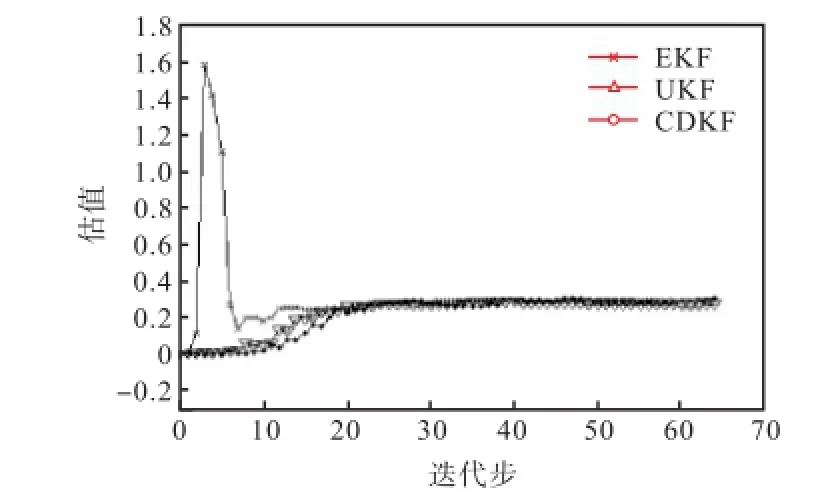
图4 SNR=15,dB,ε=0.3时迭代估值Fig.4 Valuation curve when SNR=15,dB,ε=0.3
理论上,Sigma-point卡尔曼滤波可以提升估值精度及性能,其平方根形式可以减少一定的计算量,但离实际应用还需一定的改进,可行的一种方法是考虑并行性实现.基于心动阵列的卡尔曼滤波已早有研究,但由于Sigma-point卡尔曼滤波处理非线性模型时所涉及运算更为复杂,相关的并行化研究很少.考虑到在UKF算法流程中,UT变换部分与滤波更新部分可以被视为并行的两部分结构;另一方面,通过矩阵分解,采样点集也可以分为并行的子点集进行并行处理.从而UKF等Sigma-point卡尔曼滤波的并行实现是可能的.
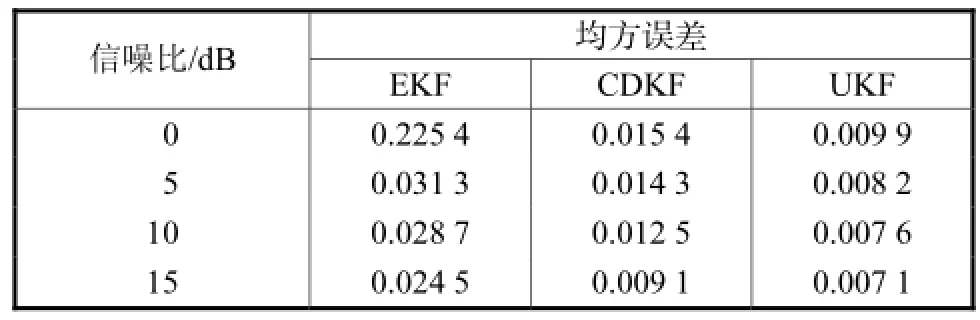
表1 估计的均方误差Tab.1 Estimated mean square error
4 结 语
对于OFDM的载波频偏估计,EKF 存在精度低、低信噪比时误差大等问题.相比EKF,Sigmapoint卡尔曼滤波估计精度高,收敛更快,估值更稳定,与信噪比关系不大,是性能较优的一种方法.并且其相对于粒子滤波而言,不需大量的随机样点,计算过程也相对简单.本文将Sigma-point卡尔曼滤波应用于OFDM频偏估计,获得了一定的性能改进.但对于Sigma-point卡尔曼滤波,由于其估计过程中需要不断更新方差等矩阵,因而实时性略差,不适于工程应用.对其及平方根形式算法的进一步优化,以及基于并行处理的应用是下一步的研究方向.
[1] Julier S J,Uhlmann J K. New extension of Kalman filter to nonlinear systems[C]// Proceedings of SPIE3068,Signal Processing,Sensor Fusion,and Target Recognition Ⅵ.Orlando,USA,1997:182-193.
[2] Ito K,Xiong K. Gaussian filters for nonlinear filtering problems[J]. IEEE Transactions on Automatic Control,2000,45(5):910-927.
[3] 史婷娜,张 倩,夏长亮,等. 基于UKF算法的无刷直流电机转子位置和速度的估计[J]. 天津大学学报,2008,41(3):338-343.
Shi Tingna,Zhang Qian,Xia Changliang. Estimates of rotor position and velocity of brushless DC motor with UKF algorithm[J]. Journal of Tianjin University,2008,41(3):338-343(in Chinese).
[4] 汪秋婷,胡修林. 基于UKF的新型北斗/SINS组合系统直接法卡尔曼滤波[J]. 系统工程与电子技术,2010,32(2):376-379.
Wang Qiuting,Hu Xiulin. Improved Kalman filtering algorithm for passive BD/SINS integrated navigation system based on UKF[J]. System Engineering and Electronics,2010,32(2):376-379(in Chinese).
[5] Paul A S,Wan E A. Wi-Fi based indoor localization and tracking using sigma-point Kalman filtering methods[C]//Position,Location and Navigation Symposium,2008 IEEE/ION. Monterey,USA,2008:646-659.
[6] Zhang Xinming,Yang Bo,Li Shan. An unscented Kalman filter for ICI cancellation in high-mobility OFDM system[C]//IEEE 73th Vehicular Technology Conference. Budapest,Hungary,2011:1-5.
[7] Van der Merwe R. Sigma-Point Kalman Filters for Probabilistic Inference in Dynamic State-Space Models[D]. Portland,USA:School of Medicine,Oregon Health and Science University,2004.
[8] Shi Qiang,Fang Yong,Wang Min. A novel ICI selfcancellation scheme for OFDM systems[C]// 5th International Conference on Wireless Communications,Networking and Mobile Computing. Beijing,China,2009:1-4.
[9] Lim Jaechan,Hong Daehyoung. Inter-carrier interference estimation in OFDM systems with unknown noise distributions[J]. IEEE Signal Processing Letters,2009,16:493-496.
[10] Julier S,Uhlmann J,Durrant-Whyte H F. A new method for the nonlinear transformation of means and covariances in filters and estimators[J]. IEEE Transactions on Automatic Control,2000,45(3):477-482.
[11] Julier S. The scaled unscented transformation[C]// Proceedings of the American Control Conference. Anchorage,USA,2002:4555-4559.
[12] Van der Merwe R,Wan E A. The square-root unscented kalman filter for state and parameter-estimation[C]// IEEE International Conference on Acoustic,Speech,and Signal Processing. Salt Lake City,USA,2001:3461-3464.
Application of Sigma-Point Kalman Filter to Carrier Frequency Offset Estimation of OFDM Systems
Zhang Xinming1,2,Ye Feng1,3,Yang Bo1,Men Aidong1
(1. School of Information and Communication Engineering,Beijing University of Posts and Telecommunications,Beijing 100876,China;2. New Technology Research Department,China Ship Research and Development Academy,Beijing 100192,China;3. School of Mathematics and Computer Science,Fujian Normal University,Fuzhou 350001,China)
For the non-linear dynamic state-space model, extended Kalman filter (EKF) fits the system state and observation equations to obtain the estimation of state, but it has deficiencies like apparent fluctuation and slow convergence. While the Sigma-point Kalman filters obtain the statistical characteristics based on deterministic samples, and accordingly better approximation can be achieved. In this paper, the orthogonal frequency-division multiplexing(OFDM) carrier frequency offset is described as non-linear dynamic state-space model(DSSM), and the Sigmapoint Kalman filter is applied to the estimation of the offset value. Simulation results show that the proposed filter perform better at capturing high order moments than EKF, with higher accuracy, faster convergence, smaller fluctuations and lower noise sensitivity.
Sigma-point Kalman filter;dynamic state-space model;orthogonal frequency-division multiplexing;carrier frequency offset
TN911.22
A
0493-2137(2013)05-0458-05
DOI 10.11784/tdxb20130513
2011-10-08;
2012-03-22.
国家自然科学基金资助项目(61072080).
张鑫明(1986— ),男,博士,工程师,bupt.zhangxinming@gmail.com.
门爱东,menad@bupt.edu.cn.
