基于PSO的支持向量机多元控制图均值偏移诊断模型

赵永满，何 桢，何曙光，张 敏

(1. 天津大学管理与经济学部，天津 300072；2. 石河子大学机电学院，石河子 832000)

基于PSO的支持向量机多元控制图均值偏移诊断模型

赵永满1,2，何 桢1，何曙光1，张 敏1

(1. 天津大学管理与经济学部，天津 300072；2. 石河子大学机电学院，石河子 832000)

为了诊断多元控制图发出的报警信号是由哪一个或者哪些变量组合发生均值偏移引起的，提出了基于粒子群优化(PSO)算法的支持向量机(SVM)多元控制图均值偏移诊断模型．模型中使用2T控制图对多元过程进行控制，在假设过程方差-协方差矩阵保持不变的前提下，根据不同的均值偏移模式，产生SVM训练数据集和测试数据集，用PSO对SVM的参数进行优化，最终得到优化的SVM模型．结果表明，基于粒子群优化算法的支持向量机模型(SVM-PSO)比基于SVM和基于神经网络(ANN)模型的分类能力更强，分类准确率超过85%．

多元控制图；均值偏移诊断；粒子群优化算法；支持向量机

随着产品和制造过程复杂性的增加，具有多个相关关键质量特性(critical to quality，CTQ)的产品制造过程越来越普遍[1]．Hotelling[2]于1947年最早提出多元统计过程控制(multivariate statistical process control，MSPC)技术．由于多个质量特性之间存在相关关系，多元控制图同时监测多个质量特性，控制图发出的报警信号只能说明过程异常，而不能解释控制图发出的报警信号是由哪一个或者哪些变量组合发生偏移引起的，在这种情况下，用多个单变量控制图分别监控生产过程各个质量特性的方法往往导致错误的结论．因此如何寻找并解释导致多元控制图报警的变量/变量组合就成为MSPC应用中一个至关重要的问题．

为了解释多元控制图的报警信号，诸多学者做了相关研究．其中，神经网络是最早应用于MSPC诊断的机器学习方法．Wang等[3]提出利用人工神经网络(artificial neural network，ANN)和模糊数学的方法建立模糊神经网络模型检测多元过程均值偏移，同时划分均值偏移量的大小，以一个二元过程的例子说明模型的具体应用过程，仿真结果显示了建立模型的有效性．Hou等[4]则利用BP神经网络监测制造过程，并划分被加工产品的质量类故障，而用粗糙集(rough set，RS)提取产品质量测量值与制造过程参数之间的因果关系，建立了ANN和RS集成的多元制造过程的智能远程监测和诊断模型．Niaki等[1]提出基于神经网络模型诊断过程变异，识别发生变异的变量及变异的方向，给出了均值偏移诊断的分类结果．Guh[5]建立了多元均值偏移识别的ANN模型，应用分类方法识别多元过程中各变量是否发生偏移、偏移方向以及偏移量．Yu等[6-7]针对多元过程监控与诊断模型特征，应用ANN和遗传算法(generic algorithm，GA)解决该问题．这类方法是用多元2T控制图识别过程异常，采用ANN来建立拟合过程质量特性及其相关统计量和变量偏移类别的分类模型，而随着质量特性维度的增加，分类的难度显著增加．

Cheng等[8]提出了基于ANN和支持向量机(support vector machine，SVM)分类器识别多元过程协方差的方法，相比之下，SVM的一个很明显的优点是比ANN更容易建立．Shao等[9]提出独立成分分析和SVM混合的方法确定导致过程突变的质量特性变量，该方法采用网格搜索技术选择SVM的参数，模型能够有效地提高对异常质量特性的正确识别率.

笔者所在课题组分析了基于支持向量机的多元统计过程控制诊断模型，以确定导致控制图报警的变量/变量组合，模型模拟过程中支持向量机的参数只选取了部分离散值，最终给出模型模拟的分类结果．Venkatasubramanian等[10]在2003年对有关MSPC诊断方面的研究成果进行了综述．

然而支持向量机模型建立时参数的选择对其泛化能力及分类准确率有较大的影响．笔者就目前支持向量机参数选择问题，提出采用基于粒子群优化(particle swarm optimization，PSO)算法对支持向量机参数进行优化选取，构建支持向量机模型分类优化模型．PSO算法相对于其他优化算法的优点是相对简单，需要调整的参数相对较少，是能够在较大程度上获得模型优化参数的随机优化技术．笔者以多元控制图为研究对象，对多元过程控制图均值偏移报警信号进行诊断，以确定导致控制图异常的变量/变量组合，模拟结果表明，基于PSO算法的支持向量机模型有更好的分类准确率．

1 多元过程控制图

多元控制图主要有3种类型：一是类Shewhart多元控制图，最典型的为T2控制图；其余两种是多元指数加权移动平均(multivariate exponentially weighted moving average，MEWMA)控制图和多元累积和(multivariate cumulative sum，MCUSUM)控制图．另外还有一系列专门应用于多元过程的控制图，详情可参考文献[11]．

假设某多元过程有p个关键质量特性，可表示为X=(X1X2… Xp)，设每个样本的样本容量为n，共有m样本．进一步假设X服从多元正态分布，即X～Np(μ0，∑0)，其中µ0和∑0分别为总体均值和方差-协方差矩阵．则T2统计量定义为

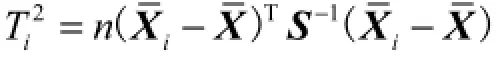
上控制限

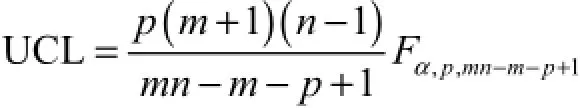
下控制限

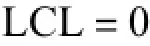
与一元控制图不同，多元控制图不但需要设计合理的统计量和控制限，而且在控制图报警后需进一步识别导致控制图报警的变量/变量组合，即多元过程控制图的异常诊断．以多元过程控制图报警信号对应的质量特性数据及相应的特征值为输入样本，应用支持向量机方法对报警信号进行分类处理，从而实现对多元控制图异常的诊断是本文的研究所在．

2 支持向量机和粒子群优化算法

2.1 支持向量机算法

SVM由Cortes和Vapnik于1995年首先提出，它在解决小样本、非线性及高维模式识别中表现出许多特有的优势，并能够推广应用到函数拟合等其他机器学习问题中[12-13]．它的目标是在结构风险最小化的基础上使得广义误差的上界最小化．有关支持向量机详细的内容可参考文献[14]．

设训练样本集D为(x1,y1)，(x2,y2)，…，(xi,yi)，其中i=1，2，…，N，N为训练样本数，xi∈Rp为p维输入向量，yi∈{+1,-1}为输出分类标识．支持向量机的训练涉及到式(1)所示二元优化问题的解决方案，即

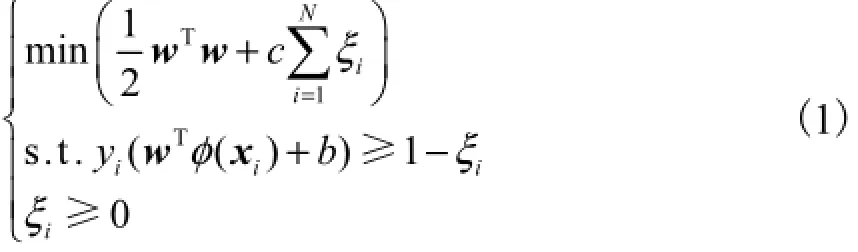
式中：c为惩罚参数；w为超平面系数向量；b为偏差项；ξi为非可分离数据处理的误差参数．惩罚参数c决定了设计误差的惩罚程度，用于控制最大间隔和分类错误之间的平衡．

在特征空间中构建分离超平面导致在输入空间非线性的决策边界，引入满足条件的核函数可以减少在高维空间有关的计算量，核函数能够直接完成在输入空间必要的计算．不同的核函数形式对应不同的算法，常用的核函数有线性核函数、多项式核函数、高斯径向基核函数和2层感知器核函数等．许多实际的问题往往都有2个以上的类别，构建多级支持向量机仍然是一个正在进行的研究课题，更多细节的内容可参考文献[15]．

在构建用于多元控制图均值诊断的支持向量机模型时，方法中的训练样本是应用多元控制图而获得．采用粒子群优化算法优选支持向量机的参数，目的是使模型的分类正确率达到最佳．

2.2 粒子群优化算法

PSO算法是由Eberhart等[16]提出的一种随机优化技术．在t时刻，设Xi(t)=(xi1(t) xi2(t) …xiN(t))为群体中微粒i的当前位置，Vi(t)=(vi1(t) vi2(t) … viN(t))为群体中微粒i的当前飞行速度，在搜索空间中m个粒子的位置可设定为X=(X1…Xj… X2… Xm)，Pi(t)=(pi1pi2… piN)为群体中微粒i所经历的最好位置，群体中所有粒子经历过的最好位置为g()tP，即全局最好位置．则在每次迭代中，粒子可根据式(2)和式(3)更新速度和位置[16]，即

式中：n为维度(1≤n≤N)；c1和c2为正的常数；r1和r2为[0,1]之间的2个随机函数；ωi为惯性权重．

惯性权重是一个随着时间线性递减的函数，惯性权重的函数形式为

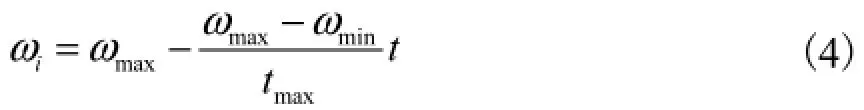
式中：ωmax为初始权重；ωmin为最终权重；maxt为最大迭代次数；t为当前迭代次数．

粒子群优化算法已在众多领域得到了广泛应用，它相对于其他优化算法的优点是相对简单，需要调整的参数相对较少，在本文中用于对支持向量机参数的优化选取．

3 基于PSO的SVM分类模型

3.1 支持向量机模型选择

构建支持向量机模型时最大的问题是如何选择核函数及相关的参数值．在目前研究中，由于高斯径向基核函数更趋于能够达到较好的性能，因此选择该核函数作为模型中的核函数．此时惩罚参数c和核函数参数g是SVM需要确定的2个参数．核参数定义了高维特征空间的具体结构，在该空间中，能够找到具有最大间隔的超平面．PSO算法本身就是一种被广泛应用的随机搜索优化算法，该算法作为一种新的优化算法，由于其具有容易理解、易于实现，并能以最大概率求得全局最优解的特点，因此本文通过模拟实验使用PSO算法对SVM模型参数进行优化选择，以便使SVM模型达到最佳的分类效果．

3.2 训练数据集的产生

应用Monte Carlo模拟方法产生大量的伪随机训练数据．假设产生伪随机数的p维多元过程满足下述条件：过程受控时，过程质量特性数据x服从参数为µ和Σ的多元正态分布，记为，其中µ为均值向量，Σ为方差-协方差矩阵，且方差-协方差矩阵Σ已知．为了问题的简化，所有的变量都进行归一化处理，过程受控时µ=0，方差σ都为1．通过这样的处理，协方差矩阵Σ与系数矩阵R的形式完全一样，也就是协方差矩阵主对角线元素都是1，其余的部分是过程变量之间成对的相关系数ρ．利用传统的多元控制图来生成均值偏移的数据，每一个得到的输入向量都必须超出2T控制图的上控制限UCL．假设在某一时刻t过程均值发生了偏移，则该时刻t后的质量数据服从参数为和的多元正态分布，其中，均值偏移量Δµ定义为为过程均值偏移系数．

考虑到输入向量对分类器性能的影响，本文采用两种不同的输入向量来进行研究，第1个输入特征向量仅由样本数据构成，第2个输入特征向量由样本数据和相应的2T值构成．对于某个具有3个质量特性的多元过程，将质量特性数据通过标准化变换表示为，则转化后的数据服从参数为μ=0和相关系数矩阵R的多元正态分布，此时输入特征向量分别是，其中T2=．令均值偏移系数分别为，则共有342种偏移模式，对于每一种偏移模式，分别产生500个数据训练样本和测试样本，同时生成1,000个过程受控状态下的数据训练和测试样本，测试样本用于估计支持向量机的性能．

3.3 基于PSO的SVM分类模型

为了优化支持向量机的惩罚参数c和高斯径向基核函数参数g，本文中构建的基于粒子群优化算法的参数选取流程如图1所示．

选择的高斯径向基核函数使粒子在编码时由惩罚参数c和核函数参数g两部分构成．支持向量机分类准确率用于估计粒子质量的适应度函数(fitness function)，函数形式为

式中：tC为正确分类的个数；fC为错误分类的个数．

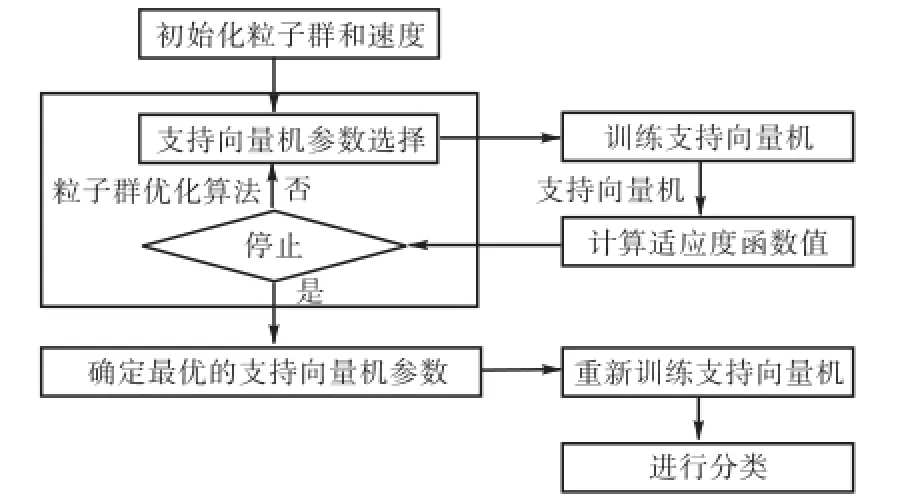
图1 基于粒子群优化算法的参数选择流程Fig.1 Parameter selection process based on PSO algorithm

4 模型模拟分析

4.1 模型参数优化

在参数优化过程中，使用基于高斯径向基核函数非线性支持向量机，给定了相应的惩罚参数c和核函数参数g的变化范围分别为[0.1，100]和[0.01，1,000]，粒子群系数值分别为种群最大数量20、加速常数为3、最大速度为8、参数局部搜索能力1c=1.5、参数全局搜索能力2c=1.7和最大的进化代数200[17].

利用生成的数据测试样本，根据图1所示的流程，模型准确度作为适应度函数值，将模型的惩罚参数c和核函数参数g作为需优化的参数，对用于多元控制图均值偏移诊断的支持向量机模型进行了优化.

(1) 输入值为特征向量(x1,x2,x3)．当模型输入只是原始数据时，通过优化得到粒子群进化代数与最佳函数数值关系曲线和变量的最佳个体值如图2(a)所示．从图可见，在粒子群进化到200代后适应度函数数值几乎不再发生变化，即认为达到其最优解，此时的最佳个体值分别为惩罚参数c=63.884,7，核函数参数g=1.159,9，分类正确率为74.171,4%．

(2) 输入值为特征向量(x1,x2,x3,T2)．通过优化得到粒子群进化代数与最佳函数数值关系曲线和变量的最佳个体值如图2(b)所示．在进化到200代后适应度函数值不再发生变化，即达到了最优解，此时的最佳个体值分别为惩罚参数c=93.757,8，核函数参数g=0.798,08，分类正确率为74.214,3%．

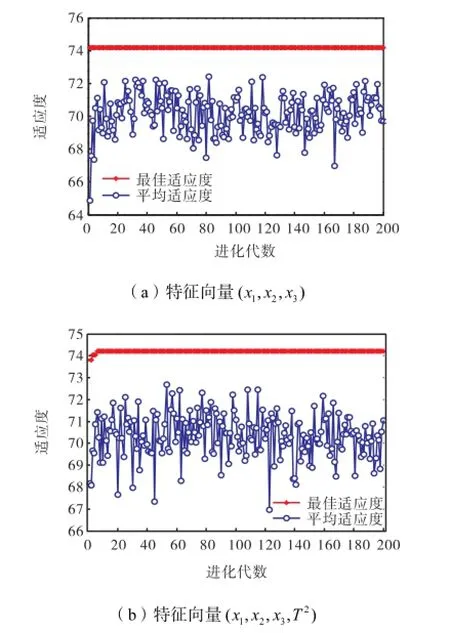
图2 PSO寻找最佳参数的适应度曲线Fig.2 Fitness curve for PSO to find the best parameters

利用得到的在粒子群优化算法下的最佳参数，可以对SVM进行进一步的训练，进而对多元过程异常模式进行分类诊断．需要说明的是，仿真研究表明，SVM-PSO模型分类正确率会依赖于输入模型的特征向量的不同而存在差异，训练特征向量的不同会对支持向量机的最终优化结果产生一定的影响，进而影响到分类正确率．

4.2 模型的性能比较

为验证模型的有效性，将本文中构建的基于PSO的SVM模型与Niaki等[1]基于ANN的方法、基于SVM的方法以及笔者前期的基于交叉验证的SVM (SVM-PO)方法进行了比较，过程参数来自文献[1]，均值向量和协方差矩阵分别为

在Niaki等[1]的研究中，就三维过程均值偏移2σ、3σ和4σ的情况进行了分类准确率测试分析，基于此，亦将过程偏移设置为2σ、3σ和4σ，对不同模型分类准确率性能进行比较研究．对于每一种给定的均值偏移模式，产生100个超出T2控制图控制限的随机变量．笔者提出的基于SVM-PSO方法与基于SVM、基于ANN及基于交叉验证的SVM方法的比较结果如表1所示，其中SVM-PSO-1表示SVMPSO模型输入特征向量是(x1,x2,x3)，而SVM-PSO-2表示SVM-PSO模型输入特征向量是(x1,x2,x3,T2)．

从表1结果可以看出，对于同样的偏移模式，几种方法的分类正确率有明显的差异，这是因为应用基于神经网络方法对质量特性变量进行分类识别时，神经网络有多个需要控制的参数，如隐含层的个数、隐含节点的个数和学习率等需要凭借经验确定，并且神经网络往往会陷入局部最优解，同时随着被研究问题维度的增加，网络分类的难度有显著增加；对基于支持向量机模型诊断多元控制图而言，支持向量机参数能在某种意义下得到最佳的参数；而在SVM-PSO模型的方法中，利用粒子群优化算法具有较好全局搜索功能的特点确定了最优的模型参数，对于测试集合的预测得到较理想的正确分类率，分类能力更强．

表1列出了几种方法分类准确率的结果，从模拟结果来看，几种方法对偏移模式的分类准确率的平均值分别为82.67%、85.81%、77.52%、75.76%和47.52%，其中SVM-PSO的分类准确率为最佳，而ANN方法的准确率最小．这一结果显示出了SVMPSO方法具有较强的三元过程均值偏移的监控与诊断能力．粒子群优化算法对支持向量机参数选取是可行的，可以在某种意义上搜索到参数的最优解．同时SVM-PSO-2方法准确率的平均值优于SVM-PSO-1方法的结果，可认为在本次实验中模型输入特征向量为(x1,x2,x3,T2)时所得模型的性能优于模型输入特征向量为(x1,x2,x3)时模型的性能．

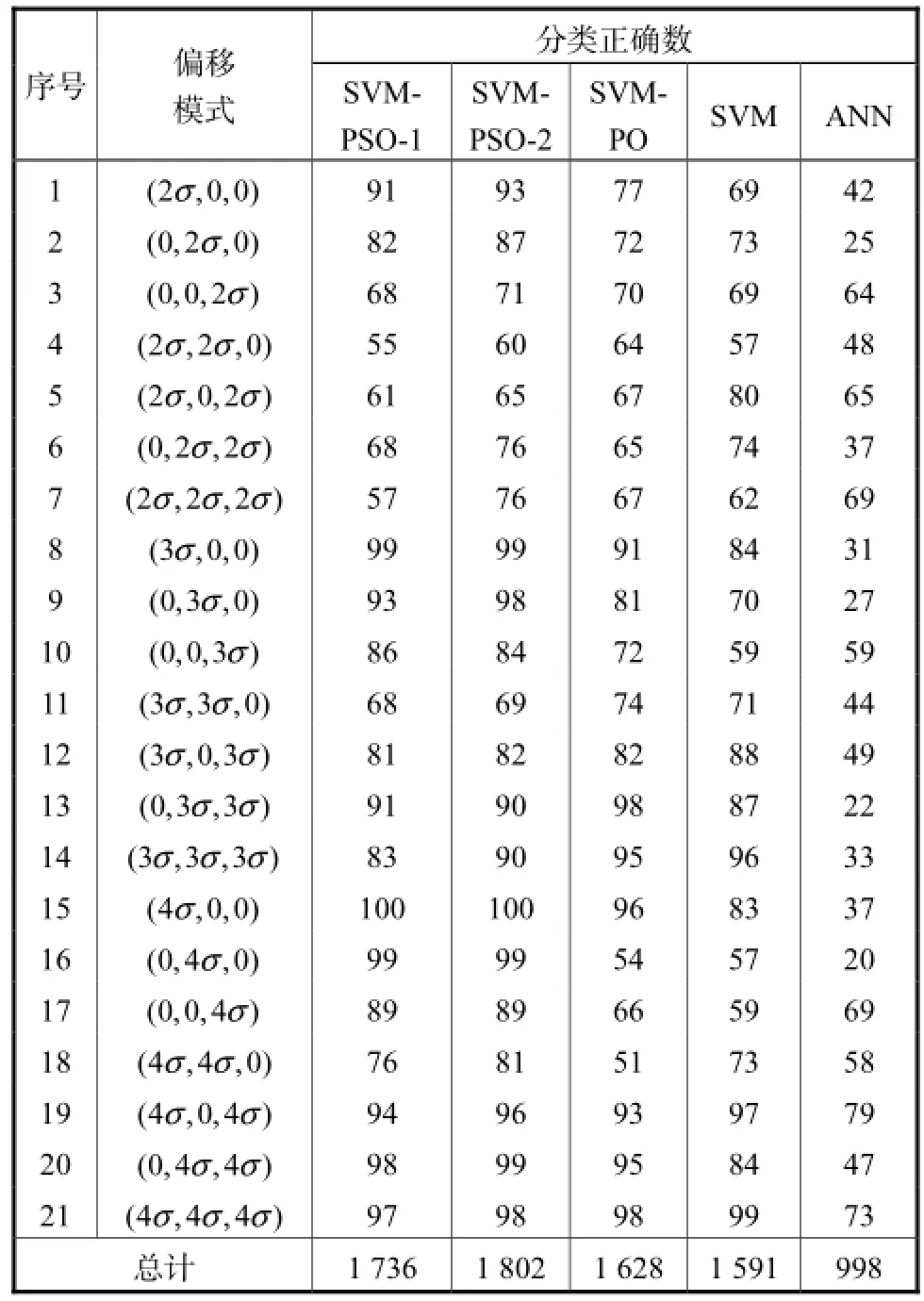
表1 基于SVM-PSO方法与基于SVM、基于ANN及基于交叉验证SVM方法的比较Tab.1 Comparison among SVM-PSO-based，SVM-based，ANN-based and SVM-cross-validation methods

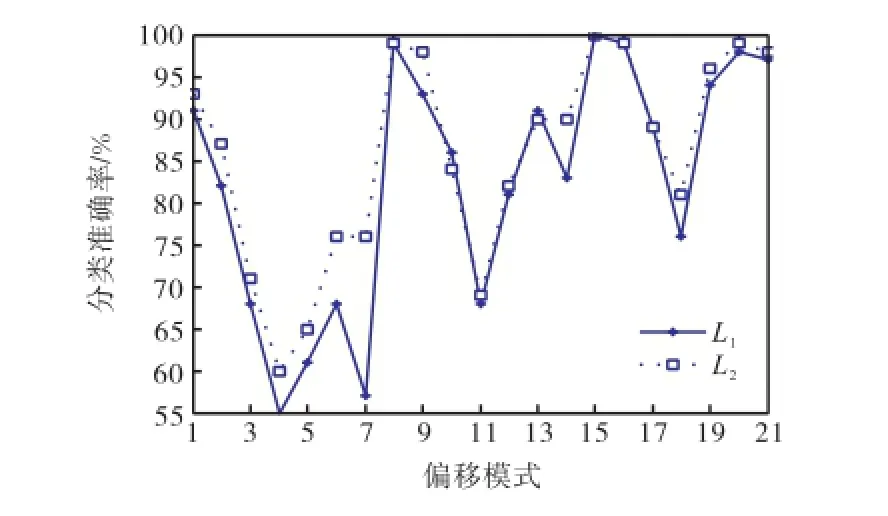
图3 不同偏移模式下SVM-PSO-1和SVM-PSO-2模型分类准确率Fig.3 Classification accuracy rate of SVM-PSO-1 and SVM-PSO-2,models in different offset modes

图3显示了不同偏移模式下SVM-PSO-1和SVM-PSO-2模型方法分类准确率曲线L1和L2，图形表明SVM-PSO-2模型的分类准确率优于SVM-PSO-1模型的分类准确率，并且除了偏移模式(2σ,2σ,2σ)和(3σ,3σ,3σ)对应的点之外，曲线点的准确率都是同时增大或者同时减小；以过程均值偏移2σ来说，对SVM-PSO-2模型对应的分类准确率曲线，分类准确率从偏移模式(2σ,0,0)的准确率93%逐渐下降到模式(2σ,2σ,0)的60%，然后又增加到偏移模式(2σ, 2σ,2σ)的76%；对于均值偏移3σ和4σ的情况分类，准确率有同样的变化规律，即都是从(kσ,0,0)准确率逐渐下降至(kσ,kσ,0)准确率，然后又增加到(kσ,kσ,kσ)准确率(其中k=3,4)．图3中还显示，3种偏移情况下，分类准确率最大的是(kσ,0,0)，最小的是(kσ,kσ,0)(其中k=2,3,4)．由图3可以看出随着均值偏移量的增加，2种模型方法对偏移模式的分类准确率有逐渐增大的趋势．

图4显示了不同偏移模式对不同模型方法分类准确率的影响，其中L1、L2、L3、L4和L5分别表示了SVM-PSO-1、SVM-PSO-2、SVM-PO、SVM和ANN模型方法的分类准确率曲线．图4表明，虽然模型SVM-PSO-1和SVM-PSO-2的整体性能更强，但是在部分偏移模式下，如偏移模式(2σ,2σ,0)、（2σ,0,2σ）和(3σ,3σ,3σ)等，模型SVM-PSO-1和SVM-PSO-2的分类准确率并未表现出其优越性，显示出该模型在分类方面的局部不稳健性，需要进一步进行研究．

图5为均值偏移量相同时不同模型的平均分类准确率曲线，M1、M2和M3分别表示均值偏移2σ、3σ和4σ时的曲线．模型SVM-PSO-1和SVM-PSO-2的分类准确率曲线表明，均值偏移量由2σ增大到4σ的同时，模型分类准确率也在同步增大，且模型SVM-PSO-2 平均分类准确率大于模型SVM-PSO-1平均分类准确率；而模型SVM-PO、SVM和ANN则不然．这一结果也表明了SVM-PSO方法的优越性．

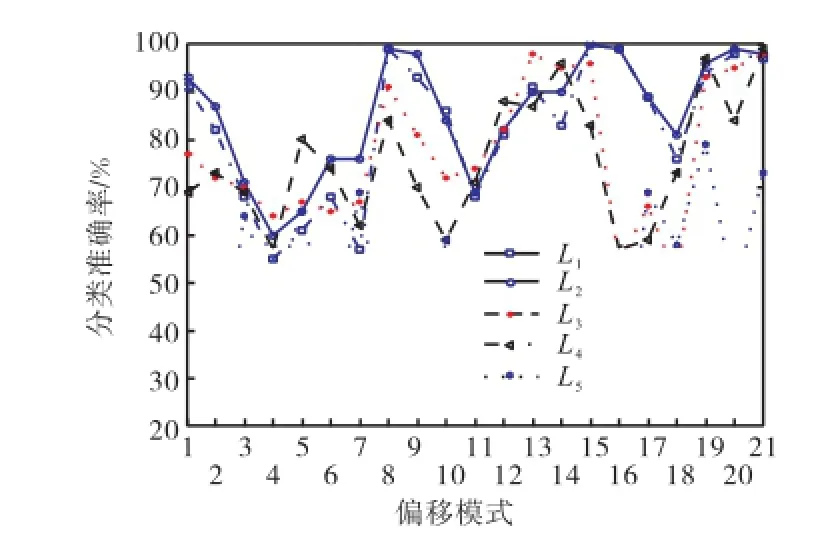
图4 在不同偏移模式下模型分类准确率比较Fig.4 Classification accuracy rate comparison of the models in different offset modes

图5 相同均值偏移量下不同模型的平均分类准确率Fig.5 Average classification accuracy of different models under the same mean offset

5 结 语

多元过程中由于多个质量特性之间存在相关关系，多元控制图同时监测多个质量特性，控制图发出的报警信号只能说明过程异常，而不能解释控制图发出的报警信号是由哪一个或者哪些变量组合发生偏移引起的．本文中提出了一种基于PSO算法的SVM多元控制图均值偏移诊断模型对多元过程进行监控与诊断，该模型能够指出过程异常的均值偏移模式．研究表明该方法与基于SVM、基于ANN及基于交叉验证SVM方法诊断多元过程的结果相比，有更好的诊断效果，且不同的输入特征向量会对构建模型的分类准确率有一定影响．

［1］ Niaki S，Abbasi B. Fault diagnosis in multivariate control charts using artificial neural networks[J]. Qual Reliab Eng Int，2005，21(8)：825-840.

［2］ Hotelling H. Multivariate Quality Control，in Techniques of Statistical Analysis[M]. New York：McGraw-Hill，1947.

［3］ Wang Taiyue，Chen Longhui. Mean shifts detection and classification in multivariate process：A neural-fuzzy approach[J]. Journal of Intelligent Manufacturing，2002，13(3)：211-221.

［4］ Hou Tung Hsu，Liu Wanglin，Lin Li. Intelligent remote monitoring and diagnosis of manufacturing processes using an integrated approach of neural networks and rough sets[J]. Journal of Intelligent Manufacturing，2003，14(2)：239-253.

［5］ Guh R S. On-line identification and quantification of mean shifts in bivariate processes using a neural networkbased approach[J]. Qual Reliab Eng Int，2007，23(3)：367-385.

［6］ Yu Jianbo，Xi Lifeng. A neural network ensemble-based model for on-line monitoring and diagnosis of out-ofcontrol signals in multivariate manufacturing processes[J]. Experts Systems with Applications，2009，36(1)：909-921.

［7］ Yu Jianbo，Xi Lifeng，Zhou Xiaojun. Intelligent monitoring and diagnosis of manufacturing processes using an integrated approach of KBANN and GA[J]. Computer in Industry，2008，59(5)：489-501.

［8］ Cheng C S，Cheng H P. Identifying the source of vari-ance shifts in the multivariate process using neural networks and support vector machines[J]. Expert Syst Appl，2008，35(1)：198-206.

［9］ Shao Y，Lu C J，Wang Y C. Determination of the fault quality variables of a multivariate process using independent component analysis and support vector machine[J]. Advances in Data Mining：Applications and Theoretical Aspects，2010，6171：338-349.

［10］ Venkatasubramanian V，Rengaswamy R，Kavuri S N，et al. A review of process fault detection and diagnosis(Part Ⅲ)：Process history based methods[J]. Computers and Chemical Engineering，2003，27(3)：327-346.

［11］ Bersimis S，Psarakis S，Panaretos J. Multivariate statistical process control charts：An overview[J]. Qual Reliab Eng Int，2007，23(5)：517-543.

［12］ Vapink V N. An overview of statistical learning theory[J]. IEEE Transactions on Neural Networks，1999， 10 (5)：988-999.

［13］ Lou Der Chyuan，Liu C L，Lin C L. Message estimation for universal steg analysis using multi-classification support vector machine[J]. Comput Stand Inter，2009，31(2)：420-427.

［14］ Burges C J C. A tutorial on support vector machines for pattern recognition[J]. Data Min Knowl Disc，1998，2(2)：121-167.

［15］ Hsu Chih Wei，Lin Chih Jen. A comparison of methods for multiclass support vector machines[J]. IEEE Transactions on Neural Networks，2002，13(2)：415-425.

［16］ Eberhart R，Kennedy J. A new optimizer using particle swarm theory[C]//Proceedings of the 6th International Symposium on Micro Machine and Human Science. Nagoya，Japan，1995：39-43.

［17］ Ranaee V，Ebrahimzadeh A，Ghaderi R. Application of the PSO-SVM model for recognition of control chart patterns[J]. ISA Transactions，2010，49(4)：577-586.

Support Vector Machine Based on Particle Swarm Optimization for Monitoring Mean Shift Signals in Multivariate Control Charts

Zhao Yongman1,2，He Zhen1，He Shuguang1，Zhang Min1
(1. School of Management and Economy，Tianjin University，Tianjin 300072，China；2. School of Mechanical and Electrical Engineering，Shihezi University，Shihezi 832000，China)

To detect the variable shifts causing out-of-control signals in multivariate control chart, this paper proposes a model of support vector machine (SVM) monitoring the mean shifts of multivariate control charts based on particle swarm optimization (PSO) algorithm. Under the assumptions that the variance matrix is constant, T2control chart is used to monitor the multivariate process. Based on different mean shift patterns, the sample data are generated. Finally, the optimized model is attained after the parameters of SVM are optimized using PSO. The simulation comparative studies show that the classification ability of the proposed SVM-PSO method outperforms that of the SVM based model and artificial neural network (ANN) based model. The classification rate of the proposed method is higher than 85%.

multivariate control chart；mean shift diagnosis；particle swarm optimization algorithm；support vector machine

TP206.3

A

0493-2137(2013)05-0469-07

DOI 10.11784/tdxb20130515▋▋

2011-11-30；

2012-05-07.

国家自然科学基金重点资助项目(70931004)；国家自然科学基金资助项目(71002105)；国家自然科学基金青年基金资助项目(70802043).

赵永满（1979— ），男，博士，讲师，zhrym@163.com.

何 桢，zhhe0321@163.com.