非完整约束系统的正则对称性*

李爱民 江金环(北京工业大学,北京 100022)

非完整约束系统的正则对称性*

李爱民 江金环
(北京工业大学,北京 100022)

本文研究了非完整约束正规Lagrange量系统在相空间中的对称性质,导出了该系统的正则方程与正则Noether定理;对非完整约束奇异Lagrange量系统,在考虑非完整约束与系统的固有约束相容的基础上,分析该系统在相空间中的对称性质,导出了该系统的正则方程与正则Noether定理。建立了非完整系统的一个积分理论,并对这两种系统分别举例,求出了相应的运动守恒量。

附加非完整约束;奇异Lagrange量;相空间;正则对称性

0 引言

一个动力学系统所受到的附加(外在)约束除由几何约束及可积分的微分约束外,还可受到不能积分的微分约束,这样的系统就叫非完整系统,该系统受到的附加(外在)不能积出的微分约束就叫做非完整约束。由于非完整约束系统动力学方程的积分十分困难,甚至系统的运动微分方程不可积,因此,对该系统运动守恒量的研究对了解该系统的物理状态和运动就更加重要。非完整约束奇异系统不仅受非完整附加(外在)约束,而且由于描述该系统运动的Lagrange量奇异而导致相空间还存在固有(内在)约束[1],因而研究其相空间的对称性与守恒量的关系就更加复杂,也更加有意义。

对非完整约束正规Lagrange量系统,非完整约束结合正则动量的定义,可化为正则变量的函数,本文先分析该系统在相空间中的对称性质,导出了该系统的正则方程与正则Noether定理;对非完整约束奇异Lagrange量系统,在考虑非完整约束与系统的固有约束相容的基础上(即非完整约束能化为正则变量 的函数,且出现在相空间的附加约束与固有约束相容),分析该系统在相空间中的对称性质,导出了该系统的正则方程与正则Noether定理,这实际上给出了非完整系统的一个积分理论。并对这两种系统分别举例说明,求出了相应的运动守恒量。

1 正规Lagrange量系统

对非完整约束正规Lagrange量力学系统,设描写系统的Lagrange量为L),其中广义坐标为qi(i=1,2,…,n),且系统所受的非完整外在约束记为

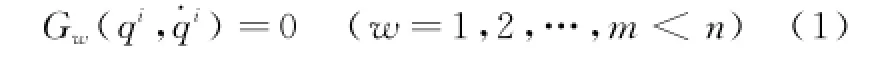
位形空间该系统的运动方程(ЧeTaeB型)为

利用Legendre变换,引入正则共轭动量[2]

对受非完整约束并用正规Lagrange量描述的广义力学系统,考虑增广相空间中有限李群下的整体无穷小变换[4]

在(12)式的变换下,假设系统的正则作用量

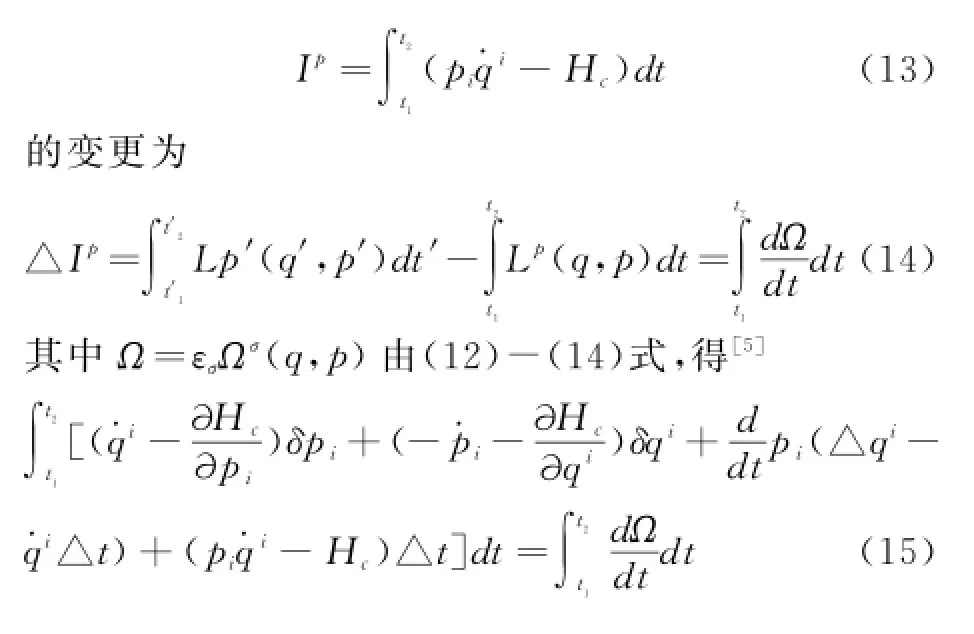
假设变换(12)式所确定的等时变分δqi=△qi-△t适合下列条件

那么,用λw(t)乘(16)式后与(15)式合并,有

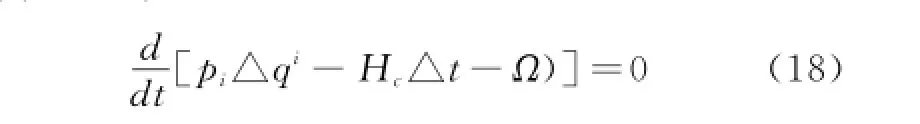
由于李群参数εσ独立,从而得

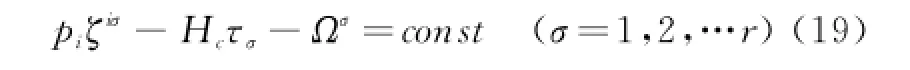
这就得到非完整约束力学系统相空间的正则Noether定理:如果变换(12)式所确定的等时变分δqi适合(16)式(即约束加在虚位移上的条件),且系统的正则作用量在(12)式变换下适合(14)式,那么,该系统在相空间中存在r个正则形式的守恒量(19)式。

例1.一力学系统的Lagrange量为

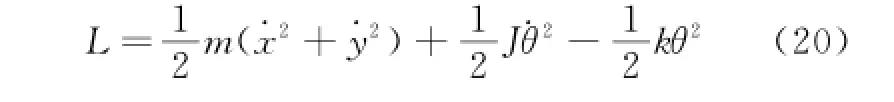
利用系统的正则方程(11)式,即沿着系统运动的轨线,由(17)得

非完整约束条件为

其中J,k为常数,x,y,θ为坐标参数[6]。

显然时间平移变换下,系统的Lagrange量(20)式和非完整约束(21)式不变,从而(14)式中的,Ω= 0,此时变换(12)式中注意到(21)式是广义速度的齐次函数,δG,因而时间平移变换满足(16)式,由(19)式得到系统的能量守恒,

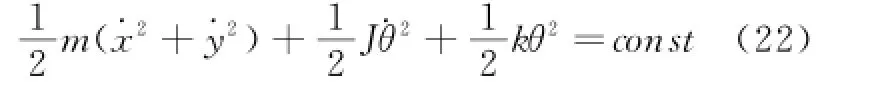
这与用其他方法求得的结果相同[8]。

2 奇异Lagrange量系统

对非完整约束奇异Lagrange量系统,设描写系统的Lagrange量为

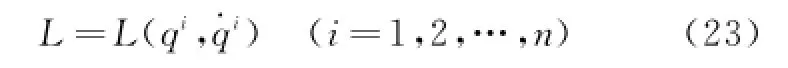
且系统所受的附加非完整约束记为

由于Lagrange量的奇异性,该系统在相空间还存在固有(内在)约束[9],设决定系统运动方程的固有约束记为

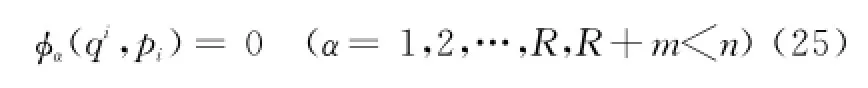
设内在约束在等时变分下适合

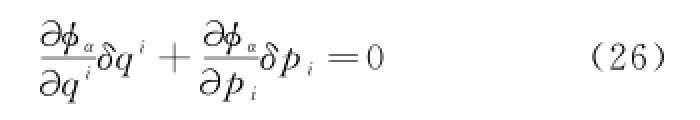
将(10)和(26)式联合,得非完整约束奇异系统的运动方程为

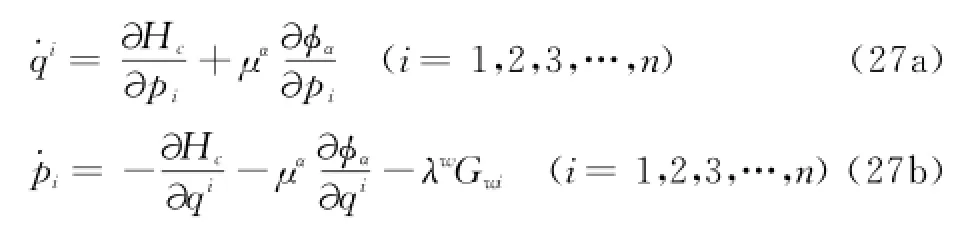
此时假定外在约束Gw=0,与内在约束φα=0,是相容,且由(3)式可解出的˙qi代入(24)式后,可化为正则变量qi,pi的函数可用正则变量qi,pi来表达。在此假设下,联合(17)式和(26)式,并利用(27)式,可得非完整约束奇异Lagrange量系统相空间的正则Noether定理:如果在(12)式变换下,系统的正则作用量的变更适合(14)式,且变换(12)式所确定的等时变分适合(16)式和(26)式,那么,此非完整约束奇异Lagrange量系统在相空间中存在r个正则形式的守恒量(19)式。

例2.一动力学系统的Lagrange量为[10]

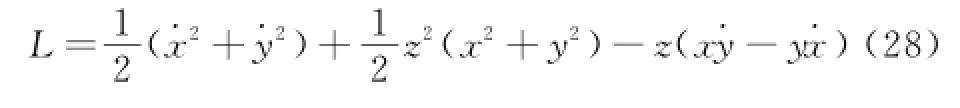
所受的附加非完整约束为

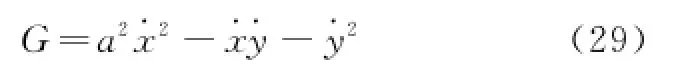
其中a为常数。

正则动量分别为

固有约束为

正则Hamilton量为

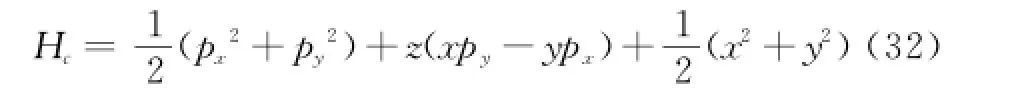
显然在时间平移变换下,系统的Lagrange量(28)式和非完整约束(29)式(可用正则变量表达)不变,时间平移变换下,变换(12)式中τσ=1,ζiσ=0,ηiσ=0。注意到(29)式是广义速度=的二次齐次函数,因此,时间平移变换下,δqi分别满足(16)式和(26)式,按(19)式,此非完整约束奇异Lagrange量系统存在能量守恒

3 结论

非完整约束奇异Lagrange量系统,在一定条件下,即非完整约束中出现的˙qi由正则动量的定义,可用来替代qi,pi且出现在相空间的附加约束与固有初级约束相容,此时对系统的描述可过渡到相空间形式,研究其正则对称性。本文对非完整约束系统正则对称性的研究,实际上给出了非完整系统的一个积分理论。当所研究的系统可转化为一个约束Hamilton系统,由正则约束随时间演化的稳定性,进一步可求出相空间的次级约束,从而,可研究该系统的量子化。

[1][4]Li A M,Jiang J H ,Li Z P.Canonical symmetry properties of constrained singular generalized mechan ical system[J].Chin.Phys,2003,(12):467-471.

[2][3]Li Z P,Jiang J H.Symmetries in constrained can onical systems[M].Beijing:Science Press,2002:35 -36.

[5]李子平.约束哈密顿系统及其对称性质[M].北京:北京工业大学出版社,1999:170.

[6]梅凤翔.非完整力学基础[M].北京:北京工业学院出版社,1987:78.

[7]李子平,李爱民.约束系统的量子对称性质[M].北京:北京工业大学出版社,2011:322.

[8]李子平.约束系统的变换性质[J].物理学报,1981, (12):1559-1671.

[9]李子平.约束系统正则形式的对称性质[J].物理学报, 1992,(5):710-719.

[10]Li Z P,Wu B C.Symmetry in extended phase space for singular Lagrangian systems with subsidiary constraints[J].Int.J.Theor.Phys,1994,(33):1063-1075.

O412.3;O413.3

A

1672-9846(2013)03-0068-03

2013-07-22

国家自然科学基金项目“约束奇异系统的量子理论及其在凝聚态等领域的应用”(编号:10647102);北京工业大学博士科研启动基金项目“约束奇异系统量子水平的变换性质及应用”(编号:52006015200701)。

李爱民(1964-),女,湖南临湘人,北京工业大学应用数理学院副教授,博士,主要从事经典与量子约束奇异系统的基本理论及应用研究。

江金环(1973-),女,河北邢台人,北京工业大学应用数理学院讲师,博士,主要从事量子场论研究。