网络统计——复杂网络基础问题：为标度律提供统计支持

陈庆华，史定华

(1. 福建师范大学 福州 350007; 2. 上海大学数学系 上海 宝山区 200444)

复杂网络科学[1]和与之相关的人类动力学[2]发现，许多复杂现象存在令人惊奇的普适规律，即涌现标度特性。例如，复杂网络的度分布呈现P(k)～k−γ的幂律形式，人类时空行为往往阵发而非随机，导致任务等待时间也呈现这一形式。物理学家侧重探索它们形成的动力学机制，如增长择优连线或任务优先权规则等。然而确认标度律是否成立还同时需要得到广泛的统计支持。文献[3]就用一幅图展示了标度律的两大支柱：机制成熟和统计支持的景观。

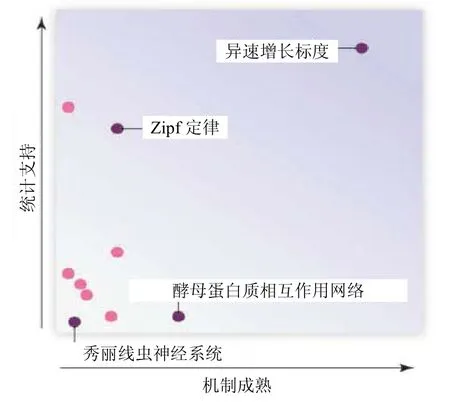
图1 统计支持

统计学是一门古老的学科，也是统计物理的基础，取得了许多重要成果，有着广泛的实际应用。在我国高校，统计学已列入一级学科，人才供不应求。科学出版社出版的《统计手册》[4]有百余万字厚达千页，但却没有涉及标度律的统计方法。究其原因主要是定义不够明确，幂律形式是指近似幂律关系，严格幂律分布还是重尾分布，认识并不统一。

网络科学刚刚出现时，人们普遍采用简单的图估计方法进行统计。而且主要是在双对数坐标上画频率图，看上去基本成一条直线就认为服从标度律。由于大度数节点稀少，尾部摆动太大，就采用粗粒化的对数盒子图。在确定几何增长网络度分布指数时出现了反复，人们才开始使用画补分布图。关于这三种图的画法与比较，详细讨论参见文献[5]。画补分布图实质上等价于画秩次图，秩次图早在研究人类语言规律时就已被采用。Zipf在研究文本中单词出现频次时，将所有单词排序，用横坐标表示序号，纵坐标表示对应的频次，在双对数坐标上画图得到了著名的Zipf标度律。文献[6]用两套数据比较了频率图和秩次图的优劣，数据1和数据2分别从幂律分布和指数分布产生，并分别画在双对数坐标和半对数坐标上，他们发现按秩次画图正确，按频率画图会出现错误。可见正确统计方法的重要性。

图估计方法全凭经验，结果因人而异。现在考虑数值方法，对于严格连续幂律分布：

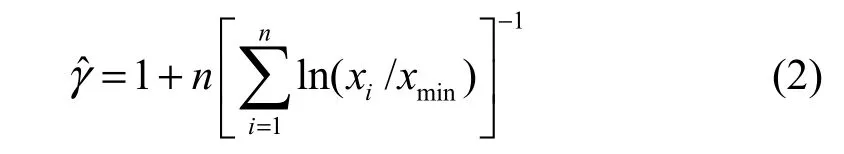
这是参数γ的极大似然估计，它是有偏估计，因为。文献[8]证明了针对连续幂律分布不存在有效无偏估计，只存在渐近有效无偏估计：

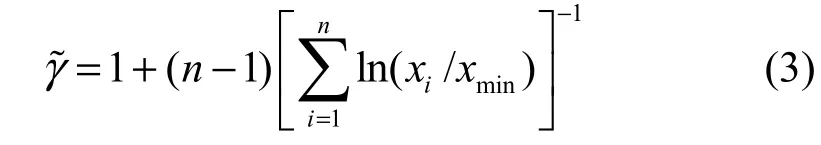
进一步，文献[8]还讨论了假设检验和似然比检验。引入连续伽玛分布

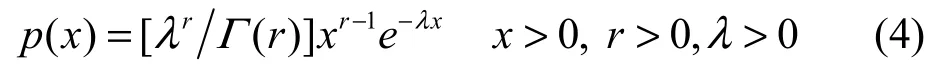
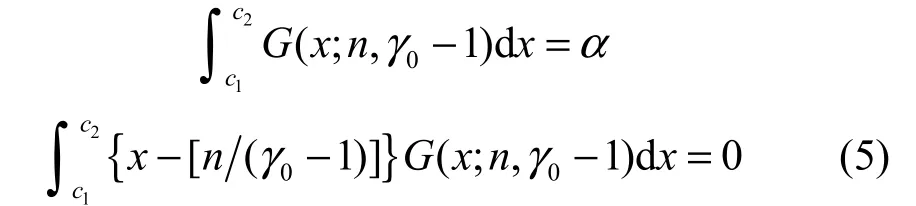
然而，复杂网络中的度是离散的，上述估计结果需修正。另外，实际网络的最小度也是随机变量，而且对估计结果有重要影响。前面的讨论都是假定实际网络的度分布服从幂律分布，而这是需要统计检验的。更为重要的是度分布往往不是严格幂律的，而是重尾分布。重尾分布是一个很大的分布类，严格幂律分布只是其中最简单的代表。文献[9]发现Waring分布为：

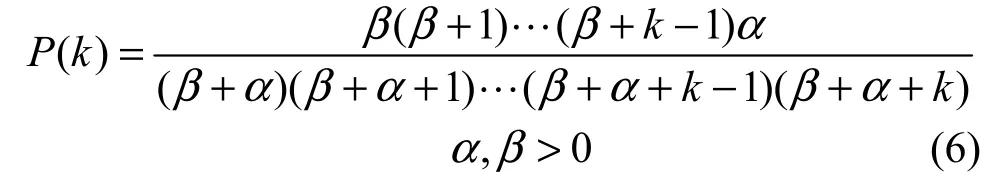
是另一个重要代表，几乎所有无标度增长网络模型的度分布都是Waring分布。如BA模型度分布是α=2，β=m；复制模型入度分布是α=1，β=1的Waring分布。因此，深入研究双参数Waring分布的统计分析方法具有重要的理论意义和实际价值。

[1] BARABÁSI A-L, ALBERT R. Emergence of scaling in random networks[J]. Science, 1999(286): 509-512.

[2] BARABÁSI A-L. The origin of bursts and heavy tails in human dynamics[J]. Nature, 2005(435): 207-211.

[3] STUMPF M P H, PORTER M A. Critical truths about power laws[J]. Science, 2012(335): 665-666.

[4] 茆诗松, 王静龙, 史定华, 等. 统计手册[M]. 北京: 科学出版社, 2003.MAO Shi-song, WANG Jing-long, SHI Ding-hua, et al.Statistical handbook[M]. Beijing: Science Press, 2003.

[5] 史定华. 网络度分布理论[M]. 北京: 高等教育出版社,2011.SHI Ding-hua. Theory of network degree distributions[M].Beijing: Higher Education Press, 2011.

[6] LI L, ALDERSON D, DOYLE J C, et al. Towards a theory of scale-free graphs: definitions, properties, and implications[J]. Internet Math, 2005(2): 431-523.

[7] CLAUSET A, ROHILIA S, NEWMAN M E J. Power-law distributions in empirical data[J]. SIAM Review, 2009(51):661-703.

[8] 陈庆华, 陈月萍, 史定华. 幂律分布的统计性质及其应用[C]//第八届全国复杂网络学术会议. 南京: [出版者不详],2012.CHEN Qing-hua, CHEN Yue-ping , SHI Ding-hua. The statistic property of power-law distributions and its applications[C]//The 8th Chinese Conference on Complex Networks. Nanjing: [s.n.], 2012.

[9] 史定华. 关于无标度网络[C]//第八届全国复杂网络学术会议. 南京: [出版者不详], 2012.SHI Ding-hua. About scale-free networks[C]//The 8th Chinese Conference on Complex Networks. Nanjing: [s.n.],2012.