改进的Louvain社团划分算法

吴祖峰，王鹏飞，秦志光，蒋绍权

(电子科技大学计算机科学与工程学院 成都 611731)

在研究复杂的社会、技术以及信息系统时，常把这些系统描述成网络。在这样的关系网络中，节点代表一个成员，而边代表成员之间的关系[1]。社团划分是指根据网络的属性特征把关系网络中各个节点划分到各个具有特殊含义的社团中。社团是指在其内部点之间的连接很紧密。而在社团之间的连接相对比较松散。通过将社会生活中的关系网络抽象成计算机能够表示的图，之后运用社团划分算法，根据图的某种特性将图划分成一个个子图(即社团)。

现实中的网络不同于一个随机网络，它有很强的结构特征。所以可以根据其结构特征进行社团划分。随着社会的发展，人与人之间的关系越来越密切，现实生活中各种关系网络也在不断扩大，其复杂程度也日益加大。人与人之间的关系网络包含了很多有意义的特性，依据这些特性可以把网络进行划分，从而便于理解网络的结构情况，以服务于我们的生活、工作、商业、国防等。

网络划分的算法有很多种，主要分为以下两种：一种是分离法，找出社团之间的边把它们从网络中移除[2-3]；一种是聚合法，将联系紧密的点聚合为一个社团[4-5]，并通过优化某个相关变量的函数来实现聚合[6-7]。

根据两类划分算法的结果分析，聚合算法比分离算法好，且聚合算法的效率也相对较高。由于这些原因，聚合算法吸引了很多学者做了大量相关研究。文献[4]提出了一个基于模块属性的测量方法。文中引入了一个变量，该变量被称作模块度，用于衡量社团划分结果的合理性。其原理是用某种划分结果的模块内聚性与随机划分结果的内聚性的差值对划分结果进行评测。因为要找到最优的模块性划分是一个相当困难的问题[8]，所以基于模块度的社团划分算法的研究仍然在继续。该模块度对后来的社团划分有很重要的影响，很多有影响的算法都是基于该特性进行算法设计的。随后，文献[9]提出了一个新的算法，采用贪心算法对模块度函数进行求解，得到了近似最优结果。通过将测量公式运用于划分算法，并利用模块度增量[9]，使社团划分的算法效率大大提高。但是用该算法处理大型复杂网络时，其所消耗的计算时间相当长。文献[10]提出了基于模块度的一个快速算法——Louvain算法。该算法可以快速处理具有数以亿计节点的网络，用模块性对社团划分的质量进行衡量，其值位于−1到1之间[2,11]。如果模块性的值越大，说明社团划分的质量越高。

本文的算法就是基于这个算法改进而来的。在现实网络中常常会有很多叶子节点。特别是对于层级结构比较突出的网络。所谓叶子节点就是指其只有一条边与其他点相连，也属于一种边缘节点。该情况更多的会出现在等级分层的现实网络中，如行政机关、学校、公司等等，但是这些情况在原算法中并未考虑，而叶节点是可以利用剪枝处理来加快处理速度。改进算法通过对叶节点进行剪枝处理，从而提高算法的处理速度。

1 算法思想

1.1 思想描述

Louvain算法是基于模块性的算法，在一个有权的网络中，模块性的定义为：

式中，Aij表示连接节点i与j边的权值；Ki表示和节点i相连的边的权值之和；ci表示i所属的社团。∂(u,v)表示u与v是否为同一个社团，如果u与v为同一个社团此值为1，否则为0；

不断遍历网络中的点，将其从原来的社团取出，计算该点加入到各个社团产生的模块性增量，从这些社团中挑选一个对应模块性增量最大的社团，把该点加进去，直到没有点可以移动，将各个社团合并成一个超点。重复上述步骤，直到模块性不再增加[10]。模块性增量是指将一个点从原来的社团取出加入另一个社团后，模块性的值发生变化，有：

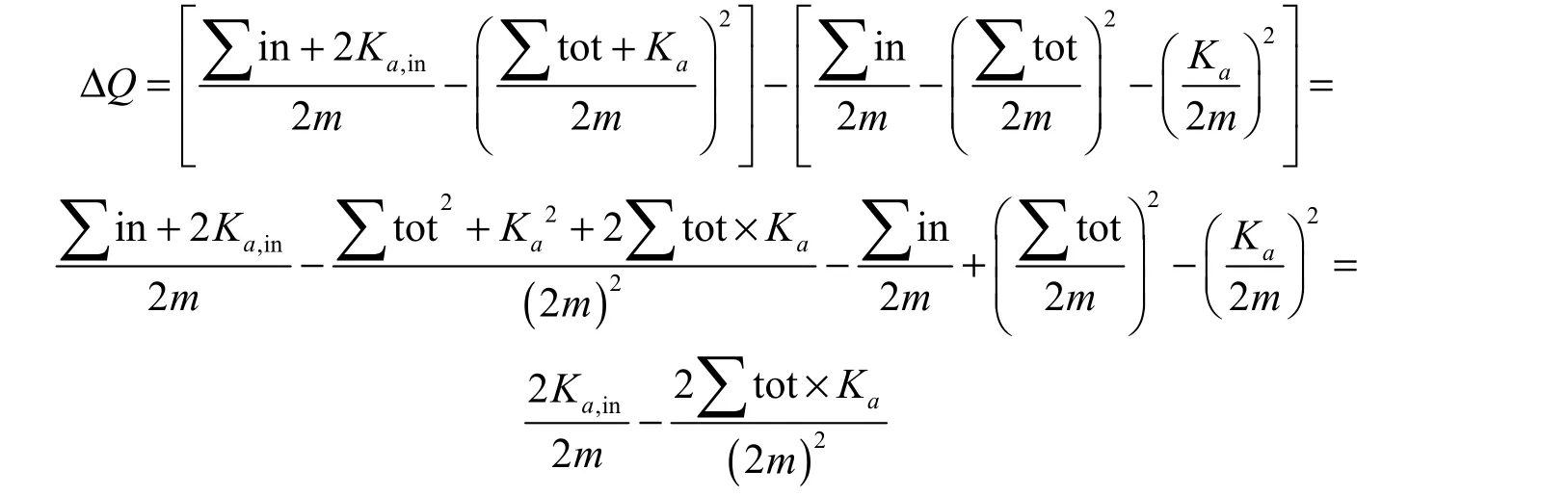
式中，∑in表示在社团C中的所有边权值之和；C表示指点a要加入的社团；a表示将要移动的节点；表示i点到C的所有边的权值之和；∑tot表示所有连接到社团C的边的权值之和。

叶子节点只和一个其他节点相连接。而划分结果是要避免单独节点归属于一个社团，除非该节点是孤点(没有边)。因此对于叶节点来说，其必然要划归到与其相连点所在的社团中，所以相关的很多运算可以避免。如可以不用计算ΔQ而直接将叶节点移入到相应的社团，从而使算法的效率提高。带叶节点的网络如图1所示，图中，黑色节点有3个叶节点，在Louvain算法中要对这3个叶节点分别进行处理，而在改进算法中直接将其划归于黑色节点所在的社团。通常叶节点只在第一层划分的时候存在，而一旦形成超点后就不再有叶节点了。所以改进算法是对算法的第一层划分进行改进。第一层划分处理的数据量是最大的。随着层数的增高，节点数也随之减少。所以改进后的算法的明显提高了算法效率。

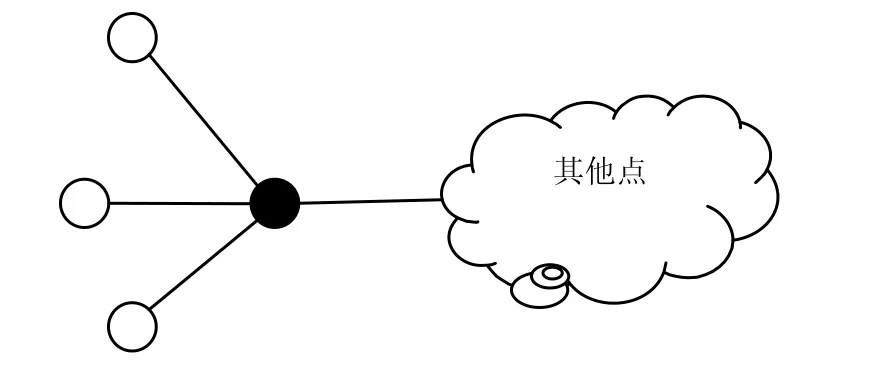
图1 带叶节点的网络

Louvain算法主要分为两个步骤：1) 将各个节点不断的在各个社团中迁移，直到所有模块度增量不再为正值；2) 将各个社团合并成一个超点。这两个步骤运行的结果产生一个层级，层级不断提高，直到模块度的值不再增加，算法结束。改进算法就是在第一步中迁移节点的时候加入剪枝判断，如果为叶节点，将后来的所有运算跳过，直接将该点从原社团移入该点邻接点所在的社团中。

1.2 改进后的算法的伪代码

为了更好地理解改进后的算法，给出了算法的伪代码。改进的Louvain社团划分算法为：

输入 用邻接表表示的网络图G(V，E)

输出 对进行G(V，E)划分后的结果

2 实验结果与分析

为了验证算法的有效性，分别用改进算法和Louvain算法处理了18组程序生成的数据集和某个机构一周内的邮件数据集。通过对比运行结果，发现改进算法有比较明显的优势。

改进算法在处理叶节点较多的网络时优势比较明显，对应于现实关系网络，层级结构比较明显的网络叶节点往往比较多。因此，本文根据层级结构的特征，用程序生成了18组实验数据集。每组数据集中包含了约500 000个节点。18组数据集中的叶节点所占的比重不同。

图2显示了改进后算法比Louvain算法效率有提升。竖轴的百分比(1−改进后算法运行时间/原始算法运行时间)。当数据集的叶节点数量所占总节点数量的百分比低于10%的时候，改进算法的优势体现的不是很明显。当叶节点数量达到20%的时候改进算法相对于Louvain算法所用时间减少了0.706%。当叶节点数量达到30%的时候改进算法相对于Louvain算法所用时间减少了1.324%。当叶节点数量达到40%的时候改进算法相对于Louvain算法所用时间减少了2.083%。当叶节点数量到50%的时候改进算法相对于Louvain算法所用时间减少了2.736%。当叶节点数量达到60%的时候改进算法相对于Louvain算法所用时间减少了4.081%。同时计算了改进算法和Louvain算法划分结果的模块度，发现两种结果所得出的模块度的值完全一样。所以改进算法相对于Louvain算法并没有改变划分结果的准确度。

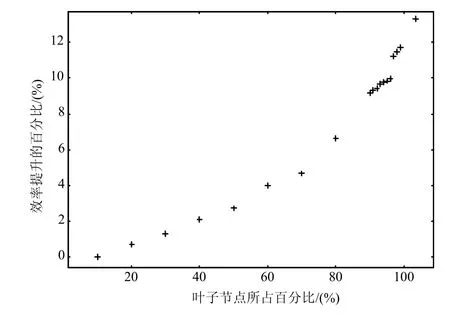
图2 改进前后算法对比结果

为了验证改进算法对于实际网络有同样的效果，本文采集了某个机构一周内收发的邮件。用该邮件数据形成一个网络，发件人和收件人用节点表示，邮件用边表示。在该邮件网络中，有23 671个节点和306 184条边。分别用改进算法和原始算法对该网络数据进行处理，结果发现改进算法相对于原始算法所用时间减少了3.931%，且两者划分出的社团的模块度完全一致。所以本文算法在现实社交网络中相对于Louvain算法仍有明显的优势。

3 总 结

由于改进后的算法主要是对叶子节点进行优化，更适合用于处理叶子节点比较多的网络。在对网络处理的初期，会有很多叶子节点，在第一次进行社团划分的时候用改进算法，随着超点的形成，再采用Louvain算法。

以上只是对算法运行结果的第一层进行了改进。到达第二层时由于每个超点都包含多个节点，所以每个超点相对于原图来说，都不是叶节点，因此不能使用改进的算法。但是对于一些网络，可以预测或者人为规定它划分出的每个社团的节点个数不会少于某个值N时，可以对算法每一层都进行改进。只要某个叶子超点内的节点数不超过N，就可以将其直接划归到其邻居节点所在的社团中，特别是在一些等级比较严格的网络，在处理的过程中随着每一层中低级叶节点的消失，同时新的叶子超点在不断的出现，这样改进算法仍然可以使用，从而进一步提高了效率。

[1] NEWMAN M E J, BARABASI A L, WATTS D J. The structure and dynamics of networks[M]. Princeton, USA:Princeton University Press, 2006.

[2] GIRVAN M, NEWMAN M E J. Improved spectral algorithm for the detection of network communities[J]. Proc Natl Acad Sci USA, 2002(99): 7821-7826.

[3] RADICCHI F, CASTELLANO C, CECCONI F, et al.Defining and identifying communities in networks[J]. Proc Natl Acad Sci USA, 2004(101): 2658-2663.

[4] NEWMAN M E J, GIRVAN M. Finding and evaluating community structure in networks[J]. Phys Rev E, 2004,69(2): 026113-1-026113-15.

[5] CLAUSET A, NEWMAN M E J, MOORE C. Finding community structure in very large networks[J]. Phys Rev E,2004, 70(6): 066111-1-066111-6.

[6] WU F, HUBERMAN B A. Finding communities in linear time: a physics approach[J]. Phys J B, 2003, 38(2): 331-338.

[7] NEWMAN M E J. Finding community structure in networks using the eigenvectors of matrices[J]. Phys Rev E, 2006,74(3): 036104-1-036104-19.

[8] BRANDES U, DELLING D, GAERTLER M, et al.Maximizing modularity is hard[EB/OL]. [2010-05-20].http://arxiv.org/abs/physics/0608255.

[9] NEWMAN M E J. Fast algorithm for detecting community structure in networks[J]. Phys Rev E, 2004, 69(6):066133-1- 066133-5.

[10] VINCENT D B, GUILLAUME J L, RENAUD L, et al.Fast unfolding of communities in large network[J]. Journal of Statistical Mechanics: Theory and Experiment, 2008(10):1-12.

[11] NEWMAN M E J. Modularity and community structure in networks[J]. Proc Natl Acad Sci USA, 2006(103): 8577-8582.