基于压缩感知的MIMO-OFDM系统稀疏信道估计方法
2013-01-08王妮娜苏泳涛石晶林
王妮娜,桂 冠,苏泳涛,石晶林 ,张 平
(1. 中国科学院计算技术研究所 北京 海淀区 100190; 2. 移动计算与新型终端北京市重点实验室 北京 海淀区 100190;3. 北京邮电大学信息与通信工程学院 北京 海淀区 100876; 4. 电子科技大学电子工程学院 成都 611731 )
无线通信技术的快速发展,使得正交频分复用(OFDM)技术和多输入多输出(MIMO)技术很快成为下一代移动通信系统的关键候选技术[1-2]。OFDM系统具有频率利用率高、有效抵抗多径干扰和窄带干扰等优点[3];MIMO技术能有效提高系统容量和系统分集。在无线频谱资源异常稀缺的下一代通信环境中,二者的结合是提高频谱资源利用率和对抗信道频率选择性衰落的有效方法之一。纵然MIMO-OFDM系统具有诸多优点,然而在具体实际应用中,仍然面临很多问题。OFDM系统对同步误差甚为敏感,在信号传输过程中,由于信号受周围环境及障碍物影响,产生不同程度地衰落和时延,时间同步误差会造成符号间干扰(inter symbol interference,ISI),频率同步误差会产生子载波间干扰(inter carrier interference,ICI)。另外,由于支持多天线技术,符号间干扰和码间干扰更加严重,从而验证影响系统性能[4]。因此,接收端需要获得精确的信道状态信息(CSI),精确的信道估计起到尤为重要的作用。只有对信道特征有很好的了解,才能有效克服干扰和失真。CSI的准确性直接影响无线通信系统的整体性能,因此信道估计是可靠的无线通信系统中核心环节[5-6]。
传统的线性信道估计方法,如LS算法[7]和MMSE算法[8]等,均基于多径信道密集型假设,没有挖掘实际通信信道具有的潜在的稀疏性,因此需要利用比整个信道变量更多的导频信号资源才能准确地估计信道,但会导致频谱资源利用率降低。
近年来,越来越多的物理信道测量发现,无线宽带多径信道呈现稀疏特性,即大部分能量集中在很少抽头上,而很小一部分能量集中在大多数信道抽头上,因此低于噪声门限[9-12]。换言之,充分利用信道的稀疏性这一先验信息,就能利用较少的导频符号,得到理想的信道估计效果,从而提高频谱资源利用率。通过挖掘信道的稀疏特性,文献[13]提出一种基于匹配追踪(matching pursuit,MP)算法的稀疏信道估计方法,通过计算机仿真验证稀疏信道估计的有效性,但是MP算法却不是很稳定。文献[14]提出了正交匹配追踪(OMP)[15]的稀疏信道估计算法,进一步提高了估计精度,然而忽略了计算复杂度的改善和在多天线系统中的应用。随着压缩感知理论在应用数学和信号处理领域的广泛深入研究[16-19],如何运用压缩感知进行稀疏信道估计成为目前研究的热点[20-22]。
本文的贡献是将压缩感知中的CoSaMP重构算法[23]应用于MIMO-OFDM系统的稀疏多径信道估计。该算法通过利用多径信道具有的稀疏特性,以很小的计算复杂度为代价,使用比传统线性算法少得多的导频数目,得到较高的信道估计精确度,即以非常小的计算复杂度为代价换取较高的信道估计精度和频谱资源利用率;此外,本文还证明CoSaMP算法相比其他常用压缩感知重构算法具有更小的计算复杂度,是压缩感知理论重构算法在信道估计应用中的极佳候选。
1 MIMO-OFDM系统模型
MIMO-OFDM系统模型如图1所示,假设发射天线数为NT,接收天线数为NR,子载波个数为K。第m个发送天线与第n个接收天线之间的多径信道时域响应函数表示为:
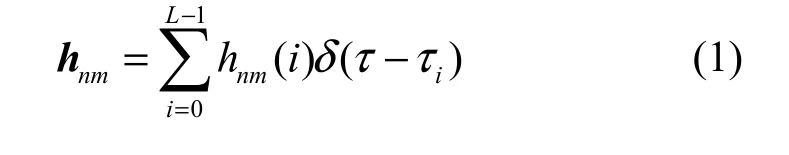

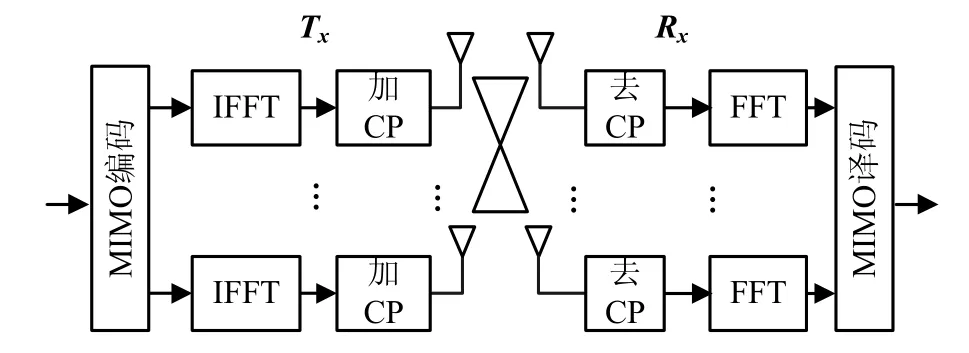
图1 MIMO-OFDM系统模型


2 稀疏多径信道估计
2.1 压缩感知综述
压缩感知在已知信号稀疏或可压缩的情况下直接获取或重构信号的过程,近期在应用数学和信号处理领域受到了广泛的关注,并且广泛应用于图像处理、雷达、语音识别、数据捕获等领域[20]。其基本的测量模型表示为:
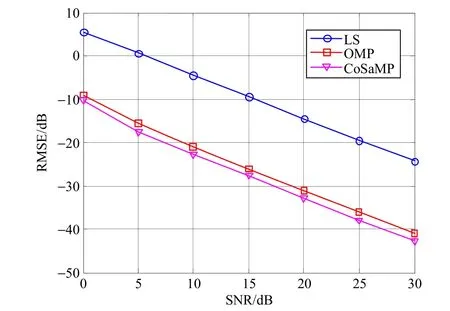
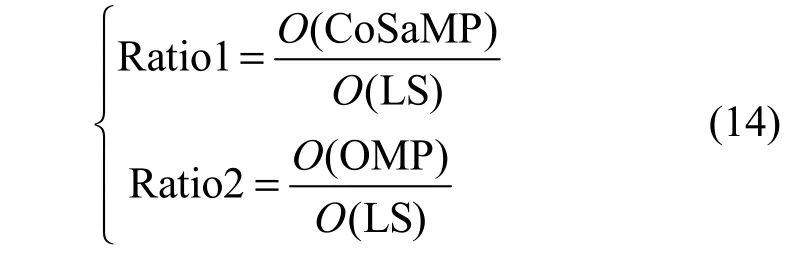
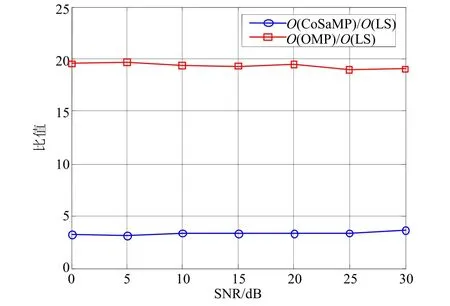
式中,X表示M×N维已知的测量矩阵(M 为了使测量矩阵X满足受限等距特性RIP,需要从导频输入输出关系着手研究。文献[22]给出了一种MIMO-OFDM系统随机结构导频测量矩阵满足等距性条件RIP约束的证明。 CoSaMP-SCE方法是以压缩感知为理论背景,借助应用数学领域中先进的CoSaMP重构算法,应用于MIMO-OFDM系统的信道估计方法。已知系统发送天线数为NT、接收天线数为NR、任意接收/发送天线间信道的稀疏度为T、子载波数目为K、接收的导频符号为y、发送的导频符号为X,信道模型如式(5)所示,CoSaMP-SCE方法的具体步骤如下: 1) 算法初始化。 迭代次数i=1;残差向量r0=y;初始信道抽头系数索引集0Ω=∅; 2) 迭代过程(第i次迭代步骤)。 本文通过对比传统LS算法、OMP稀疏信道估计算法(简记OMP)和CoSaMP稀疏信道估计算法(简记CoSaMP)的信道估计性能,采用均方根误差(root mean square error, RMSE)量化信道估计误差。RMSE值αRMSE的表达式为: 式中,M为蒙特卡洛仿真次数。可以看出,RMSE值越小,信道估计越准确。在仿真中,假设系统为子载波个数为1 024的2×2的MIMO-OFDM系统,其中导频子载波个数NP为56。假设信道参数在一个OFDM符号里是恒定的,信道长度L为32,其中非零抽头个数T为5,非零抽头位置随机分布,如图2所示。 图3为信噪比为0~30 dB情况下,LS、OMP和CoSaMP的RMSE表现性能统计。可以看出,3种算法信道估计误差随着SNR的增大而逐渐减小,即SNR越大,信道估计越精确;在相同的SNR下,对于相同数目的导频符号,CoSaMP的信道估计性能较OMP有所提高,且二者明显比LS性能优越。换句话说,CoSaMP算法用更少的导频符号能达到与LS相比拟的信道估计性能。 图2 稀疏信道冲击响应在信道长度为32,非零抽头数目为5时的实部、虚部幅值 图3 均方根误差与信噪比关系变化图 信道估计需要实时反映信道状态信息,因此合理控制计算复杂度至关重要。CoSaMP与OMP算法计算复杂度在文献[23]中给出了详细分析,在本文中,OMP算法复杂度可用表示,而CoSaMP算法复杂度为为了更加直观地比较各种算法计算复杂度,用计算机的运行时间进行量化,且采用CPU运行时间的比值进行比较,即: 式中,O()为用于度量计算复杂度的符号[13]。仿真结果如图4所示,CoSaMP-SCE的计算复杂度非常接近LS(约为LS的3倍),而OMP计算复杂度大约为LS的18倍。 图4 CoSaMP算法、OMP算法分别与LS算法计算复杂度比值与信噪比变化关系对比图 本文根据实际MIMO-OFDM系统的信道特点,提出一种基于压缩感知的CoSaMP稀疏信道估计方法。理论分析和仿真结果表明:与传统线性方法相比,本文所述方法极大地提高了信道估计精确度和频谱利用率,并极大地降低了基于压缩感知理论的同类算法的计算复杂度。 [1] 张平. Beyond 3G移动通信系统关键技术[J]. 北京邮电大学学报, 2002, 25(3): 1-6.ZHANG Ping. Some research issues for beyond 3G mobile systems[J]. Journal of Beijing University of Posts and Telecommunications, 2002, 25(3): 1-6. [2] SU Yong-tao, TANG Shan, SHI Jing-lin, et al. Robust downlink precoding in multiuser MIMO-OFDM systems with time-domain quantized feedback[C]//2010 IEEE Wireless Communications and Networking Conference(WCNC). Beijing: IEEE Press, 2010: 1-5. [3] ZHOU Y, WANG J, SAWAHASHI M. Downlink transmission of broadband OFCDM systems—Part I: Hybrid detection[J]. IEEE Transactions Communications, 2005,53(4): 718-729. [4] ZHOU Y, WANG J, SAWAHASHI M. Downlink transmission of broadband OFCDM systems—Part II: Effect of doppler shift[J]. IEEE Transactions Communications,2006, 54(6): 1097-1108. [5] 王甫莉, 阔永红, 陈健, 等. MIMO-OFDM系统信道估计算法综述[J]. 电子科技, 2007, 209(2): 73-75.Wang Pu-li, KUO Yong-hong, CHEN Jian, et al. Review on the channel estimation algorithms for MIMO-OFDM systems[J]. Electronic Science and Technology, 2007,209(2): 73-75. [6] ZHOU Y, NG T S. Performance analysis on MIMOOFCDM systems with multi-code transmission[J]. IEEE Transactions on Wireless Communications, 2009, 8(9):4426-4433. [7] LI Ye. Simplified channel estimation for OFDM systems with multiple transmit antennas[J]. IEEE Transaction on Wireless Communications, 2002, 1(1): 67-75. [8] SUH C, HWANG C S, CHOIT H. Comparative study of time-domain and frequency-domain channel estimation in MIMO-OFDM systems[C]//The 14th IEEE 2003 International Symposium on Personal, Indoor and Mobile Radio Communication Proceedings. Beijing: IEEE Press,2003: 1095-1099. [9] ZHOU Yan, HERDIN M, SAYEED A M, et al. Experimental study of MIMO channel statistics and capacity via the virtual channel representation[DB/OL]. [2007-09-19].http://dune.ece.wisc.edu/pdfs/zhou_meas.pdf. [10] CZINK N, YIN X, OZCELIK H, et al. Cluster characteristics in a MIMO indoor propagation environment[J]. IEEE Trans Wireless Commun, 2007, 6(4): 1465-1475. [11] VUOKKO L, KOLMONEN V M, SALO J, et al.Measurement of large-scale cluster power characteristics for geometric channel models[J]. IEEE Trans Antennas Propagat, 2007, 55(11): 3361-3365. [12] CRAMER R J M, SCHOLTZ R A, WIN M Z. Evaluation of an ultra-wide-band propagation channel[J]. IEEE Trans Antennas Propagat, 2002, 50(5): 561-570. [13] COTTER S F, RAO B D. Sparse channel estimation via matching pursuit with application to equalization[J]. IEEE Transaction on Communications, 2002, 50(3): 374-377. [14] KARABULUT G Z, YONGACOGLU A. Sparse channel estimation using orthogonal matching pursuit algorithm[C]//IEEE 60th Vehicular Technology Conference. Los Angeles, USA: IEEE Press, 2004: 3880-3884. [15] TROPP J, GILBERT A. Signal recovery from random measurements via orthogonal matching pursuit[J]. IEEE Transaction on Information Theory, 2007, 53(12): 4655-4666. [16] DONOHO D L. Compressive sensing[J]. IEEE Transaction on Information Theory, 2006, 52(4): 1289-1306. [17] BARANIUK R G, CANDES E, NOWAK R, et al.Compressive sensing[J]. IEEE Signal Processing Magazine,2007, 24(4): 118-120, 124. [18] BARANIUK R. A lecture on compressive sensing[J]. IEEE Signal Processing Magazine, 2007, 24(4): 118-121. [19] NEEDELL D. Topics in compressed sensing[DB/OL].[2009-09-19]. http://arxiv.org/abs/0905.4482. [20] BAJWA W U, HAUPT J, SAYEED A M, et al. Compressed channel sensing: a new approach to estimating sparse multipath channels[J]. Proceedings of the IEEE, 2010,98(6): 1058-1076. [21] BAJWA W U, SAYEED A, NOWAK R. Sparse multipath channels: modeling and estimation[C]//The 13th IEEE Digital Signal Processing Workshop. Marco Island, USA:IEEE Press, 2009: 320-325. [22] TROPP J A, WRIGHT S J. Computational methods for sparse solution of linear inverse problem[J]. Proceedings of the IEEE, 2010, 98(6): 948-958. [23] NEEDELL D, TROPP J A. CoSaMP: Iterative signal recovery from incomplete and inaccurate samples[J].Applied and Computational Harmonic Analysis, 2009,26(3): 301-321. [24] BERGER C R, WANG Zhao-hui, HUANG Jian-zhong.Application of compressive sensing to sparse channel estimation[J]. IEEE Communication Magazine, 2010,48(10): 164-174. [25] CANDES E J. The restricted isometry property and its implications for compressed sensing[J]. Comptes Rendus Mathematique, 2008, 346(9): 589-592. [26] 周小平, 方勇, 汪敏. MIMO-OFDM快衰落信道的压缩感知估计方[J]. 电波科学学报, 2010, 25(6): 1109-1115.ZHOU Xiao-ping, FANG Yong, WANG Min. Compressed sensing estimation methods for fast fading channel of MIMO-OFDM systems[J]. Chinese Journal of Radio Science, 2010, 25(6): 1109-1115. [27] NEEDELL D. Topics in compressed sensing[D]. USA:University of California, 2009.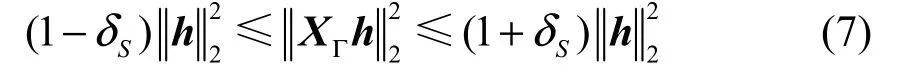
2.2 稀疏多径信道估计算法

3 仿真结果

3.1 信道估计精确度对比

3.2 计算复杂度对比
4 结 束 语
