非接触电能传输系统恒流充电控制方法研究

戴 欣，曹伟华，孙 跃

(重庆大学自动化学院 重庆 沙坪坝区 400044)

非接触电能传输技术(CPT)是一种借助于电磁场完成电能传输的新兴技术。由于摆脱了传统电气接触方式，该技术可提供一种更灵活、更安全可靠的电能接入方式[1-2]。因此，近几年来，该技术逐渐成为研究热点，并得到了广泛的应用。如电动车的充供电[3]、数码设备的充电[4]等。

随着锂电池充电应用的日趋广泛，工业界对锂电池充电过程的控制提出了更高的要求。对锂电池充电过程中，在保证电池寿命的前提下应尽可能提高电池充电速度。通常需要采用恒流充电方式。然而，实现非接触电能传输系统的恒流输出控制较复杂，这主要是因为系统是一个复杂的电磁综合系统，影响输出电流品质的因素较多，如负载参数变化、原副边的耦合参数扰动等[5]。同时，由于系统的开关拓扑切换给系统带来了严重的开关非线性[6-7]，谐振环节会导致系统存在高阶特性，这些特性都使系统建模及控制器设计较为困难。

目前，针对非接触电能传输系统的输出控制主要侧重于恒压控制方法。由于系统动力学模型的复杂性，传统恒压控制方法主要采用简单的副边独立控制，如短路解耦法[8]、动态调谐法[9-13]等。这些方法皆采用不依赖系统模型的Bang-Bang控制方法，其控制设计简单且易于实现，但控制精度及对参数变化的鲁棒性能却受到一定的影响，并且无法根据负载情况动态控制原边激磁能量输入，导致系统在轻载时效率急剧下降。文献[14-15]提出一种基于原边控制的主动控制方法，该方法根据不同负载情况控制原边能量输入，不但可以简化副边结构，而且可以根据负载需求实现按需供能，但控制器设计同样受到模型复杂性及高阶性的限制。

针对非接触电能传输系统充电过程的控制，本文提出一种基于H∞范数的恒流输出控制方法。该方法是一种原边主动控制方法，通过将系统模型在频域进行展开及非线性开关函数的傅里叶变换，得到系统的状态空间平均模型(generalized state space averaging，GSSA)。基于该模型，系统建立性能加权函数构建系统的被控向量，又基于线性分式描述的系统模型，分别建立控制器及观测器的Ricatti方程，并通过Hermitian矩阵完成该方程的求解。在此基础上，本文建立了一种迭代方法以获得最优的H∞控制器，实现对输出电流的恒流控制。

1 SP型CPT系统工作原理

对于单级谐振型CPT系统，根据原、副边谐振型的串、并联形式，通常可分为SS、PP、PS、SP型4种电路拓扑。以下以SP型电路拓扑为例，其他拓扑与之类似。SP型结构电路拓扑如图1所示。

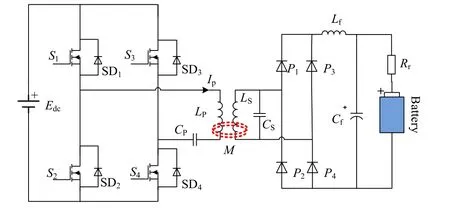
图1 SP型CPT系统电路拓扑

SP型CPT系统可分为原边和副边两部分，都通过高频磁场进行耦合以完成能量的传输。其中原边部分包括直流输入Edc，高频逆变环节(S1～S4)及串联谐振环节(LP,CP)。高频逆变将直流输入转换为高频方波电压输出，而串联谐振环节主要用于将高频方波输入转换为高频正弦谐振电流，并在激磁线圈(LP)周围产生高频磁场。而处于邻近空间中的拾取线圈(LS,LS)将在高频磁场上产生感应电动势，并通过副边的并联谐振环节(LS,CS)产生谐振以提高功率传输能力。高频整流(1P～4P)及滤波环节(Lf,Cf)主要用于将高频形式的能量转换为直流形式输出给充电电池，其中Rr代表电池内阻。

2 系统GSSA模型建立

在直流电压源vdc激励下，原边的全桥逆变电路通过在一个开关周期内交替导通或关断开关管对(S1,S4)和(S2,S3)，使得高频谐振网络工作在正向能量注入和反向能量注入两种模态下，以获得高功率密度的能量发射磁场。因此，CPT无线充电系统的时域微分方程可描述为：

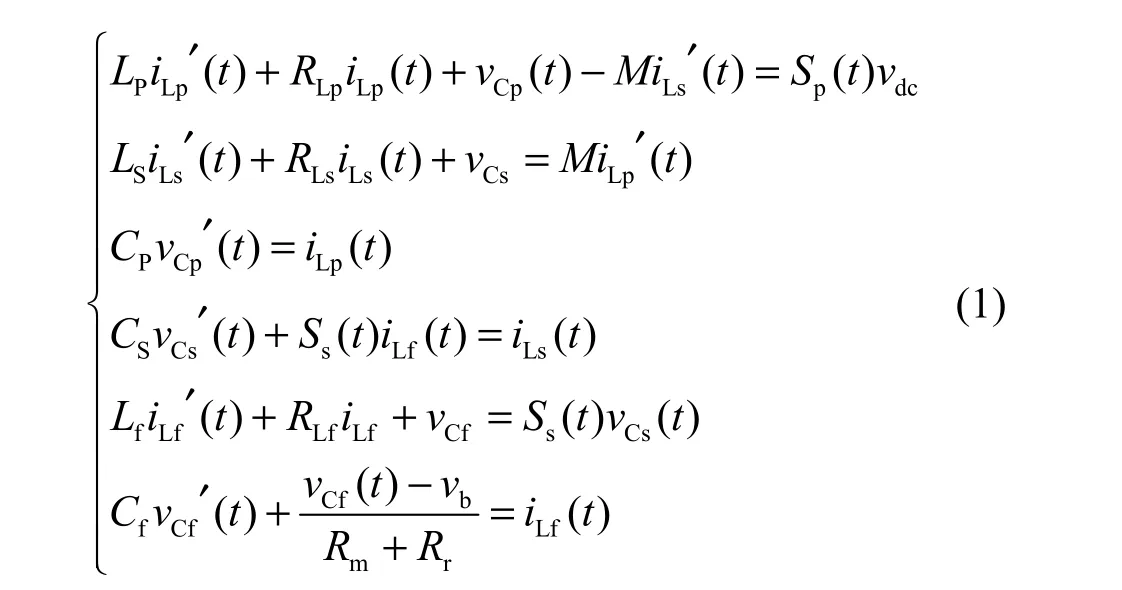
式中，RLp、RLs、RLf分别表示电感LP、LS、Lf的内阻；Rm是一个与电池串联的测量电阻，用于测量充电电流的大小；Sp(t)、Ss(t)分别代表原边逆变环节及副边整流环节的开关非线性函数，可定义为二值逻辑形式：

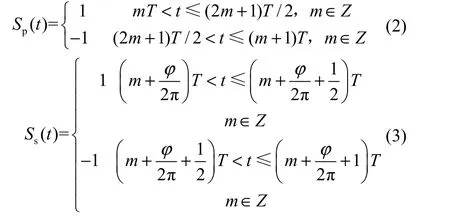
式中，ϕ为原、副边开关非线性函数的相角差，函数逻辑值为1时代表开关管导通，为−1时则代表对应的开关管关断。

对式(1)中的电路变量按傅里叶级数展开，其中直流变量的奇次谐波分量和交流变量的偶次谐波分量都近似为零。当系统工作在固有谐振频率点附近时，交流变量具有准正弦波振荡特性，采用一次谐波分量即可较好的近似，而对于经过滤波后的直流变量，由于纹波较小，采用零次谐波分量也可以较好的近似。因此，各电路变量的傅里叶展开形式可近似表示为：

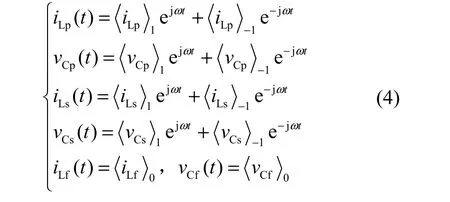
由于交流变量经傅里叶级数展开后，其奇次谐波分量共轭对称：

根据傅里叶系数的微分特性，式(1)可转化为以各阶谐波分量为系统变量的频域微分方程形式：

3 H∞控制器设计

为实现原边主动控制，系统控制原理采取根据副边输出充电电流幅值，通过控制器计算出所需的原边直流输入电压，实现对输出充电电流的控制。对于CPT充电系统而言，为保证恒流充电模式下充电电流具有较小的变化、有界的充电电压及直流输入电压，模型中选择充电电流io、充电电压vo及输入电压vin作为系统的被调输出，并依次附加性能加权函数Wo、Wd、Wu，组成系统的被控向量在充电过程中，由于电池电压的变化会影响其充电电流，因此，把电池电压当作系统的扰动输入，如图2所示。

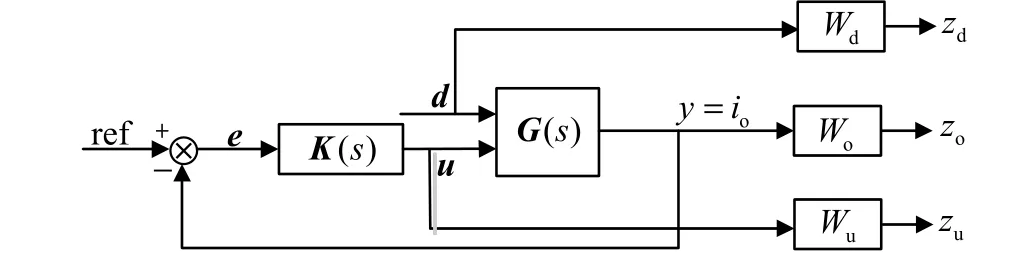
图2 闭环控制系统框图

其中，性能加权函数Wo和Wu分别反映被控系统高频未建模部分和中低频参数不确定性的范数有界性，性能加权函数Wd则表示恒流干扰的频谱特性。

在加权函数下系统增广对象模型可以表示成状态空间方程形式：

从效果来看，新生活运动并未取得蒋介石期望的成效，反而迅速沦为空洞的官样文章。之所以失败，原因是多方面的，单从意识形态建设的角度来看，一是其内容和指向上偏重传统，与现代国家的目标背离;二是意识形态的宣导依赖于党政机关甚至军警的强力推动，而没有政党嵌入式的动员。正如魏斐德指出的，南京国民政府“与欧洲法西斯相比，最显著的差异在于，国民党人无力或者不愿去发动真正的群众运动”⑯。基于上述两点，新生活运动的效果不佳可想而知。

控制器Riccati方程和观测器Riccati方程分别对应着唯一的Hermitian矩阵H和J，定义为：

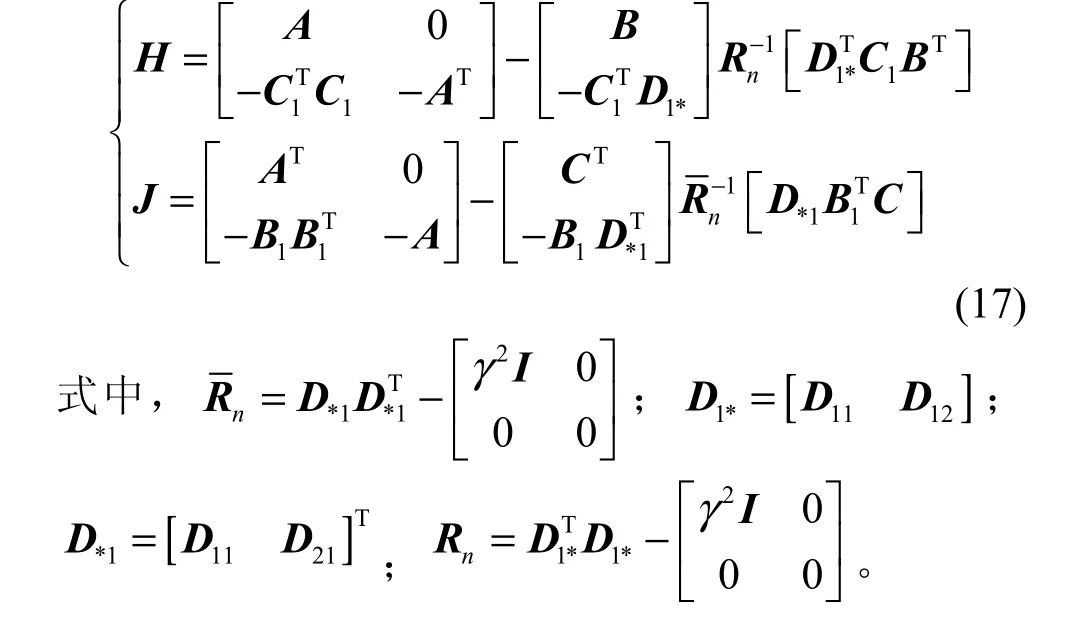
依据上述Hermitian矩阵的特征值分解，即可得出对应Riccati方程的解X和Y。

为获得最优的H∞综合控制器，首先给定γ值的上下界及一个最小偏差δ，并采用γ平分算法，反复迭代求解X和Y，直到γ的上一次值与最后一次值的偏差小于δ。但是对于每一次迭代的γ值，在求解Riccati方程的过程中，都必须检测下述的条件，以保证H∞控制器的存在。

1) 哈密顿矩阵H和J没有位于虚轴的特征值；2) 控制器Riccati方程的解X和观测器Riccati方程的解Y均为半正定矩阵；3)ρ(XY)<γ2， 即两个Riccati方程解的积矩阵的谱半径小于γ2。

基于Riccati方程的解，H∞控制器传函阵为：

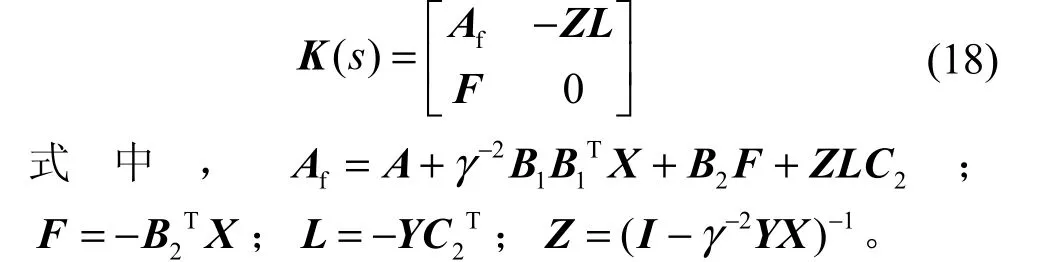
在求解H∞综合控制器时，设γ的边界条件为0<γ≤1，最小偏差为0.001，γ迭代过程从γ=1开始，全部的11次迭代过程参数均符合H∞控制器的存在条件。第11次和第10次迭代时的γ值达到了预设的最小偏差，此时，γ最优值为γopt=0.088。

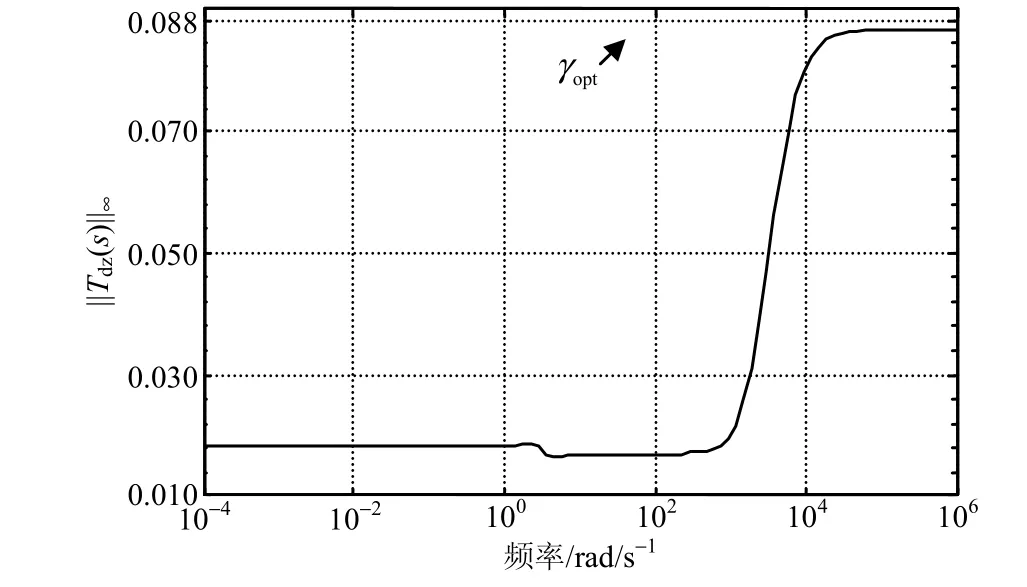
图3 频率响应曲线

4 实验研究

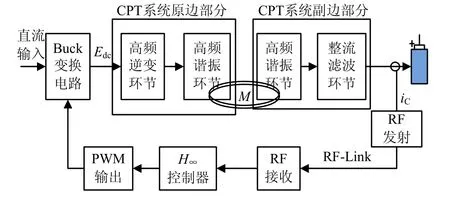
图4 实验系统结构图

实验系统结构与图1所示的CPT系统结构相同，只是在其原边输入端加入一个Buck变换电路以调节CPT系统的直流输入，从而主动控制副边充电电流恒定。充电对象采用锂电池作为充电对象。副边通过检测充电电流，再通过射频模块将电流信息发射至原边，而原边接收后经过H∞控制器后产生控制量，经PWM模块后转换成PWM驱动波形驱动Buck模块产生调节作用。实验系统所采用的参数如表1所示。

表1 实验参数表

为便于DSP程序实现，控制律可通过离散差分方程来表示：

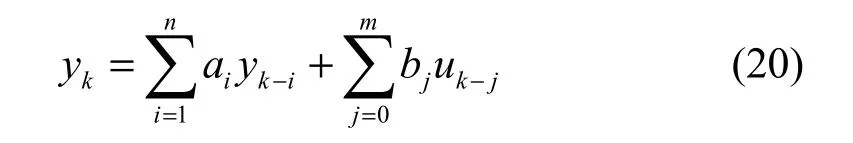
为验证系统在负载扰动条件下的控制性能，设定控制目标为恒定充电电流为4 A。分别测试了充电过程中突加和突减负载的控制效果。在充电过程中，被充电电池突然并入和缷去一个4 Ω的阻性负载，分别对应图5中负载跳变1和2，控制器对输出充电电流的控制效果，如图5所示。

从图中可以看出，在负载跳变点1，即突然并入阻性负载时刻，输出充电电流出现1 A的超调，但在控制作用下，经过15 ms的调节过程即进入系统稳态。稳定后充电电流幅值为4 A。在负载跳变点2，即突然移除并入的阻性负载时刻，输出充电电流同样出现1 A的超调。但在控制作用下，经过12 ms的调节过程进入系统稳态，稳定后充电电流幅值仍保持为4 A。从而验证了在负载振动条件下系统的控制效果。图中下方为原边谐振电流iP的波形，可以看出在控制作用下，原边谐振电流根据负载情况进行相应的调整以适应负载变化。

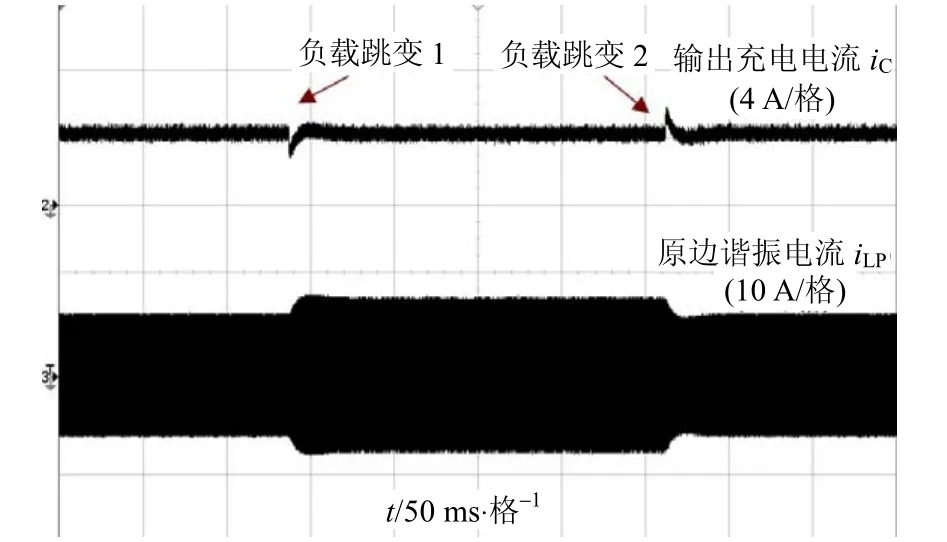
图5 负载跳变实验波形

为验证系统对于控制目标变化的跟踪效果，进行了给定跳变的实验测试。在实验中，设定控制目标分别产生两次跳变，一次是从4 A至1 A，另一次为4 A至1 A，分别观察输出充电电流的跟踪效果。所测得的实验波形如图6所示。

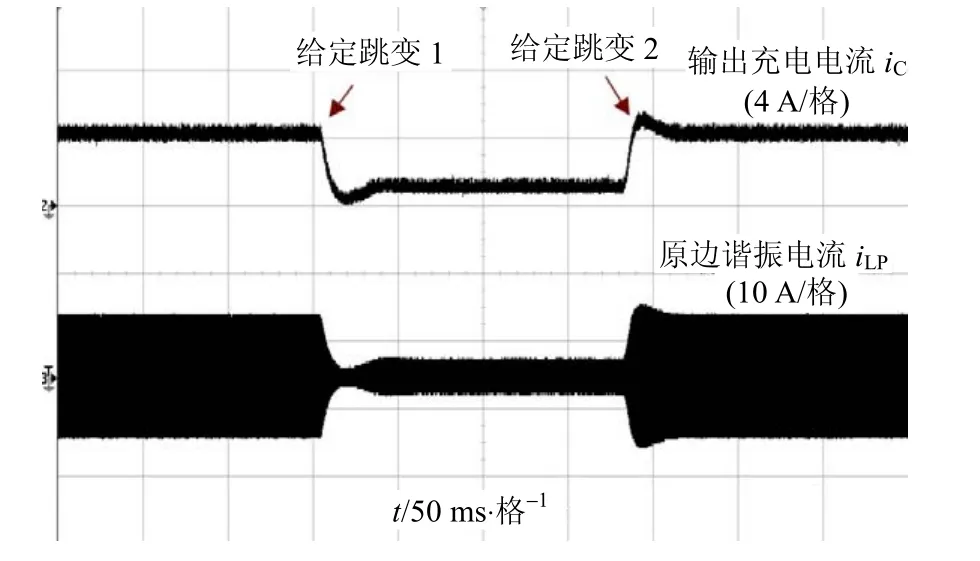
图6 给定跳变实验波形

从图中可以看出，在给定跳变点1，即控制目标由4 A跳至1 A时，输出充电电流经历了一个25 ms的调节过程后进入稳态，并产生了1 A的超调，此时原边谐振电流也相应减小以适应控制目标变化。而在给定跳变点2，即控制目标由1 A跳至4 A时，输出充电电流也经历了一个20 ms的调节过程进入稳态，并产生1 A的超调。

为验证输出充电电流对于给定线性变化的跟踪效果，设定控制目标从1 A至4 A线性变化，验证输出充电电流的跟踪效果。所测得的实验结果如图7所示。

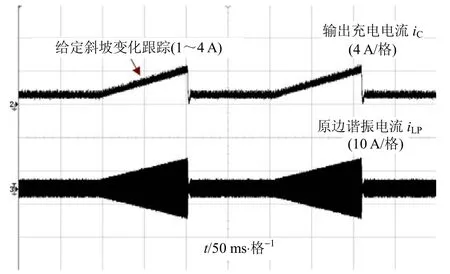
图7 给定斜坡跟踪实验波形

可以看出，在控制目标给定线性变化过程中，输出充电电流始终保持较好的跟踪控制效果，原边谐振电流峰值也从5 A相应变化至13 A以满足控制的需求。从以上分析可以看出，在控制作用下，系统输出电流达到较好的稳恒性及鲁棒性。

5 结 论

围绕非接触电能传输系统的输出恒流充电控制问题，本文提出了一种基于原边主动控制的解决方法。该方法可根据不同的负载条件，动态调节原边直流输入电压，对原边谐振电流产生调节作用以控制能量传输磁场幅值，最终实现对输出充电电流产生控制以保证其稳恒性。该方法对其他类型电力电子系统也具有一定参考价值。

[1] WU Y Z , HU A P, BUDGETT D, et al. Harmonic analysis of voltage-fed full-bridge converter for TET application[C]//5th IEEE Conference on Industrial Electronics and Applications. Taichung, Taiwan, China: IEEE, 2010: 1040-1045.

[2] ZAHEER M, PATEL N, HU A P. Parallel tuned contactless power pickup using saturable core reactor[C]//IEEE International Conference on Sustainable Energy Technologies. Kandy, Srilanka: IEEE, 2010.

[3] WU H H, GILCHRIST A, SEARLY K, et al. A review on inductive charging for electric vehicles[C]//Electric Machines & Drives Conference. Niagara Falls, Canada:[s.n.], 2011: 43-47.

[4] JANG Y T, JOVANOVIC M M. A contactless electrical energy transmission system for portable-telephone battery chargers[J]. IEEE Transactions on Industrial Electronics,2003, 50(3): 520-527.

[5] 戴欣, 孙跃. 感应电能传输系统能量注入控制方法研究[J]. 电子科技大学学报, 2011, 40(1): 69-72.DAI Xin, SUN Yue. Study on energy injection control method for inductiv power transfer system[J]. Journal of University of Eletronics and Technology of China, 2011,40(1): 69-72.

[6] DAI X, HUANG X Y. Study on dynamic accurate modelling and nonlinear phenomena of a push-pull soft switched converter[C]//1st IEEE Conference on Industrial Electronics and Applications. Singapore: IEEE, 2006.

[7] HU A P. Selected resonant converters for IPT power supplies[D]. Auckland: The University of Auckland, 2000.

[8] BOYS J T, COVIC G A, GREEN A W. Stability and control of inductively coupled power transfer systems[J]. IEE Proceedings: Electric Power Applications, 2000, 147(1):37-43.

[9] COVIC G A, BOOYS J T, TAM A M, et al. Self tuning pick-ups for inductive power transfer[C]//PESC 39th IEEE Annual Power Electronics Specialists Conference. Rhodes,Greece: IEEE, 2008: 3489-3494.

[10] HSU J W, HU A P. Determining the variable inductance range for an LCL wireless power pick-up[C]//IEEE Conference on Electron Devices and Solid-State Circuits.Tainan, Taiwan, China: IEEE, 2007: 489-492.

[11] SI P, HU A P, MALPAS S, et. al. A frequency control method for regulating wireless power to implantable devices[J]. IEEE Transactions on Biomedical Circuits and Systems, 2008, 2(1): 22-29.

[12] KUMAR A, HU A P. Linearly tuned wireless power pick-up[C]//IEEE International Conference on Sustainable Energy Technologies. Kandy, Srilanka: IEEE, 2010.

[13] ZAHEER M, PATEL N, HU A P. Parallel tuned contactless power pickup using saturable core reactor[C]// IEEE International Conference on Sustainable Energy Technologies. Kandy, Srilanka: IEEE, 2010.

[14] LI H L, HU A P, COVIC G A, et al. A new primary power regulation method for contactless power transfer[C]//IEEE International Conference on Industrial Technology.Churchill, VIC, Australia: IEEE, 2009.

[15] LI H L, HU A P, COVIC G A. A power flow control method on primary side for a CPT system[C]//International Power Electronics Conference-ECCE Asia. Sapporo, Japan:[s.n.], 2010: 1050-1055.