局部特征在航拍图像拼接中的应用

曹 健，李 侃，高春晓，刘琼昕

(1. 北京工商大学计算机与信息工程学院 北京 海淀区 100048; 2. 北京理工大学计算机学院 北京 海淀区 100081)

航拍图像拼接技术是当前机器视觉领域的一个研究热点，已经被广泛应用于地理信息系统、地质灾害监测、城市规划和战场态势评估等许多方面。其主要目的与一般的图像拼接一样，将一组互相有重叠部分的图像序列进行空间配准，拼成一幅包含各图像序列信息的宽视角、完整的新图像，以满足现实要求[1]。但是，由于是在飞行器上对地面场景的俯视拍摄，所以又有其自身的特点和难点，如飞行器姿态变化导致的航拍视角改变、飞行器升降造成的图像分辨率不同、天气状况对图像质量的影响等。

图像拼接方法通常可以分为两类[2-4]：1) 将场景投影到柱面坐标下进行拼接，该类方法的模型简单且计算速度快，但是要求相机只能围绕光心做水平旋转运动，还需要获取拍摄每幅图像的焦距，比较适合于360°全景图像拼接。2) 以仿射变换模型为理论基础，广泛应用于航拍图像拼接，一般需要根据飞行器和相机的参数计算图像的位置坐标并排列图像，然后检测相邻图像重叠区域内的对应点，以求得图像间的变换关系。航拍图像的特殊性使图像的位置坐标不准确，有时还需要从航拍视频中抽取图像进行拼接，需要一种更为稳健高效的拼接方案。

本文在飞行器和相机具体参数未知的情况下快速拼接航拍图像，不依赖复杂的相机标定设备、旋转台和陀螺仪等；并尽量降低对航拍的限制条件，允许图像之间较大的亮度差异以及相机的轻微晃动等。本文提出基于局部特征的航拍图像拼接算法主要面向一般情况，如使用普通的航拍CCD相机或摄像机，航拍设备位于飞机底部的一个近似固定视点，相邻图像间有不小于16%的重叠，拍摄所有图像时焦距保持不变等。特殊设备拍摄的照片以及在精确参数下的图像拼接不在本文的研究之列。

本文介绍了基于多分辨率技术的图像配准方法，讨论了如何利用放射变换矩阵进行图像变换，阐述图像融合技术。

1 基于多分辨率技术的图像配准

图像配准一般指对取自不同传感器、不同视角或不同时间的两幅或多幅图像进行信息互补的处理过程。在图像拼接领域主要用来确定内容相关的几幅图像中重叠区域的位置以及范围，所以有的文献也称为图像对齐。相对于灰度相关、相位相关等传统方法[5-7]，基于特征的图像配准方法运算速度较快，适用范围较广泛，获得的配准结果相对稳定，逐渐成为当前主流的图像配准方法。

目前已有的基于特征的图像配准方法普遍存在的问题是它们提取的目标特征对噪声较敏感，在灰度变化、形状变化以及遮挡的情况下性能不够稳定，无法满足成像情况相对复杂的航拍图像的需要。近年来，国内外学者提出了一些新的局部特征，并在大量的工程应用中验证了它们的性能相对优越、适用范围较广泛。

局部特征提取包括特征点检测和特征区域描述两部分的内容：Harris-Laplace检测算子、Hessian-Laplace检测算子[8]和DoG (difference of gaussian)检测算子[9]都是目前特征点检测方法中的研究热点；SIFT(scale invariant feature transform) 描述子[10]和GLOH(gradient location orientation histograms)描述子在众多特征区域描述子中应用最广泛，性能也相对稳定。

文献[7-10]都指出，在复杂内容的图像中提取的特征点非常多，过多的特征点不仅会加重计算负担影响效率，而且会对特征匹配造成干扰，不利于航拍图像序列的准实时拼接。本文的拼接方法只需利用少量(3个以上)特征点即可完成图像配准，对特征点的提取质量提出了较高的要求，而多分辨率分析为解决这个问题提供了一条有效的途径。

当观察一幅图像时，通常看到的是相连接的纹理与灰度级相似的区域，它们相互结合形成了物体的视觉表示。如果目标物体的尺寸很小或对比度不高，一般采用较高的分辨率观察；如果物体尺寸很大或对比度很强，则只需较低的分辨率。如果图像中同时存在大小不等的物体，或者强弱不均的对比度，以不同分别率对它们进行研究将在图像模式识别中具有不可替代的优势。

作为解释多分辨率分析概念的一种简单而又有效的结构，图像金字塔最初应用于机器视觉和图像压缩方面，它很直观地展示出了由粗糙到精细的处理策略的魅力所在。一幅图像的金字塔就是一系列以金字塔形状排列的不同分辨率的图像集合，其底部是待处理图像的高分辨率表示，顶部是低分辨率的近似，当向金字塔由底向上移动时，尺寸和分辨率依次降低。

如图1所示，由于从机载摄影器材上获取的图像分辨率较高，本文通过建立图像金字塔来降低待匹配图像的分辨率，在低分辨率的图像序列上提取出更具代表性的特征点对，并计算出这些特征点在原始图像中的位置，从而进行图像变换。

图1 利用多分辨率技术进行图像配准

两幅图像之间的匹配应该满足唯一性、相似性和连续性等3个基本约束条件，即“马尔模型”[11]。一方面，目标表面任意一点到观察点的距离是唯一的，由此推得一幅图像中的一点在另一幅图像中最多只有一个对应点；两幅图像中对应的特征应该有相同的属性，即对应点在某种度量下应当具有相似的特征描述符；因凹凸不平引起的目标表面的深度变化是缓慢的，即视差变化具有连续性。

由于图像的内容千差万别，加上场景中的运动物体、不重叠内容以及图像质量等因素的存在，一幅图像中的局部特征并不一定能在另一幅图像中找到相似的特征，需要采取措施剔除产生干扰的噪声点，通常称为“外点”。许多图像的背景较相似并不具有区分性，如天空、旷野之类，它们的局部特征之间的距离小于有用的特征之间的距离，但是它们并不能描述图像的主要内容，所以设置一个全局性的距离阈值来决定局部特征匹配与否是不合适的。可以通过比较最近邻(first nearest neighbor)特征和次近邻(second nearest neighbor)特征的距离有效地甄别局部特征是否正确匹配，这是最邻近距离比值法(nearest neighbor distance ratio, NNDR)，判断特征匹配的条件[8]为：

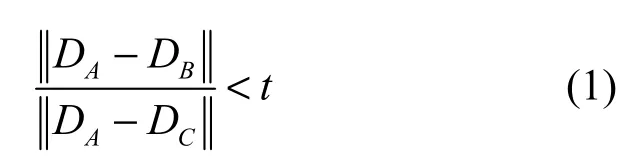
式中，DA为待匹配特征；DB为最邻近特征；DC为次邻近特征。

该方法理论来源是如果一个特征在一幅图像中与两个特征的距离都很相近，那么该特征的区分度较低，也违背了文献[12]提出的“匹配应该满足唯一性”的原则，会对图像相似度的判断产生干扰。

2 图像变换

相邻帧图像之间往往存在着复杂的几何变换关系，要进行图像配准就需要计算相应的变换矩阵。理论上在图像变换的时候考虑的参数越多，得到的结果越精确。但在实际应用中，由于飞行器飞行轨道的起伏、地面物体高度的变化等因素，参数过多的变换矩阵反而起到放大误差的效果，并且需要至少7个特征点对才可以进行配准。

通过对实际数据的研究发现，航拍平台一般距离地面较远，就可以将一定范围内的拍摄场景近似为一个平面区域，进而把一定长度的航拍图像序列变换到同一个成像平面内完成图像配准。仿射变换可以描述图像的旋转、平移和缩放等运动，较符合航拍图像的特点。该方法利用3个以上特征点即可完成图像拼接，不仅极大简化了计算，拼接的最终效果也能够达到相应要求。

设成像平面上某一点Pi的坐标为(xi,yi)，其三维齐次坐标为(xi,yi,1)。设一个观测点在两个相邻帧图像上所成的像点分别为P1和P2，则这两点的齐次坐标之间满足如下关系：

式中，T为8个参数的投影变换矩阵。实验结果显示，由于航拍图像序列中相邻两帧图像之间的视差变化缓慢，可以通过仿射变换矩阵近似表达式(2)中的T，有效地简化了计算，即有：

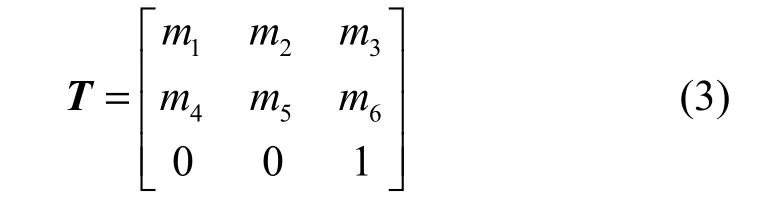
根据线性方程的相关理论，式(3)中6个参数的仿射变换矩阵最少应该通过3对特征点才可以进行求解。而在实际应用中往往检测出不止3对特征点，需要利用最小二乘法来估计T的参数，计算所得的相应误差为：

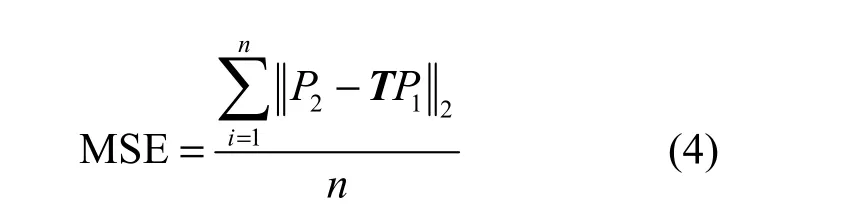
3 图像融合

由于图像采集时拍摄条件往往会发生变化，在图像处理过程中也会引入一些误差，这些因素都会导致初步拼接后的图像中存在视觉上不连续的条带。如何消除这种痕迹，使图像过渡更自然，这正是图像融合技术需要解决的难题。

现有的图像融合算法通常在像素级、特征级和决策级等3个层次进行。目前，像素级融合常用的方法主要有直接平均融合、加权平均融合和多分辨率融合。直接平均融合简单但是通用性较差，如果场景中存在运动目标会产生“鬼影(ghost-like)”现象；多分辨率方法效果好、通用性强，但是计算过于复杂，不适宜大场景的准实时拼接。本文采用了加权平均方法中的渐入渐出融合算法，在保证航拍图像序列准实时拼接的同时，实现了图像内容的平滑过渡。

文献[13]提出了渐入渐出融合算法，设f1和f2是两幅待拼接的图像，将它们按照线性加权的方法进行融合，融合后的图像像素f可表示为：

式中，d1和d2表示与重叠区域的宽度有关的权重值，并且d1+d2= 1 ， 0 ≤d1，d2≤1。假设当前像素的横坐标为xi，重叠区域左右边界的横坐标分别为xl和xr，则在重叠区域中d1由1渐变至0，d2由0渐变至1，即有：

在对单程航拍的图像序列进行拼接时，采用上述方法仅针对相邻两幅图像的x方向上做了平滑过渡，基本可以满足需求。如果图像序列是盘旋拍摄或者沿“几”字型路线拍摄的情况下，需要进一步考虑到多幅图像、各个方向上的平滑。本文借鉴了文献[14-15]的思想和方法，为图像的每个像素分配权重，该权重与像素到图像边缘的距离成正比，即有：

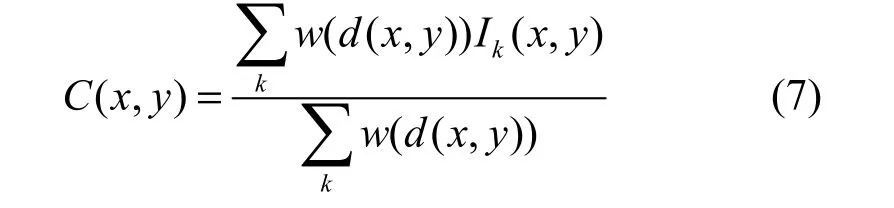
式中，w是单调函数，一般取w(x)=x；Ik(x,y)是第k幅图像在(x,y)点的灰度值；d(x,y)的计算可以简单地取(x,y)点到图像四条边的最小距离。

4 实验结果与分析

为了验证本文方法的有效性，采用VC++ 6.0平台和OpenCV 2.0函数库实现了航拍图像序列自动拼接算法，并且通过大量真实的无人机可见光图像序列和视频对相关算法进行了测试和验证。

4.1 实验参数设置

针对航拍图像场景较大、天气和飞行器姿态的影响普遍存在的情况，本文对多种特征区域检测算法以及描述子进行了实验分析，发现通过DoG检测算子和GLOH描述子提取的局部特征不仅对图像的平移、旋转、缩放变换不敏感，而且对光照变化以及复杂的投影变换也具有很强的适应能力，较适合用于航拍图像序列的处理。

由于局部特征可以看作高维向量空间中的点，可以通过计算两个点之间的接近程度衡量图像特征间的相似度。目前最为常用的相似度度量有直方图相交法、欧式距离、马氏距离、EMD距离等，而相似度度量具有特征依赖性，不同的特征应该应用不同的度量方法才能获得最佳的效果。经过实验对比可以发现，对于SIFT和GLOH等局部特征在图像匹配中的应用，用欧氏距离作为相似度度量可以满足实际应用的要求。

本文采用最邻近距离比值法消除“外点”的影响，实验从图像数据库中选取的待匹配图像，共提取了40 000个GLOH特征，对这些待匹配的图像进行了随机数值的尺度变化和平面旋转，并进行了深度小于30°的视角变化处理，同时也加入2%的高斯噪声。结果表明，当剔除与最近邻点和次近邻点距离比值大于0.8的特征点对时，排除了90%的外点而仅仅误删了5%的正确特征点对。

用穷举法搜寻最邻近点以及次临近点可以得到最精确的结果。但是由于本文所用的特征空间高达128维、航拍图像的特征点数量较多，又有准实时的速度要求，搜索算法的效率成为整个系统的一个瓶颈。所以本文使用了BBF (best-bin-first)算法[10]，设定的约束条件是检查前200个最邻近候选节点，该算法在搜索速度提高了2个数量级的同时，平均丢失5%的特征点对，这对于航拍图像的准实时拼接是可以容忍的。

4.2 拼接效果分析

图2a所示是无人机航拍的一组关于黄河凌汛的照片，图像上主要是自然景物地貌，人造目标较少，这对于计算机自动拼接是一个挑战。本文的拼接方法十分稳健，局部特征提取技术减少了噪声干扰和光照变化的影响，如图2b所示。多分辨率技术的应用也有效地降低了图像配准的计算开销，通过比较最近邻点和次近邻点的距离的方法也可以有效地剔除“外点”。

图2 黄河凌汛的航拍图像拼接结果

图3a所示是无人机在太原火车站上空拍摄的一组照片，图3b所示为其拼接后嵌入Google地图的效果。可以看出，计算机自动拼接后的航拍图像在严格对应于地理信息系统时还存在一些问题。但从一般意义上讲，这部分内容并不属于图像自动拼接技术的研究范畴，可以在下一步工作中引入人机交互的方法，根据相关参数对拼接图像进行几何校正。

图3 太原火车站的航拍图像拼接结果

另外，本文提出的方法也适用于航拍视频图像拼接，如图4所示是从一段空中鸟瞰城市的视频里抽取图像进行准实时拼接的效果，表明本文的方法稳定、可靠，在保证运算速度的同时依然能够取得很好的视觉效果。

图4 航拍视频图像拼接效果

5 结 论

本文提出了一种基于局部特征的航拍图像快速拼接方法。该方法对拍摄的条件要求不高，整个拼接过程是全自动实现的，其针对航拍图像序列的特点，利用局部特征和多分辨率技术实现了高效可靠的特征点匹配；通过仿射变换模型将拼接问题简化为像素点空间坐标变换的过程，达到快速精确的目的；在图像融合时借鉴了渐入渐出算法，实现了色彩和亮度的平滑过渡，消除了拼接痕迹。经过大量不同种类图片的拼接测试，证明该方法的拼接效果令人满意，技术非常实用。由于相机未经标定，图像存在几何变形未纠正等问题有待进一步的解决。

[1] SU M S, WANG L, CHENG K Y. Analysis on multiresolution mosaic images[J]. IEEE Transactions on Image Processing, 2004, 13(7): 952-959.

[2] 魏雪丽, 张桦, 马艳洁, 等. 基于最大互信息的图像拼接优化算法[J]. 光电子·激光, 2009, 20(10): 1399-1402.WEI Xue-li, ZHANG Hua, MA Yan-jie, et al. An optimization algorithm of image mosaic based on maximum mutual information[J]. Journal of Optoelectronics⋅Laser,2009, 20(10): 1399-1402.

[3] 王宇, 王涌天, 刘越. 基于SIFT和小波变换的图像拼接算法[J]. 北京理工大学学报, 2009, 29(5): 423-436.WANG Yu, WANG Yong-tian, LIU Yue. Image stitch algorithm based on SIFT and wavelet transform[J].Transactions of Beijing Institute of Technology, 2009, 29(5):423-436.

[4] BROWN M, LOWE D G. Automatic panoramic image stitching using invariant features[J]. International Journal of Computer Vision, 2007, 74(1): 59-73.

[5] 陈辉, 龙爱群, 彭玉华. 由未标定手持相机拍摄的图片构造全景图[J]. 计算机学报, 2009, 32(2): 328-335.CHEN Hui, LONG Ai-qun, PENG Yu-hua. Building panoramas from photographs taken with an uncalibrated hand-held camera[J]. Chinese Journal of Computers, 2009,32(2): 328-335.

[6] 苏娟, 林行刚, 刘代志. 一种基于结构特征边缘的多传感器图像配准方法[J]. 自动化学报, 2009, 35(3): 251-257.SU Juan, LIN Xing-gang, LIU Dai-zhi. A multi-sensor image registration algorithm based on structure feature edges[J]. Acta Automatica Sinica, 2009, 35(3): 251-257.

[7] MIKOLAJCZYK K, SCHMID C. Scale & affine invariant interest point detectors[J]. International Journal of Computer Vision, 2004, 60(1): 63-86.

[8] LOWE D. Distinctive image features from scale-invariant keypoints[J]. International Journal of Computer Vision,2004, 60(2): 91-110.

[9] ROSTEN E, PORTER R, DRUMMOND T. Faster and better: a machine learning approach to corner detection[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010, 32(1): 105-119.

[10] BORENSTEIN E, ULLMAN S. Combining top-down/bottom-up segmentations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008, 30(12): 2109-2125.

[11] MARR D, POGGIO T. A computational theory of human stereo vision[J]. Proceedings of the Royal Society of London. Series B, 1979, 204(1): 301-320.

[12] SZELISKI R. Video mosaics for virtual environments[J].IEEE Computer Graphics and Applications, 1996, 16(2):22-30.

[13] 曹世翔, 江洁, 张广军, 等. 边缘特征点的多分辨率图像拼接[J]. 计算机研究与发展, 2011, 48(9): 1788-1793.CAO Shi-xiang, JIANG Jie, ZHANG Guang-jun, et al.Multi-scale image mosaic using features from edge[J].Journal of Computer Research and Development, 2011,48(9): 1788-1793.

[14] SHUM H, SZELISKI R. Construction of panoramic mosaics with global and local alignment[J]. International Journal of Computer Vision, 2000, 36(2): 101-130.