一种高精度的近场与远场混合源定位算法

蒋佳佳，段发阶，陈 劲，常宗杰

(精密测试技术及仪器国家重点实验室(天津大学)，天津 300072)

一种高精度的近场与远场混合源定位算法

蒋佳佳，段发阶，陈 劲，常宗杰

(精密测试技术及仪器国家重点实验室(天津大学)，天津 300072)

提出了一种高精度的近场和远场混合信号源定位算法．此算法利用混合源阵列流形的对称性特点，从阵列流形里分离出到达角(direction of arrival，DOA)信息，并实现对所有近场与远场信号源DOA的估计．基于得到的DOA估计值，根据近场与远场源距离参数位于不同区间的特点实现对近场及远场源的分类，以及对近场源距离参数的估计．此算法由于充分利用了数据协方差矩阵的信息，并且基于多项式根值方法形成了一个统一的DOA估计器，所以获得了一个高精度的DOA估计性能，且进一步提高了近场源range参数的估计精度．此外，此算法不需要构造高阶累积量，不需要进行二维搜索，不需要进行参数配对；所有的实现过程仅需一维搜索，计算量小，实现简便．数值及与现有算法的对比实验验证了所提出算法的有效性及优越性．

混合源；到达角(DOA)估计；多项式根值；MUSIC；源定位

信号源定位在智能天线、声呐、雷达、麦克风阵列等方面有着重要的应用[1-2]，国内外学者已对这一课题进行了大量的研究工作．针对远场源定位，许多方法已经被提出，如MUSIC(multiple signal classification)算法[3]、ESPRIT算法[4]、Maximum Likelihood Estimation算法[5]等．由于远场源的位置仅仅由它的DOA参数决定，而近场源的位置由它的DOA和距离参数共同决定，所以远场源定位算法不能直接运用到近场源定位中去．为此，一些近场源定位算法被提出，如基于高阶累积量的近场源定位算法[6]、基于二维MUSIC搜索的近场源定位算法[7]等．然而，上述算法是单独针对远场源或近场源而提出的，在实际应用中，阵列可能同时接收到近场源和远场源的混合信号，如基于声呐阵列的水下声源定位[8]、基于麦克风阵列的声源定位[9]以及在电子对抗领域进行信源的无源定位等．为此，Liang等[8]提出了一种twostage MUSIC(TSMUSIC)算法用于定位混合信号源，但算法需要构造高阶累积量矩阵，计算量大．针对TSMUSIC算法计算量大的缺点，Jin等[9]提出了一种基于二阶累积量(based on the second order statistics，BSOS)的混合源算法，大大阵低了计算量；然而此BSOS算法在进行近场源DOA估计时，只利用了数据协方差矩阵的部分信息，且借助了其他估计方法(其他估计方法会带入额外的估计误差到估计结果中去)，这使得它的近场源DOA估计精度受到了限制，并进一步影响了对近场源距离参数的估计．

针对TSMUSIC算法计算量大的缺点和针对BSOS算法近场源DOA及距离参数估计精度不高的不足，本文提出了一种高精度的近场与远场混合源定位算法．一方面，此算法不是基于高阶累积量，而是基于二阶累积量，且利用了多项式根值方法，因此，它的实现过程仅需很小的计算量；另一方面，它充分利用了数据协方差矩阵的信息，没有求助于其他额外的估计技术且利用多项式根值方法实现所有信号源的DOA估计，所以获得了更高的近场源DOA及距离参数估计性能．此外，此算法不需要进行二维搜索，不需要进行参数配对，实现简便．

1 混合源信号模型

图1 阵列配置Fig.1 Array configuration

不失一般性，假设前M1个信号源为远场信号源，则后M-M1个信号源为近场信号源．将第0个阵元的位置设置为信号相位的参考点，则阵列的输出可表示为

其中

假设在进行信源定位前，已通过AIC(Akaike information criterion)或MDL(minimum description length)算法估计出信源数.

2 混合源DOA参数估计方法

由于传感器阵列关于第0个阵元对称，所以从式(2)可得到

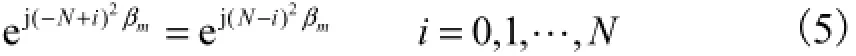
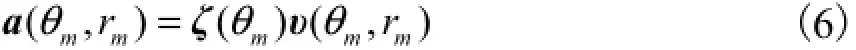
对式(6)进行一般化，也就是对于空间中任意一个近场或远场源而言，其阵列流形向量可表示为

从式(1)可知，()tX的协方差矩阵可表示为

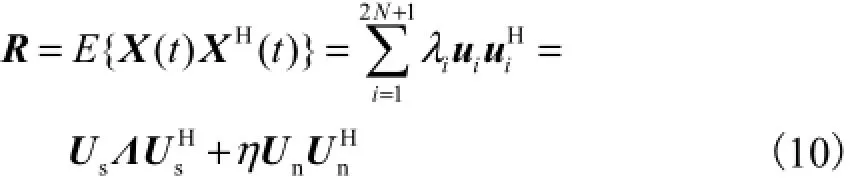
由子空间原理，可得到

进一步，将式(9)代入式(11)可得

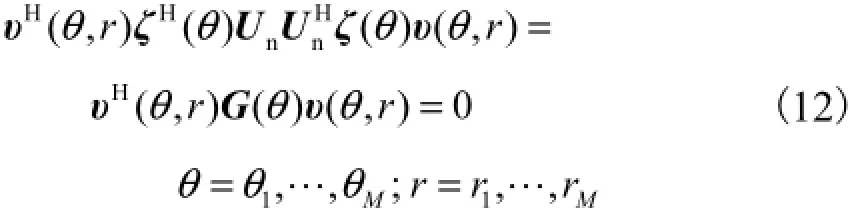
由式(8)可知，不管是近场源还是远场源，H(,)rθ υ都不可能等于零，因此，由式(12)可进一步得到

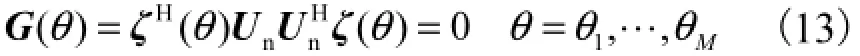
通常情况下，()θG为非负定的共轭对称矩阵，因此，当且仅当()θG为奇异矩阵时，式(12)成立．也就是说，通常情况下，()θG为满秩矩阵[11]，而只有当θ取信号的真实DOA时，矩阵()θG降秩．因此，可利用矩阵()θG的降秩特性来实现DOA的估计为

式中det{}i表示取矩阵的行列式．

从式(14)可知，为了获得所有信号源的DOA估计值，需要进行一维搜索，这将带来较大的计算量．为了降低计算量和提高DOA的估计精度，本文采用多项式根值的方法进一步对式(14)进行处理．

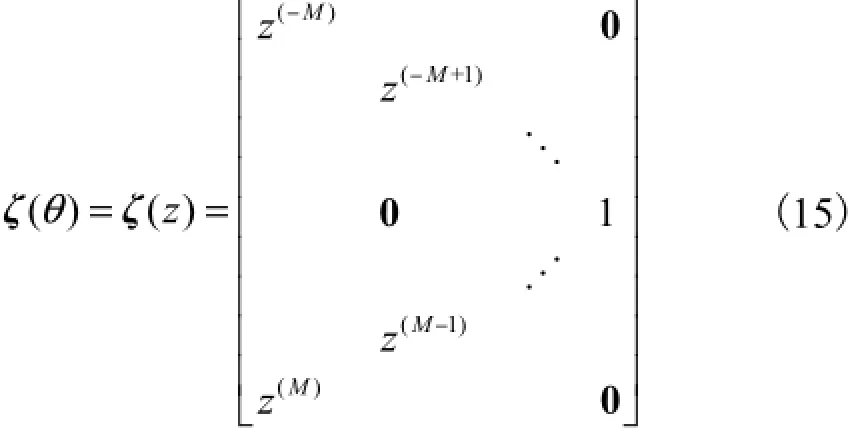
则式(14)的分母可进一步表示为

类似于根值MUSIC算法[12-13]，对()f z求解后能获得M个最接近于单位圆的根值然后利用这M个根，并基于式(17)，能得到所有近场与远场源的DOA估计值，即

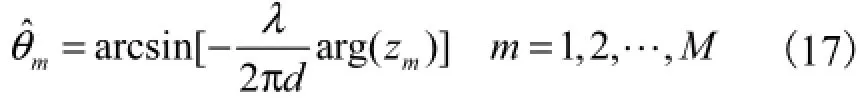
式中arg()i为取相位运算符．

值得注意的是，在实际应用场合中，部分远场源与近场源可能有相同的DOA，所以由式(14)实际得到的谱峰的个数为M′；相对应地，由式(16)实际得到的最接近于单位圆的根值的个数不等于M，而是等于M′．显然，MM′≤，而只有当所有近场源与所有远场源的DOA都不相同时，MM′=才成立．

3 近场与远场源分离及近场源距离参数估计方法

3.1 分离远场源的DOA

利用已求得的噪声子空间获得的MUSIC谱估计式[7]为

值得注意的是，只是通过式(18)来寻找与式(17)估计出来的DOA值相匹配的DOA值，最终的DOA估计值使用式(17)估计出来的结果，而不是式(18)估计出来的结果．这是因为式(17)的估计结果是基于多项式根值方法的，它的估计结果比式(18)的估计结果精度更高．

3.2 识别近场源DOA

在第2节中，本文已估计出所有远场源对应的M1个DOA估计值，而之前通过式(17)有M′个DOA估计值被获得，因此余下的M′-M1个DOA的估计值肯定为近场源的DOA．

然而值得注意的是，近场源DOA的个数应该为M-M1个，而不是M′-M1个，这说明，还有(M-M1)-(M′-M1)=M-M′个近场源与远场源有相同的DOA，这也正是式(17)只获得M′个接近单位圆的根而不是M个接近单位圆的根的原因．

接下来，只要找出剩下的M-M′个与远场源有相同DOA的近场源，就获得了所有近场源的DOA．由于所有远场源的DOA已经得到，且近场源的距离参数r∈[0.6，因此将每个远场源的DOA代入式(18)，并在2D2/λ)内进行一维搜索，就能获得M-M′个谱峰，与这M-M′个谱峰相匹配的DOA即为余下近场源(与远场源有相同DOA的近场源)的DOA；与此同时，通过此一维搜索，也同时获得了M-M′个近场源的距离参数r的估计值．

与第3.1节中一样，只是通过式(18)来寻找与式(17)估计出来的DOA值相匹配的DOA值，最终的DOA估计值使用式(17)估计出来的结果，而不是式(18)估计出来的结果．

3.3 近场源距离参数估计

在第3.2节中已估计出M-M′个近场源的距离参数，在此将对余下的M′-M1个近场源的距离参数r进行估计．

由于在第3.2节中已获得所有近场源DOA的估计值，所以将这些DOA估计值代入式(18)中，并在的区间内进行一维搜索，就能获得M′-M1个谱峰，这M′-M1个谱峰所对应的距离参数即为M′-M1个近场源所对应的range参数估计值．

4 算法优缺点

4.1 阵列孔径

由于ζ(θm)是一个(2N+1)×(N+1)维矩阵，根据子空间原理及式(13)可知，基于一个具有21N+个阵元的均匀线阵，本文中所提出的算法最多能定位N个信号源．而BSOS算法凭借一个具有21N+个阵元的均匀线阵也只能最多定位N个信号源[9]．这说明本文提出的算法与BSOS算法具有相同的阵列孔径．

4.2 DOA估计精度

本文算法首先充分地利用了数据协方差矩阵R的全部信息来形成一个统一的估计器，然后将多项式根值方法引入到DOA的估计中，实现了近场与远场源DOA的联合估计．而BSOS算法首先利用数据协方差矩阵R的信息估计出远场源的DOA，然后再利用数据协方差矩阵R的部分信息去估计近场源的DOA，且在估计近场源的DOA时，借助了斜投影技术[14]．一方面，BSOS算法没有充分利用数据协方差矩阵R的全部信息去估计近场源的DOA；另一方面，斜投影技术[14]将会带来额外的估计误差，从而进一步影响近场源DOA的估计精度．因此，从这两点上来看，本文算法比BSOS算法应有更好的近场DOA估计性能．此外，本文算法在进行DOA估计时，引入计算量更小、估计性能更好的多项式根值方法(参看文献[12]的分析及结论)，所以基于以上3方面，不管是近场源还是远场源，本文算法都应该比BSOS算法具有更好的DOA估计精度．

4.3 近场源距离估计精度

不管是本文算法还是BSOS算法，在进行距离参数估计时，都是基于已被估计出来的DOA值进行的，因此，被估计的DOA值的精度将直接影响距离参数的估计表现．而从上面的分析可知，本文算法比BSOS算法具有更好的DOA估计精度．因此，本文算法应比BSOS算法具有更好的距离参数估计性能.

4.4 计算复杂度

文献[8-9]中仅仅考虑主要的计算量，例如数据协方差矩阵的构造、矩阵的特征分解、MUSIC谱搜索、根值多项式构造．定义DOA参数的搜索间隔为Δθ，距离参数的搜索间隔为Δr．BSOS算法的主要计算过程为:形成一个(2N+1)×(2N+1)和一个(2N+2-T)×(2N+2-T)的矩阵并对这两个矩阵进行特征分解，进行一维MUSIC搜索两次来估计DOA参数，进行一维MUSIC搜索M-M1次来估计近场源的距离参数，其中T表示重叠子向量的个数(参见文献[9]中的式(18))．因此，当假设T=N时，BSOS算法的主要计算复杂度可表示为O{(2N+1)2L+(N+2)2L +式中L为快拍数．

本文算法的主要计算过程为:形成一个(2N+1)× (2N+1)的矩阵，构造根值多项式一次来估计DOA参数，通过一维MUSIC搜索M1次来估计部分近场源(与远场源有相同DOA的近场源)的距离参数，通过一维MUSIC搜索M′-M1次来估计部分近场源(与远场源有不同DOA的近场源)的距离参数．因此，本文算法的主要计算复杂度为

针对非均匀线阵．从文献[9]中的式(17)可以看出，当阵列为非均匀的线阵时，文献[9]中的BSOS算法将无法获得只包含DOA信息的向量y，所以BSOS算法针对非均匀线阵将失效．本文中所提出的算法由于采用求根方法估计信源的DOA，所以也不能用于非均匀线阵中．

5 数值实验

通过计算机数值实验验证该方法的有效性．所考虑的均匀线性阵列由11个阵元(5M=)组成，阵元间距设为/4λ[8-9]．每次的估计值取300次Monte-Carl实验的均值[15]，均方根误差(RMSE)[16]被用作评价各项参数估计性能的准则．为了比较，本文同时给出BSOS算法[9]的仿真结果及Cramer-Rao Lower Bound(CRLB)[8-9]．

实验1主要测试本文算法在混合源(近场源与远场源无相同的DOA)时的性能．假设空间中存在一个近场源和一个远场源，且它们的DOA不相同．近场源的位置为远场源的位置为首先，假设快拍数固定为150，信噪比SNR从0,dB到30,dB不断变化，DOA和距离参数估计的仿真结果如图2和图3所示．然后，假设信噪比固定为10,dB，快拍数从50到2,000不断变化，DOA和距离参数估计的仿真结果如图4和图5所示.

从图2可知，本文算法比BSOS算法具有更高的近场DOA估计精度，这是因为本文算法充分利用了数据协方差矩阵R的全部信息，没有求助于其他额外的估计方法，并且结合了估计性能更好的多项式根值方法．另外，本文算法比BSOS算法具有更好的远场DOA估计性能，这是因为本文算法结合了估计性能更好的多项式根值方法．从图3可知，本文算法与BSOS算法相比，获得了更好的距离参数估计表现．这是因为，本文算法是利用更高精度的DOA估计值去估计距离参数的．图4和图5显示，随着快拍数的变化，本文算法仍然比BSOS算法具有更好的DOA和距离参数估计表现．

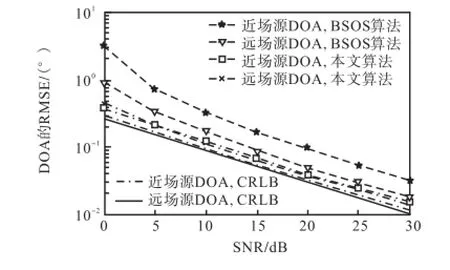
图2 DOA估计性能随SNR变化曲线(混合源且DOA不同)Fig.2RMSE of DOA estimates versus SNR(mixed source with different DOAs)

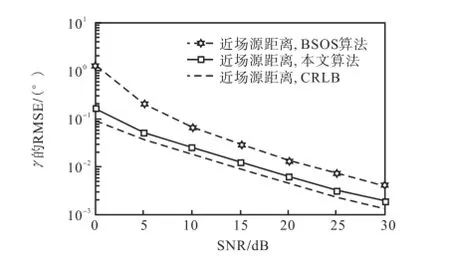
图3 距离估计性能随SNR变化曲线(混合源且DOA不同)Fig.3RMSE of range estimates versus SNR(mixed source with different DOAs)

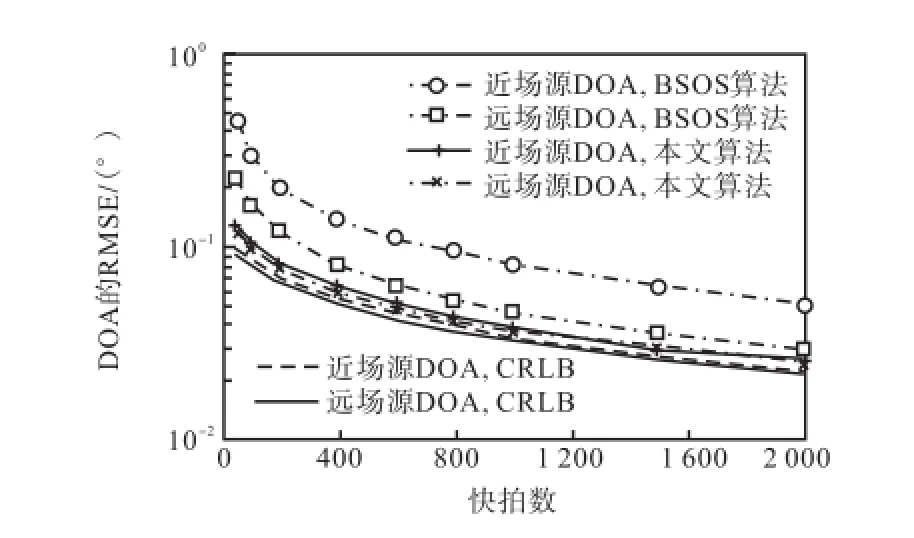
图4 DOA估计性能随快拍数变化曲线(混合源且DOA不同)Fig.4RMSE of DOA estimates versus snapshots(mixed source with different DOAs)

图5 距离估计性能随快拍数变化曲线(混合源且DOA不同)Fig.5 RMSE of range estimates versus snapshots(mixed source with different DOAs)

实验2主要测试本文算法在混合源(近场源与远场源有相同的DOA)时的性能．本次实验中假设有两个信号源分别处在阵列的近场与远场区域中，且它们有相同的D O A．进一步，近场源的位置为2}r=+∞．快拍数为200，信噪比从0,dB到30,dB不断变化，DOA和距离参数估计的仿真结果如图6和图7所示．

由于BSOS算法构造了两个不同的DOA估计器(一个远场估计器和一个近场估计器)来分别实现远场源与近场源DOA的估计，所以即使近场源与远场源有相同的DOA时，BSOS算法都会分别获得近场源与远场源的DOA估计值．而本文算法由于只利用式(17)估计出来的DOA值，所以当近场源与远场源有相同的DOA，只获得一个统一的DOA估计值，图6给出了估计结果．从图6和图7可看出，当近场源与远场源有相同的DOA时，本文算法仍然比BSOS算法具有更高的DOA和距离参数估计精度．远场源的位置为

图6 DOA估计性能随SNR变化曲线(混合源且DOA相同)Fig.6 RMSE of DOA estimates versus SNR(mixed source with the same DOA)

图7 距离估计性能随SNR变化曲线(混合源且DOA相同)Fig.7 RMSE of range estimates versus SNR(mixed source with the same DOAs)

实验3主要测试本文算法在纯近场源时的性能．假设有两个信号源都处在阵列的近场区域，其位置分别为快拍数取为300．DOA和距离参数估计的仿真结果如图8和图9所示．

由图8和图9可以看出，由于BSOS算法只利用数据协方差矩阵R的部分信号来估计近场信号源的DOA，所以当信号源为纯近场源时，本文算法比BSOS算法的优势更大．

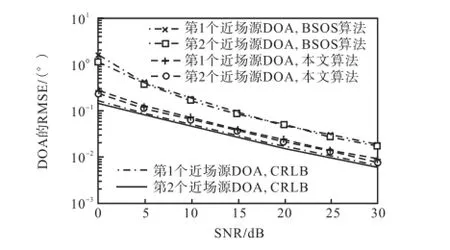
图8 DOA估计性能随SNR变化曲线(纯近场源)Fig.8RMSE of DOA estimates versus SNR(pure nearfield sources)

图9 距离估计性能随SNR变化曲线(纯近场源)Fig.9RMSE of range estimates versus SNR(pure nearfield sources)

实验4主要测试本文算法在纯远场源时的性能．假设有两个信号源处在阵列的远场区域，其DOA分别为快拍数取为500. DOA参数估计的仿真结果如图10所示．

当信号源为纯远场源时，本文算法的优势在于利用了多项式根值MUSIC算法，因此，本文算法获得了更好的DOA估计表现，如图10所示．

图10 DOA估计性能随SNR变化曲线(纯远场源)Fig.10 RMSE of DOA estimates versus SNR(pure far-field sources)

实验5进行算法计算复杂度比较．同样假设阵列由11个阵列组成．首先，根据文献[10]，能获得近场区域的大小；为了实际仿真，假设+∞≜102λ，并且令DOA搜索间隔为Δθ=0.1o、距离搜索间隔为Δr=0.1λ、BSOS算法的重叠子向量的个数T=N[9].假设空间中存在2个远场源和2个近场源，且其中一个远场源的DOA与其中一个近场源的DOA相同．随着快拍数的变化，BSOS算法和本文算法的计算复杂度如图11所示．

从图11可知，当快拍数较小时，本文算法与BSOS算法的计算量相当；当快拍数较大时，本文算法的计算量比BSOS算法更小．

图11 计算复杂度比较Fig.11 Comparisons of computational complexity

实验6进行阵列孔径验证．假设有5个信号源都处在由11个阵元组成的远场区域，其DOA分别为．快拍数取为300，信噪比设为5,dB．本文中算法的空间谱仿真结果如图12所示．从图12中可知，具有11个阵元的线阵能同时成功地定位5个信号源，这说明本文中算法相对于BSOS算法没有阵列孔径损失．

图12 信号源到达角Fig.12 DOA of sources

6 结 语

本文提出了一种高精度的近场与远场混合信号源定位算法．此算法充分利用了数据协方差矩阵的信号，没有求助于任何其他额外的估计方法，且利用了多项式根值方法的优点，因此获得了较高的DOA和距离参数估计表现．此外，本文算法只基于二阶累积量，而不是高阶累积量，且在进行近场与远场DOA的联合估计时，不需要进行一维搜索，因此获得了较低的计算复杂度．此外，本文算法与BSOS算法一样，还具有不需要进行参数配对的优点．从数值实验的结果可以看出，当信噪比较低、快拍数较小时，本文算法仍能获得较高的参数估计精度，这说明本文算法可以被运用在噪声较大且实时性要求较高的场合.

［1］ Krim H，Viberg M. Two decades of array signal processing research:The parametric approach[J]. IEEE Signal Processing Magazine，1996，13(4):67-94.

［2］ Johnson D H，Dudgeon D E. Array Signal Processing—Concepts and Techniques[M]. Englewood:Prentice-Hall，1993.

［3］ Schmidt R O. Multiple emitter location and signal parameters estimation[J]. IEEE Transactions on Antennas and Propagation，1986，34(3):267-280.

［4］ Zhang X，Xu D. Low-complexity ESPRIT-based DOA estimation for colocated MIMO radar using reduceddimension transformation[J]. Electronics Letters，2011，47(4):283-284.

［5］ Aubry A，de Maio A，Pallotta L，et al. Maximum likelihood estimation of a structured covariance matrix with a condition number constraint[J]. IEEE Transactions on Signal Processing，2012，60(6):3004-3021.

［6］ Norman Y，Benjamin F. Performance analysis of high-order ESPRIT for localization of near-field sources[J]. IEEE Transactions on Signal Processing，1998，46(3):709-719.

［7］ Huang Y D，Barkat M. Near-field multiple source localization by passive sensor array[J]. IEEE Transactions on Antennas and Propagation，1991，39(7):968-975.

［8］ Liang J，Liu D. Passive localization of mixed near-field and far-field sources using two-stage MUSIC algorithm[J]. IEEE Transactions on Signal Processing，2010，58(1):108-120.

［9］ Jin H，Swamy M N S，Ahmad M O. Efficient application of MUSIC algorithm under the coexistence of farfield and near-field sources[J]. IEEE Transactions on Signal Processing，2012，60(4):2066-2070.

［10］ Johnson R C. Antenna Engineering Handbook[M]. 3rd ed. New York:McGraw-Hill，2004.

［11］ Pesavento M，Gershman A B，Wong K M. Direction finding in partly calibrated sensor arrays composed of multiple subarrays[J]. IEEE Transactions on Signal Processing，2002，50(9):2103-2115.

［12］ Barabell A J. Improving the resolution performance of eigenstructure-based direction-finding algorithms[C] //In Proceeding ICASSP. Boston，MA，USA，1983:336-339.

［13］ Rao B D，Hari K V S. Performance analysis of root-MUSIC[J]. IEEE Transactions on Acoustics，Speech，Signal Processing，1989，37(12):1939-1949.

［14］ Behrens R T，Scharf L L. Signal processing applications of oblique projection operators[J]. IEEE Transactions on Signal Processing，1994，42(6):1413-1424.

［15］ 段发阶，叶德超，龙 成. 基于 PLL载频跟踪的电容式叶尖间隙测量技术[J]. 天津大学学报，2011，44(4):283-286.

Duan Fajie，Ye Dechao，Long Cheng. Technique for capacitance-type blade tip clearance measurement based on PLL carrier frequency tracking[J]. Journal of Tianjin University，2011，44(4):283-286(in Chinese).

［16］ 欧阳涛，段发阶，李孟麟，等. 恒速下旋转叶片同步振动辨识方法[J]. 天津大学学报，2011，44(8): 742-746.

Ouyang Tao，Duan Fajie，Li Menglin，et al. Method for identifying rotating blade synchronous vibration at constant speed[J]. Journal of Tianjin University，2011，44(8):742-746(in Chinese)．

A High-Accuracy Localization Algorithm for Mixed Near- and Far-Field Sources

Jiang Jiajia，Duan Fajie，Chen Jin，Chang Zongjie
(State Key Laboratory of Precision Measuring Technology and Instruments，Tianjin University，Tianjin 300072，China)

A high-accuracy localization algorithm for the mixed near and far-field sources was proposed in this paper. Making the most of the symmetry of array steering vector，the proposed algorithm first separates the DOA information from the array steering vector so as to finish the DOA estimation of all near- and far-field sources. Then，based on the estimated DOAs，the near-field sources and far-field sources were distinguished from the mixed sources according to the different range intervals of the near-field sources and far-field sources，and the range parameters of the near-field sources were estimated. Because the proposed algorithm，which is based on the polynomial rooting method，makes full use of the data covariance matrix information to form a united DOA estimator for the near-field and far-field sources，it can obtain high estimation performance for both the DOA and range parameters. Besides，the proposed algorithm requires neither high-order statistics nor two-dimensional search(only one-dimensional search). It requires no pairing parameters，either. Therefore，the proposed algorithm only requires low computational cost. Numerical experiment and comparison with other existing algorithms verify the effectiveness and superior performance of the algorithm proposed in this paper.

mixed source；direction of arrival(DOA)estimation；polynomial root value；MUSIC；source localization

TN911.7

A

0493-2137(2013)12-1114-08

DOI 10.11784/tdxb20131210

2012-08-29；

2013-06-03.

国家自然科学基金资助项目(51275349，50375110)；天津市科技支撑计划重点项目(11ZCKFGX03600)；天津市科技兴海专项基金资助项目(KX2010-0006).

蒋佳佳（1986— ），男，博士研究生，tmjiangjiajia@163.com.

段发阶，fjduan@tju.edu.cn.