钢框架-剪力墙模型结构振动台试验与损伤分析

徐龙河，单 旭，吕 杨，李忠献

(1. 北京交通大学土木建筑工程学院，北京 100044；2. 天津大学建筑工程学院，天津 300072)

钢框架-剪力墙模型结构振动台试验与损伤分析

徐龙河1，单 旭1，吕 杨2，李忠献2

(1. 北京交通大学土木建筑工程学院，北京 100044；2. 天津大学建筑工程学院，天津 300072)

对一个1∶4缩尺的3层钢框架-剪力墙模型结构进行振动台试验研究，分析了该结构在强震作用下的动力特性、动力响应及损伤的演化规律．结果表明，随着地震强度增大，结构前两阶自振频率以及层动力放大系数逐渐减小，结构位移反应增大．提出了基于构件层次的损伤模型，该模型考虑了大变形幅值对累积耗能的影响．用该损伤准则对模型薄弱层钢柱的损伤演化规律进行分析，结合IDA分析的结果以及试验结果，对模型的合理性进行了验证.

钢框架；振动台试验；损伤模型；损伤演化

20世纪70年代以来，随着国内外很多结构在地震中发生倒塌破坏，人们对钢结构及钢筋混凝土结构强震下的损伤演化及抗震性能研究的重视程度日渐提高[1-6]．结构模拟地震振动台试验在结构抗震性能研究中具有很重要的作用，试验可以较真实地模拟结构在地震作用下的破坏过程、破坏机理、薄弱环节等进而对结构设计提出改进的建议，同时模拟地震振动台试验也是验证数值模拟有效性的重要手段．

本文对一个3层钢框架-剪力墙混合结构模型进行了地震模拟振动台试验，分别从结构的动力特性、加速度反应、位移反应及损伤演化等几个方面对钢框架部分在强震作用下的失效破坏规律进行了分析．

1 试验概况

试验模型为1∶4缩尺的3层钢框架-混凝土混合结构，平面尺寸为1.2,m×1.555,m，底层层高0.90,m，第2层和第3层层高0.75,m，总高2.4,m．剪力墙截面尺寸均为0.08,m×0.31,m，每层开洞，底层洞口大小为0.78,m×0.15,m，第2层和第3层洞口大小为0.63,m×0.15,m，即连梁高度均为0.12,m，净跨度0.15,m，剪力墙各墙肢纵向4角配置4Φ8钢筋，连梁4角纵向为4Φ8钢筋，中部配置2Φ4钢筋，箍筋均为直径为4,mm的铁丝，混凝土保护层厚度为10,mm．钢框架跨度为1.245,m，钢柱都采用热轧H型钢，钢材为Q235钢，各层钢柱截面相同，尺寸为HW100×100×6×8．框架梁和连梁均采用10号槽钢，截面尺寸为100×48×5.3×8.5．钢梁与混凝土剪力墙采用预埋焊钉铰接连接，钢梁与钢柱采用刚性连接．结构每层的附加质量钢框架部分为640,kg，剪力墙部分为480,kg．试验过程中对结构各层层间位移采用拉线式位移计测量，±5,mm规格的拉线式位移计工作频率范围为0～100,Hz，±250,mm规格的拉线式位移计工作频率范围为0～50,Hz．结构各层加速度采用YJ9A型压电加速度传感器测量，使用频率范围为1,Hz～10,kHz，基座绝缘，适合通用的振动和冲击测量，并在结构钢柱脚、钢梁刚接端、各层混凝土剪力墙墙肢端部布置应变片测量结构关键部位的应变时程，试验测点具体布置及试验结构模型如图1和图2所示．

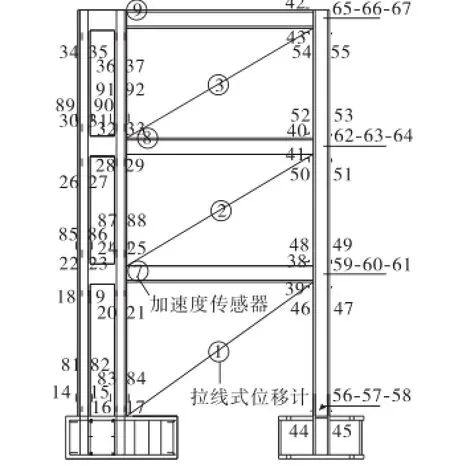
图1 测点布置Fig.1 Layout of test points

图2 试验结构模型Fig.2 Structural test model

沿剪力墙平面内依次输入Tianjin波、El Centro波和Taft波，按1∶3时间缩放，试验分两个阶段进行:第1阶段，研究小震作用下结构损伤对钢框架结构动力特性的影响，将峰值加速度调幅为0.1g、0.2g和0.3g，试验时应避免试件发生大的开裂等破坏；第2阶段，研究强震作用下结构损伤对钢框架结构动力特性的影响及钢框架结构的失效破坏规律，将峰值加速度幅值依次增大，直到试验模型倒塌破坏或达到振动台容许的峰值加速度．

2 试验结果分析

2.1 动力特性

图3 不同工况下白噪声扫描模型的传递函数Fig.3 Transfer function of the model structure under white noise scanning under different test conditions

试验之前及各工况地震波输入之后，对模型结构进行白噪声扫频，记录结构各层加速度反应值，对顶层加速度反应值进行频谱分析，获得模型相对于台面的传递函数，得到不同强度地震作用下结构的自振频率变化规律．图3所示为震前、0.5g时和1.8g地震输入结束时白噪声扫频得到结构顶点位移的传递函数.表1为初始结构和各峰值加速度地震动作用后，结构前两阶自振频率．随着地震强度的增大，结构前两阶自振频率均逐渐减小，与初始结构相比，试验结束时结构基频减小了17.84%，第2阶频率减小了16.2%．

表1 模型结构自振频率Tab.1 Natural frequencies of the model structure Hz

2.2 加速度反应

定义顶层加速度反应峰值与振动台面加速度峰值之比为结构加速度动力放大系数．图4给出了结构顶层加速度动力放大系数随试验工况的变化趋势，可以看出，在3种地震波作用下，模型结构的动力放大系数均随地震动输入幅值的增加而减小，这是由于随着地震强度的增加，结构的塑性程度变大，阻尼增大，刚度降低，损伤加剧所至．

图4 结构顶层加速度动力放大系数Fig.4 Dynamic amplification factor of acceleration at the top story

2.3 位移反应

试验得到结构模型在不同地震波输入下各层的最大层间位移角如表2所示．

图5给出了结构各层最大位移反应包络图，不同地震频谱成分的地震动激励下结构动力响应存在很大的差异．Tianjin波作用下结构位移反应最大，El Centro波作用下结构的位移反应最小，结构首层层间位移角最大，在分别输入PGA为1.8g的Tianjin波、El Centro波和Taft波时，结构首层的最大层间位移角分别为1/53、1/65和1/59．在3种不同强度的地震波作用下，结构各层最大位移反应包络曲线由开始近似直线逐渐变化为曲线，曲线的曲率逐渐增大，这是由于随着输入地震波强度的增大，结构各层的强度和损伤发展出现较明显的差异，结构下部楼层响应增大得更快，强度退化及损伤更严重，首层柱子进入了更强的非线性响应．

表2 结构各层最大层间位移角Tab.2 The maximal story drift angle of each floor 10-3

2.4 损伤分析

对该钢框架-剪力墙混合结构模型进行增量动力分析(incremental dynamic analysis，IDA)，通过IDA曲线上的几个关键点，包括可继续使用(immediate occupancy，IO)点、不倒塌极限状态(collapse prevention，CP)点、整体失稳(global instability，GI)点等，来评价结构在不同水准地震作用下的抗震性能[7]．

图6给出了结构在不同强度的Taft波、El Centro波及Tianjin波作用下的IDA曲线．根据FEMA273[8]的规定，将曲线斜率首次小于0.2Ke(Ke为初始斜率)或曲线上θmax=10%的点定义为结构不倒塌极限状态点(CP点)，通过计算CP点来衡量结构是否倒塌．表3给出了结构模型的IDA曲线上CP点的计算结果，其中Kmin为IDA曲线的最小斜率．可以看出，对于3种不同地震波的IDA曲线，Kmin都大于各自对应的0.2Ke值，这说明在整个试验过程中，结构整体的损伤状态没有达到倒塌．3条IDA曲线在试验结束时的发展走势是呈上升且斜率增大的趋势，这也可以说明结构还没有到达倒塌破坏状态．由于振动台容许峰值加速度及位移存在限值，试验时加载的地震波最大峰值加速度只能加到1.8g．

图5 结构各层最大位移反应包络图Fig.5 Envelope diagram of the maximal displacement of each floor

图6 结构的IDA曲线Fig.6 IDA curves of the structure

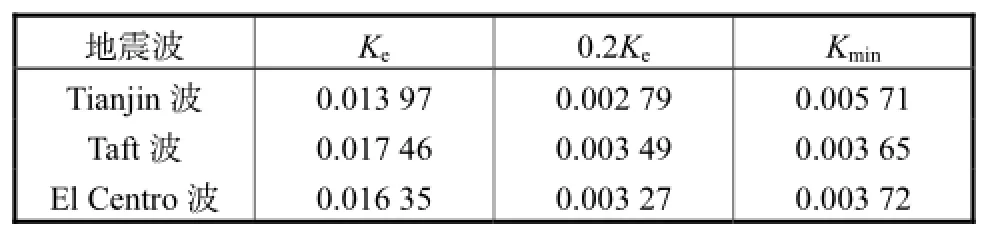
表3 CP点的计算结果Tab.3 Results of the CP point

建筑结构在强震作用下发生破坏甚至连续性倒塌，是竖向承重构件由于损伤累积而逐步丧失继续承载结构自身重力荷载的能力而导致的，即结构损伤过程是柱子竖向承载力逐步丧失的过程．本文提出基于构件层次的损伤模型，该损伤模型是时间的函数并且考虑了大变形幅值对累积耗能的影响，其表达式为

式中:Dj为构件j的损伤指标；为震动开始至t时刻构件j经历的最大位移；参数m=1.3+ 3.5,n0[9](其中n0为轴压比，当n0＜0.2时取0.2)；β为影响参数；δuj为构件j的极限位移；Qyj为构件j的屈服剪力为震动开始至t时刻构件j的累积滞回耗能．的表达式为

式中:Fj和Fj+1分别为第j和j+1时刻的剪力；xj和xj+1分别为第j和j+1时刻的位移．

定义基于层的损伤模型为

式中:Df为第f层层损伤值；ωj为构件j的损伤权值，为第f层所有柱子损伤均值．

参考《中国地震烈度表》[10]中给出的震害指数及文献[11]，并结合本损伤模型的特点，定义了对应结构不同破坏等级的损伤指数范围，如表4所示．

表4 不同震害等级对应的损伤指标范围Tab.4Range of damage index corresponding to different damage grades

选择首层两根钢柱来进行损伤分析．参考所用钢材材料及截面尺寸，根据材料力学及结构力学的相关知识可以求得型钢柱的性能参数:屈服应力σy= 235,MPa，截面惯性矩I=383×10-8,m4，屈服弯矩My=15,320,N·m，屈服剪力Fy=39,282.05,N，屈服位移xy=2.028,mm．本试验中对于式(1)中构件的极限位移δuj可以用延性系数μ乘以屈服位移xy的方法确定．根据文献[12]中对钢结构延性的分析，延性系数μ取值在12.0～14.5之间，在没有更多试验数据支持下，并从安全的角度考虑，这里μ取值为12，所以δuj=24.34,m．

图7给出了峰值加速度为1.8g时，3种地震波作用下结构模型首层钢柱的损伤时程曲线，钢柱子的最终损伤值分别为0.415、0.466、0.447，由表4中关于损伤程度的界定可知，该钢柱在3种地震波作用下达到的损伤状态均为严重破坏，3条损伤时程曲线发展情况相似，都是在各自地震波达峰值时，损伤发生明显的突变，之后平稳发展．

图7 结构首层钢柱损伤时程曲线Fig.7 Damage time-history curves of the steel columns on the first story

结构构件局部的损伤过程可以通过粘贴在构件表面的应变片进行评估，但传统的方法往往只简单地判断材料是否发生屈服或者开裂，很多重要的材料信息如应力发展过程、材料性能退化过程却没有得到．本文将除白噪声扫频外各工况同一位置应变连成一列数据，并采用应变反演的方法分析测试点处材料的应力发展过程，即在有限元模型中，将构件离散成一束纤维模型，将贴片处的纤维分离出来，通过有限元程序可以将测量得到的应变时程施加到应变片所在纤维两端，进而通过所分析纤维的应力时程和损伤发展过程反演贴片处构件材料性能的变化过程．图8为首层钢梁端焊缝撕裂情况，结构第2、3层钢梁端损伤情况类似．图9为首层钢柱脚应力发展过程，钢柱脚在第200,s时(对应试验工况为0.7g的Tianjin波)开始发生屈服；400～900,s之间输入的地震波加速度幅值在0.3g～0.5g之间，应力相对较小；900,s以后地震波加速度幅值逐渐增大，钢材应力不断增大，损伤也加大，由于振动台可施加的最大加速度有限，在1.8g的El Centro波和Taft波之后钢柱并没有完全断裂，但已发生严重屈服，应力已达300,MPa．第2、3层的柱子未发生屈服，但与之相连的钢梁端焊缝撕裂．

表5给出了结构模型各层不同工况PGA下的损伤指标及损伤状态．可以看出，结构的首层和顶层的损伤程度与第2层相比较为严重；El Centro波对结构损伤的影响较小；结构各层的损伤值随着PGA的增加而变大，最终将PGA调幅到1.8g时，结构在Tianjin波、Taft波及El Centro波作用下，首层的损伤程度均达到严重破坏，第2、3层的损伤状态均为中等破坏．

图8 首层钢梁损伤状态Fig.8 Damage state of steel beam at the first story

图9 首层钢柱脚应力发展时程Fig.9 Stress time history of column bottom at the first story

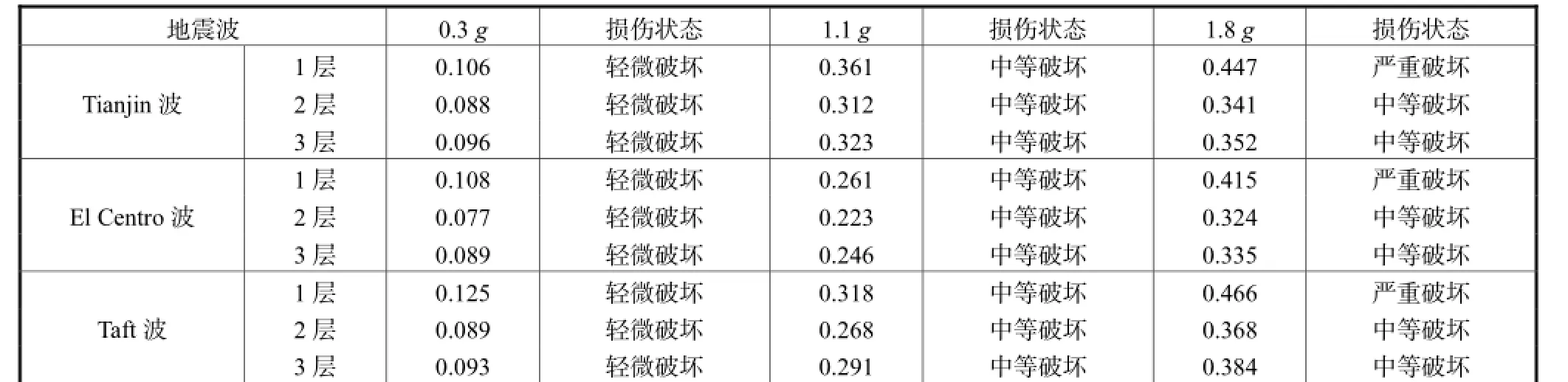
表5 结构各层不同工况PGA下的损伤指标及损伤状态Tab.5 Damage value and damage status of each floor under different PGA levels

由图7及表3中对结构IDA分析的结果可知，表5中损伤程度的界定确定结构未达到倒塌，首层严重破坏，第2、3层中等破坏均与试验结果相符．

3 结 语

通过一个钢-混凝土混合结构的振动台试验，对钢框架结构在强震作用下的动力特性、动力响应及损伤情况的变化规律进行了分析．随着地震强度的增大，结构前两阶自振频率以及层动力放大系数逐渐减小．随着地震强度的增加，结构的塑性程度变大，阻尼增大，刚度降低，损伤加剧，导致结构各层最大位移反应增大，结构顶层加速度动力放大系数减小．选取结构薄弱层钢柱作为损伤分析对象，运用提出的双参数损伤准则对其损伤演化规律进行分析，结合对该模型结构IDA分析的结果以及试验结果，证明提出的双参数损伤准则是合理有效的．

［1］ 张 倩. 钢框架结构基于性能的抗震设计方法研究[D]. 西安:西安建筑科技大学土木工程学院，2008.

Zhang Qian. Research on the Displacement-Based Seismic Design Method of Steel Moment-Resisting Frame [D]. Xi′an:School of Civil Engineering，Xi′an University of Architecture and Technology，2008(in Chinese).

［2］ 李国强，孙飞飞. 关于钢结构抗震存在的问题及建议[J]. 地震工程与工程振动，2006，26(3):108-114.

Li Guoqiang，Sun Feifei. Some problems and suggestions on seismic design of high-rise steel structures [J]. Earthquake Engineering and Engineering Vibration，2006，26(3):108-114(in Chinese).

［3］ 邱法维，钱稼茹，陈志鹏，等. 结构抗震试验方法[M]. 北京:科学出版社，2000.

Qiu Fawei，Qian Jiaru，Chen Zhipeng，et al. Methods of Structure Seismic Test [M]. Beijing:Science Press，2000(in Chinese).

［4］ 徐龙河，单 旭，杨冬玲，等. 考虑损伤累积效应的钢框架结构抗震分析与设计[J]. 天津大学学报，2012，45(6):493-498.

Xu Longhe，Shan Xu，Yang Dongling，et al. Seismic analysis and design for steel frame structure considering damage accumulation effects [J]. Journal of Tianjin University，2012，45(6):493-498(in Chinese).

［5］ 徐龙河，杨冬玲，李忠献，等. 空间钢框架支撑结构损伤定位分析[J]. 天津大学学报，2011，44(7): 577-581.

Xu Longhe，Yang Dongling，Li Zhongxian，et al. Damage localization analysis to spatial steel bracedframe structure [J]. Journal of Tianjin University，2011，44(7):577-581(in Chinese).

［6］ 吕 杨，徐龙河，李忠献，等. 应用纤维单元模型的钢筋混凝土框架结构损伤与失效分析[J]. 天津大学学报，2011，44(10):925-929.

Lü Yang，Xu Longhe，Li Zhongxian，et al. Damage and failure analysis of reinforced concrete frame structure using fiber element model [J]. Journal of Tianjin University，2011，44(10):925-929(in Chinese).

［7］ Vamvatsikos D，Fragiadakis M. Incremental dynamic analysis for estimating seismic performance sensitivity and uncertainty [J]. Earthquake Engineering Structural Dynamics，2010，39(2):141-163.

［8］ FEMA273. NEHRP Guidelines for the Seismic Rehabilitation of Buildings [R]. Washington DC:SAC Joint Venture，Federal Emergency Management Agency，1997.

［9］ 李军旗，赵世春. 钢筋混凝土构件损伤模型[J]. 兰州铁道学院学报，2000，19(3):25-27.

Li Junqi，Zhao Shichun. Damage model of reinforced concrete member [J]. Journal of Lanzhou Railway University，2000，19(3):25-27(in Chinese).

［10］ GB/T 17742—2008 中国地震烈度表[S]. 北京:中国标准出版社，2008.

GB/T 17742—2008 The Chinese Seismic Intensity Scale [S]. Beijing:The Standards Press of China，2008(in Chinese).

［11］ Park Y J，Ang A H S. Mechanistic seismic damage model for reinforced concrete [J]. Journal of Structural Engineering，1985，111(4):722-739.

［12］ 贲庆国. 钢框架结构地震作用下累积损伤分析及试验研究[D]. 南京:南京工业大学土木工程学院，2003.

Ben Qingguo. Analysis of Accumulated Damage of Steel Frame Structures Under Earthquakes and Experiment Study [D]. Nanjing:School of Civil Engineering，Nanjing University of Technology，2003(in Chinese).

Shaking Table Tests and Damage Analysis of a Steel Frame-Shear Wall Model Structure

Xu Longhe1，Shan Xu1，Lü Yang2，Li Zhongxian2
(1. School of Civil Engineering，Beijing Jiaotong University，Beijing 100044，China；2. School of Civil Engineering，Tianjin University，Tianjin 300072，China)

A series of shaking table tests were conducted on a 1∶4 scaled 3-story steel frame-shear wall model structure，and the dynamic characteristics，dynamic response and damage evolution of the steel frame structure under strong earthquakes were analyzed in this paper. Results indicated that with the increase of earthquake intensity，the first two natural frequencies and the layer dynamic magnification factors decreased，and the displacement responses increased. An improved two-parameter damage model for component，which considers the effect of hysteretic deformation amplitude on accumulative damage energy dissipation，was suggested. Structural damage evolution analysis of the weak story was made using this damage model，which was proved to be reasonable and effective with the combined consideration of IDA results and shaking table test results.

steel frame structure；shaking table test；damage model；damage evolution

TU352

A

0493-2137(2013)12-1127-06

DOI 10.11784/tdxb20131212

2012-06-27；

2012-08-14.

国家优秀青年科学基金资助项目(51322806)；国家自然科学基金面上项目(51178034)；高等学校学科创新引智计划项目(B13002).

徐龙河（1976— ），男，博士，副教授.

徐龙河，lhxu@bjtu.edu.cn.