断层破裂速度对地震动影响的离散波数有限元法模拟

胡进军 ，徐龙军 ，谢礼立 ,

(1. 中国地震局工程力学研究所，哈尔滨 150080；2. 中国地震局地震工程与工程振动重点实验室，哈尔滨 150080；3. 哈尔滨工业大学土木工程学院，哈尔滨 150090)

在过去的几十年中，全球范围内发生了数次靠近城市的地震，即所谓的“直下型”或“近直下型”地震，造成了严重的灾害和损失，同时近断层地震动的巨大潜在破坏力也在历次地震中得到了验证．比如1994年的 Northridge地震、1995日本的 Hyogo-Ken Nanbu地震、1999年土耳其的Izmit地震、1999年中国台湾 Chi-Chi地震以及 2010年和 2011年的新西兰 Christchurch地震、2011年的东日本大地震等．这些地震之所以会造成严重灾害的主要原因之一就是地震的近断层效应(比如方向性效应、上下盘效应等)引起的具有巨大潜在破坏力的近断层地震动[1-9]．近断层地震动的概念是为了体现靠近地震断层区的地震动的特殊效应及其对结构潜在的危害性与远离断层区的地震动的区别而提出的．由于近断层区的地震动显著受到断层破裂机制、破裂过程、场点的位置及断层滑动引起的永久地面位移等的影响，靠近断层破裂区的地震动与远离断层区的地震动可能会有明显的差别，即所谓的地震动近断层效应．地震动的近断层效应一般体现在两个方面：一方面是在某个场点地震记录体现出的区别与远场记录的典型特征，比如地震动波形的差异、频谱成分组成的差异和持时长短等参数的差异；另一方面体现在整个近断层区域地表的地震动分布场的特性，即在峰值、谱值参数和持时参数等的分布场的特点[10-11]．

地震断层破裂传播的方向性和震源的辐射模式会引起地震动及其空间分布的一些典型特征，其在单个的地震记录中可表现为时程曲线中的长周期脉冲，在整个地震动的空间分布场可表现为随方位角变化的地震动参数，比如峰值、频谱和持时等，这就是所谓的地震动的方向性效应[10，12-15]．方向性效应的影响因素众多，比如震源机制、破裂速度、破裂传播方向与地震波到场点的射线方向的夹角以及断层的埋深[12-18]等．目前，虽然全世界范围内已经获得了大量的强震记录，但是由于每次地震的强震记录都很有限，且有一定的局限性，不能满足研究参数的变化对方向性效应的影响，因此目前采用数值方法模拟和预测不同震源参数产生的地震动是最为现实可行的研究方法和手段之一．

本文基于建立的典型断层模型，通过改变断层破裂速度参数数值模拟地震动．根据数值模拟结果，分析不同破裂速度对地震动方向性特征的影响，目的是从理论上解释破裂速度对近断层地震动方向性效应影响的基本特征和规律，为地震动场预测以及建立考虑方向性效应的衰减关系模型等提供理论依据．

1 地震动的数值模拟

1.1 数值计算方法和设定地震

本研究采用离散波数有限元方法[19]求解地震波在介质中传播的格林函数，考虑了 P波、S波和面波成分，计算结果是在水平成层地壳介质中的完全反应，然后再根据 Spudich和 Archuleta的方法和表示定理计算有限断层产生的地震动[20]．此方法可以考虑震源机制、破裂速度、断层倾角、滑动分布等参数的影响，因此断层的破裂过程可以设定得比较复杂.另外，此方法与其他有限断层震源模型在水平成层介质中计算地震动的方法相比，可以更有效地计算给定地壳速度结构下的完全反应，其格林函数包含了地壳结构的完全反应，所有 P波、S波和面波以及近场项均包含在计算的结果中，因此该计算方法和程序适用于近断层地震动的数值模拟研究[21-22]．

确定设定地震参数是进行数值模拟的前提．为了选取一个合理的设定地震震级，基于 Wells和Coppersmith[23]、王海云[24]研究中给出的较为可靠的244个地震目录，同时为了便于研究方向性效应，从目录中选取了具有单一走滑震源机制的70个地震的震级参数进行统计，得到所有地震的平均矩震级为6.1级，矩震级的置信区间上限为6.3级．考虑到工程更加感兴趣的走滑断层地震的震级范围，研究假定设定地震的矩震级为6.4级，略高于统计的中值．震级确定后再根据Wells和Coppersmith[23]、王海云[24]、Somerville等[25]以及 Hanks和 Kanamori[26]给出的震级与震源参数之间的经验统计关系，得到矩震级 6.4级设定地震的部分震源参数，见表 1．为了研究不同破裂速度对方向性效应的影响，假定断层的破裂速度分别为 0.700、0.800、0.900和 0.925倍的剪切波速，并且假定破裂速度均一，即破裂过程中破裂速度为常值．

表1 Mw6.4级地震的震源参数Tab.1 Parameters of scenario earthquake Mw6.4

1.2 断层模型、地壳速度结构和观测网格

为了便于研究破裂方向性效应对地震动的影响，假定断层为典型的垂直走滑断层，且假定断层的破裂模式为单侧破裂模型．根据数值计算方法和程序的特点，研究采用笛卡儿坐标系(见图 1)，z＝0为地表，z轴向下，x轴与断层的走向平行，y轴与断层的走向垂直．断层几何模型见图 1，假定断层的上界埋深为 ZF＝1,km，断层的长为 26,km，宽为 10,km．为了简化断层模型，在断层面上采用均匀的滑动分布、上升时间以及不沿断层破裂方向而改变的常破裂速度，并假定破裂起始点在断层下倾方向的中心(见图2)．在传播介质参数方面，假定地壳速度结构为深度的函数，速度模型采用水平成层的速度结构，P波、S波波速和密度参数见表2．

图1 断层几何模型示意Fig.1 Sketch of fault model

图2 断层面上破裂时间的等值线图Fig.2 Contour map of rupture time on fault plane

表2 地壳速度结构模型参数Tab.2 Crustal velocity structure model parameters

由于本文研究的目的是分析不同破裂速度对地震动方向性效应的影响，因此选择了较大的观测区域(见图 3)．在沿着断层走向(x轴)长 120,km 和垂直于断层走向70,km范围内设置了平行于走向的14行观测点，各行之间的间距 5～10,km，靠近断层处的观测点设置得比较密集．考虑到方向性效应等因素的影响，观测点在破裂的前、后方设置得并不对称．在破裂朝向的一侧设置了更多的观测点．地表的观测点共278个．

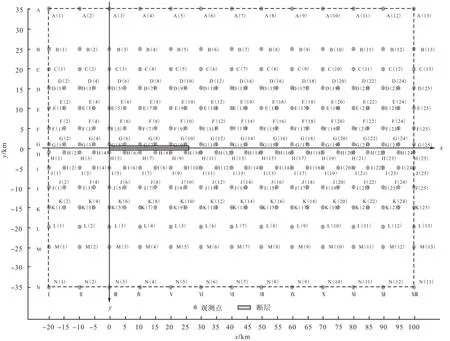
图3 地表观测点分布Fig.3 Distribution of observers on surface

2 地震动的特征分析

基于第1节中的震源模型，计算了地表观测点的3分量，包括垂直于断层走向的分量(FN分量)、平行于断层走向的分量(FP分量)和竖向分量(UP分量)的地震动时程．再根据得到的这些地震动分析方向性效应引起的近断层地震动加速度、速度和位移的峰值、反应谱和能量持时等参数的特征．

2.1 时程特征

为了从地震动时程曲线方面比较不同破裂速度的影响，选取了与断层走向平行排列的一行(G行)观测点的 FN分量加速度时程曲线(见图 4)，并将同一台站记录的不同破裂速度情况下的时程表示在同一个图中，其中虚线代表Vr＝0.700Vs的时程，实线代表Vr＝0.925Vs的时程；并且每条时程的上方分别给出了相应的最大幅值，也就是 PGA，单位为 cm/s2．从图 4可以看出，一方面，断层的破裂速度对地震动加速度的峰值影响很大，随着破裂速度的增大地震动的峰值逐渐增大；另一方面，随着破裂速度的增大，地震动的峰值出现的时间逐渐向后移．

图4 Vr＝0.700Vs和 Vr＝0.925Vs时 G行观测点的加速度时程的对比Fig.4 Comparison of acceleration time history between Vr= 0.700Vs and Vr＝0.925Vs of observers in line G

2.2 峰值特征

地震动的峰值是工程领域最感兴趣的重要参数之一，因此除了从地震动时程来分析破裂速度的影响之外，还可以从峰值沿断层走向的变化来分析和对比其影响．为此，同样选取靠近断层的 G行的 25个观测点，图5给出了G行的25个观测点不同破裂速度下的 FN、FP和 UP分量的加速度峰值 PGA沿断层走向距离 Xs的变化曲线．速度和位移峰值沿断层走向的变化特点与加速度的类似．

图5 PGA沿断层走向的变化Fig.5 Variation of PGA in the fault strike direction

不同破裂速度下的峰值沿断层走向的变化表明以下两点．

(1) 破裂速度对地震动峰值有显著的影响，破裂速度越接近于剪切波速，地震动的峰值越大．当破裂速度为0.900倍的剪切波速时，最大的峰值加速度是破裂速度为0.700倍的剪切波速时的1.6倍．容易理解，当其他震源参数不变时，破裂速度越接近剪切波速，从断层上不同破裂点传播到观测点的地震波的时间间隔就越小，地震动的能量积累效应就越明显，峰值也越大．

(2) 破裂速度对不同分量的峰值的影响程度和对整个地震动场的影响范围不一样，如图 5所示，地震动的 FN分量与 FP分量有明显的差别．一方面，FN分量的峰值明显高于FP分量；另一方面，方向性效应对FN分量和FP分量的控制区域不同．对于FN分量，地震动峰值衰减得非常慢，在破裂前方 3倍的断层长度处峰值依然很高；而对于 FP分量，在破裂前方 1.5倍的断层长度区域地震动的峰值就已经衰减到接近破裂的开端处．因此，破裂速度对 FN分量峰值的影响可表现在从破裂开始到几倍的断层长度的距离处的场点，而破裂速度对 FP分量峰值的影响主要表现在破裂末端附近的有限区域．

地震动峰值场的特征更能直观地说明不同破裂速度的影响，图 6以地震动加速度为例，给出了地震动的 FN分量的 PGA等值线图，图 6(a)～6(c)分别表示破裂速度 Vr＝0.700,Vs、0.800,Vs和 0.900,Vs下峰值场的等值线图．通过对不同破裂速度下峰值场的对比表明，破裂速度对地震动的峰值影响显著，且地震动的峰值随着破裂速度的增大而增大，地震动场的整体幅值也逐渐增大．另外，由于破裂速度的变化对地震动的加速度、速度和位移的各分量峰值场都有相似的影响，故未给出图形．

2.3 反应谱特征

地震动的反应谱也是地震动本身的一个重要参数，为了分析各周期的反应谱值沿断层走向的变化情况，本研究将 G行观测点不同破裂速度下的加速度反应谱 SA沿断层走向距离 Xs的分布表示在图 7中；同时，为了考虑破裂速度对反应谱各周期的谱值沿断层走向变化的影响，将不同周期下各观测点的反应谱值沿断层走向的变化表示在图 7中．由于速度和位移反应谱有类似的特征，故未给出图形．研究结果表明，破裂速度对反应谱的影响主要体现在反应谱谱值的大小上，其对谱形状的影响并不显著；而且破裂方向性使得位于破裂前方的谱值最大，而后逐渐衰减；破裂速度的影响表现在随着破裂速度的增大，反应谱谱值加大，对于加速度、速度和位移的各分量均有相似的结果．

图7 不同破裂速度时加速度反应谱沿断层走向的变化Fig.7 Response spectra in line G for different rupture velocities

2.4 持时特征

地震动的强震动段持续时间(持时)也是表征其工程特性的重要参数，研究表明持时的长短对结构的破坏有重要影响，持时的加长会造成结构的累积变形和累积破坏，同时也会导致某些结构因低周疲劳而丧失局部强度，而且对于地震液化，持时有时起着决定性作用．因此，为了比较破裂速度对地震动持续时间的影响，以地表观测点 G行各点的地震动的 90%相对能量持时[2,10,14]为例，将不同破裂速度时持时 D90沿断层走向距离 Xs的变化和持时场的特征表示在图8和图9中．

图8 不同破裂速度下的能量持时沿断层走向的变化Fig.8 Variation of duration with fault strike direction for different rupture velocities

图9 不同破裂速度的加速度持时等值线图Fig.9 Duration contour map of FN component for different rupture velocities

从图8和图9可以看出：一方面，不同的破裂速度下持时均受到方向性效应的影响，即破裂前方区域内的地震动持时较短，破裂后方区域内的持时较长(这表明，破裂的前方地震动的能量分布比较集中，而在破裂的后方地震动的能量分布比较均匀[12-15])；另一方面，破裂速度对持时沿断层走向的变化影响不明显，随着破裂速度的增加，地震动的持时在破裂前方略有减小，在破裂后方略有增加或者不变，但是破裂速度的变化对持时的影响并不太明显．其主要原因可能在于震级应该是影响地震动持时的最主要因素，而本研究采用的是相同的震级，因此持时在不同破裂速度下的变化不大．

3 结 论

本研究根据设定地震和经验统计关系确定了断层的基本参数，采用近场地震动的数值模拟方法，计算了不同破裂速度下地表设定观测点的地震动时程，研究了地震动的峰值、反应谱和持时3个基本工程参数沿着断层走向的变化以及在整个研究区域地表的分布特征，研究表明断层的破裂速度对地震动的方向性效应有重要的影响．

(1) 在假定的断层破裂速度变化范围内，不同的破裂速度均会对地震动及其空间分布产生明显的影响，地震动的峰值、反应谱和持时在断层破裂前后方向上差别较大，从整体上表现为破裂前方的幅值(包括峰值和反应谱值)大于破裂后方，破裂前方的持时小于破裂后方，因而使得地震动的分布具有明显的方向性．

(2) 从地震动峰值和反应谱参数的等值线分布场上可以发现，在断层末端存在一个典型的区域，此区域内的地震动显著受到了方向性的影响和控制，在区域内的地震动峰值和反应谱值显著高于其他区域，而持时则低于其他区域．此受到方向性显著影响的区域位于断层破裂的前方，具体位置与地震动的分量相关：对于 FN分量，受显著影响的区域可延伸到距离震源 3倍的断层长度甚至更大的范围内；而对于FP分量和 UP分量，其受显著影响的区域在距离震源1.5倍断层的长度左右．

(3) 破裂速度的变化对地震动的方向性特征有重要影响．随着破裂速度逐渐接近于剪切波速，方向性效应越来越明显，破裂速度越接近于剪切波速，地震动的幅值也越大．另外，破裂速度的变化对地震动的加速度、速度和位移参数都有影响，且其对各参数的影响均有上述的特征．

4 讨 论

针对本研究的结论，有两点需要说明和讨论.

(1) 地震动的方向性效应受到众多因素的影响，虽然通过对实际地震动数据来统计分析方向性效应是最直接和可靠的方法，但是目前还很难获取充足的用于研究方向性效应的实际地震动数据；而数值模拟的方法虽然可以给出不同条件下的地震动的方向性效应的特征，但是由于在数值模拟中缺乏对地震震源参数、传播路径等的完全了解，以及数值模拟方法的限制，因此，要想给出定量的结论，还要结合大量的实际地震动数据来验证．

(2) 从本研究数值模拟给出的各图可以看出地震动及其分布的方向性效应非常明显，但是实际地震中可能并不会如此显著和典型．其主要原因在于：一方面，本研究采用了较为简单的震源模型、单一方向的破裂机制、均匀的滑动分布和均一的破裂速度等，这些条件均有利于产生方向性效应；另一方面，实际地震过程非常复杂，地震动受到震源、传播路径和场地等各种因素的影响，因此即使断层的破裂速度接近于震源区介质的剪切波速时，也不一定会造成明显的方向性效应．

致 谢：

感谢国家重点基础研究发展计划(973计划)项目(2011CB 013601)、国家自然科学基金重点项目(51238012，9121530113，50938006)和中国地震局工程力学研究所基本科研业务专项(2011B02)等项目的资助．

［1］ Hall J F，Heaton T H，Halling M W，et al. Near-source ground motion and its effects on flexible buildings[J].Earthquake Spectra，1995，11(4)：569-605.

［2］ Somerville P G，Smith N F，Graves R W，et al. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity[J].Seismological Research Letters，1997，68(1)：199-222.

［3］ Dalguer L A，Irikura K，Riera J D，et al. The importance of the dynamic source effects on strong ground motion during the 1999 Chi-Chi，Taiwan，earthquake：Brief interpretation of the damage distribution on buildings[J].Bulletin of the Seismological Society of America，2001，91(5)：1112-1127.

［4］ Huang C C，Lee Y H，Liu H P，et al. Influence of surface-normal ground acceleration on the initiation of the Jih-Feng-Erh-Shan Landslide during the 1999 Chi-Chi，Taiwan，earthquake[J].Bulletin of the Seismological Society of America，2001，91(5)：953-958.

［5］ Oglesby D D，Day S M. Fault geometry and the dynamics of the 1999 Chi-Chi(Taiwan)earthquake[J].Bulletin of the Seismological Society of America，2001，91(5)：1099-1111.

［6］ Bouchon M，Toksöz N，Karabulut H，et al. Seismic imaging of the 1999 Izmit(Turkey)rupture inferred from the near-fault recordings[J].Geophysical Research Letters，2000，27(18)：3013-3016.

［7］ Schmedes J，Archuleta R J. Near-source ground motion along strike slip faults：Insights into magnitude saturation of PGV and PGA[J].Bulletin of the Seismological Society of America，2008，98(5)：2278-2290.

［8］ Saburoh M，Hiroyuki M，Tomohiro A. Strong motion records from the 2011 off the pacific coast of Tohoku earthquake[C]//Proceedings of the International Symposium on Engineering Lessons Learned from the2011Great East Japan Earthquake.Tokyo，Japan，2012：297-302.

［9］ Hiroyuki M，Isao N，Katsuichirou H. Strong motion records of the great east Japan earthquake observed at Fukushima Dai-ichi nuclear power plant and Fukushima Dai-ni nuclear power plant[C]//Proceedings of the International Symposium on Engineering Lessons Learned from the2011Great East Japan Earthquake.Tokyo，Japan，2012：314-321.

［10］ 胡进军. 近断层地震动方向性效应及超剪切破裂研究[D]. 哈尔滨：中国地震局工程力学研究所，2009.Hu Jinjun. Directivity of Near-Fault Ground Motion and Super-Shear Rupture[D]. Harbin：Institute of Engineering Mechanics，China Earthquake Administration，2009(in Chinese).

［11］ 谢礼立，王海云. 近场地震学中 3个术语译名的商榷[J]. 地震工程与工程振动，2005，25(6)：198-200.Xie Lili，Wang Haiyun. A proposal of Chinese translation of three technical terms in near-field seismology[J].Earthquake Engineering and Engineering Vibration，2005，25(6)：198-200(in Chinese).

［12］ Somerville P，Saikia C，Wald D，et al. Implications of the Northridge earthquake for strong ground motions from thrust faults[J].Bulletin of the Seismological Society of America，1996，86(1B)：S115-S125.

［13］ Somerville P G，Smith N F. Forward rupture directivity in the Kobe and Northridge earthquakes，and implications for structural engineering[J].Seismological Research Letters，1996，67(2)：55.

［14］ Somerville P G，Smith N F，Graves R W，et al. Modification of empirical strong ground motion attenuation relations to include the amplitude and duration effects of rupture directivity[J].Seismological Research Letters，1997，68(1)：199-222.

［15］ Somerville P G. Development of an improved representation of near fault ground motions[C]//Proceedings of the SMIP98Seminar on Utilization of Strong Ground Motion Data. Oakland，CA，USA，1998：1-20.

［16］ Boatwright J，Boore D M. Analysis of the ground accelerations radiated by the 1980 Livermore valley earthquakes for directivity and dynamic source characteristics[J].Bulletin of the Seismological Society of America，1982，72(6)：1843-1865.

［17］ Archuleta R J. A faulting model for the 1979 Imperial valley earthquake [J].Journal of Geophysical Research，1984，89(B6)：4559-4585.

［18］ Abrahamson N A. Effects of rupture directivity on probabilistic seismic hazard analysis[C]//Proceedings of the6th International Conference on Seismic Zonation. Palm Springs，CA，USA，2000：151-156.

［19］ Olson A H，Orcutt J A，Frazier G A. The discrete wavenumber/finite element method for synthetic seismograms[J].Geophysical Journal Royal Astronomical Society，1984，77(2)：421-460.

［20］ Bolt B A.Seismic Strong Motion Synthetics[M].Orlando：Academic Press，1987.

［21］ Spudich P，Xu L. Software for calculating earthquake ground motions from finite faults in vertically varying media[J].International Geophysics，2003，81(B)：1633-1634.

［22］ Lee W H K，Kanamori H，Jennings P C，et al.International Handbook of Earthquake and Engineering Seismology[M]. New York：Academic Press，2003.

［23］ Wells D L，Coppersmith K J. New empirical relationships among magnitude，rupture length，rupture width，rupture area，and surface displacement[J].Bulletin of the Seismological Society of America，1994，84(4)：974-1002.

［24］ 王海云. 近场强地震动预测的有限断层震源模型[D].哈尔滨：中国地震局工程力学研究所，2004.Wang Haiyun. Finite Fault Model for Near-Field Ground Motion Prediction [D]. Harbin：Institute of Engineering Mechanics，China Earthquake Administration，2004(in Chinese).

［25］ Somerville P G，Irikura K，Graves R，et al. Characterizing crustal earthquake slip models for the prediction of strong ground motion[J].Seismological Research Letters，1999，70(1)：59-80.

［26］ Hanks T C，Kanamori H. A moment-magnitude scale[J].Journal of Geophysical Research，1979，84(B5)：2348-2350.