支撑材料超强对弱剪型支撑钢框架影响的研究——兼论抗震钢在弱剪型支撑钢框架支撑构件中的应用

齐永胜，周泓

(1.常州市建设工程结构与材料性能研究重点实验室(常州工学院)，江苏 常州 213002;2.河海大学土木与交通学院，江苏 南京 210098)

在弱剪型中心支撑钢框架体系中，支撑作为抗震的第一道防线，在结构经受强震时，要求其进入屈服状态，以消耗地震能和减小结构刚度削弱地震反应，起到保护整个结构的作用。［1－3］但由于一般钢材屈服强度离散性较大，可能会出现支撑屈服强度较明显高于钢框架的情况(考虑到这种体系使用的普遍性，这种情况可能大量存在)，这时如果支撑在需要屈服的时候由于超强不能屈服则可能会迫使主钢架进入塑性状态，从而使钢框架从第二道防线转变为第一道防线，本应被保护的系统成了保护者，这样便与设计意图大大背离，使结构处于危险状态，或使得震后加固维修变得极为困难，毕竟拆换支撑构件比修复梁柱体系简单、经济得多。目前关于支撑材料超强对弱剪型支撑钢框架影响的研究仍很缺乏，本文以一个简单的算例探讨这个问题，以期抛砖引玉，并建议采用抗震钢制作支撑构件以避免支撑材料超强对弱剪型支撑钢框架的不利影响。抗震钢是特殊性能钢材中的一种，这种钢材屈服平台很长、很稳定，非常适合用在需要准确控制钢材屈服点的部位。

1 算例简介

算例为单跨单层弱剪型中心支撑框架［4－5］，结构形式如图1，l=6000 mm，h=6000 mm，荷载为p=1440 kN，q=50 kN/m，框架的总质量为3180 kN，柱承担的竖向荷载Pc=1590 kN。设防烈度为8度，场地类型为三类。结构选用Q235钢材，E=206000 N/mm2。按弱剪型框架进行设计，采用框架柱截面为H400×360×10×16，梁选用H400×300×8×14，支撑选用 H250×180×8×12，因此实际选用的支撑面积

分析中框架梁柱构件的屈服强度取为fy=235 N/mm2。支撑采用两种材料数据:第一组支撑采用抗震钢制作，可保证材料有准确的屈服点和较长的屈服平台，为方便比较，取屈服强度为fy=235 N/mm2;第二组采用普通钢材，其屈服强度由于材料性能的离散性达到了Q235钢材屈服强度的 1.3 倍，即 fy=235 ×1.3=305.5 N/mm2。第一组反应弱剪型框架的设计初衷，在较大地震作用下，支撑屈服，通过支撑钢材的屈服平台消耗地震能，而且此时由于结构部分材料进入塑性使得刚度降低从而减弱地震反应，保护框架主体的梁柱构件。第二组旨在分析由于材料性能离散性造成支撑钢材超强的情况下，原始的设计意图能否实现。

基本分析设定:①研究对象为平面支撑框架;②材料各向同性、理想弹塑性;③梁柱刚接，支撑杆两端铰接;④忽略支撑杆件的初始缺陷，不考虑支撑杆受压屈曲(采用防屈曲支撑形式);⑤不考虑残余应力;⑥在模型中只考虑柱子的初始平面内缺陷，即在框架柱的中点处有1/1000柱高的水平初始缺陷，几何缺陷直接按节点坐标形式定义。

图1 弱剪型支撑框架

结构抗震性能采用Pushover和时程分析两种方法进行分析。Pushover分析为得到完整的荷载—变形曲线尤其是峰值后下降段采用ABAQUS6.10软件，框架的梁和柱采用B22单元，支撑采用 B21单元。时程分析使用 ANSYS11.0软件，框架的梁和柱采用BEAM189单元，支撑采用LINK8单元，将框架中楼层质量简化为分布于梁柱节点的集中质量，在梁柱节点采用MASS21单元输入楼层质量。在有限元模型中，梁、柱分为10个单元，支撑为二力杆，设置为一个单元;计算中考虑几何非线性与材料非线性。

2 Pushover分析

由图2可看出第一组抗震钢支撑框架在水平地震作用下承载能力达到极限荷载的峰值1060 kN后，承载能力进入一个相当长的屈服流动平台，流动平台对应的水平坐标值在23～132 mm之间，长度为109 mm，在此区域变形逐渐增加，承载能力和刚度基本保持不变，结构具有非常好的耗能能力，地震时可以充分利用此流动平台消耗地震能，削弱地震反应，保护主框架结构。由随后的时程分析过程可以更明确地看到这一点。

第二组普通钢支撑框架水平承载能力极限值为1220 kN，高于第一组抗震钢支撑框架的相应值。这是因为钢支撑材料超强30%，推迟了塑性变形的发展，使得结构在弹性状态的工作阶段略大于第一组抗震钢支撑框架。普通钢支撑框架在水平地震作用达到水平承载能力极限值后，结构的承载能力立刻下降，没有屈服流动平台，这使得结构的耗能能力明显低于抗震钢支撑框架，因而抗震性能不佳，可能不能实现弱剪型框架的设计意图。

图2 不同钢支撑框架Pushover曲线

3 时程分析

3.1 地震波选取

选取El Centro地震波(如图3所示)进行计算，输入地震波峰值加速度，按照设防烈度为8度的罕遇地震取值，即将地震记录的峰值调整为0.4 g(400 cm/s2)，取地震时间历程的前30 s，在计算中时间积分步长取为△t=0.02 s。在支撑框架的水平方向输入地震波加速度。

图3 El Centro地震波

3.2 时程计算结果及对比分析

1)两种框架基底剪力—柱顶位移(图4)

抗震钢支撑框架地震波作用下框架承受的基底剪力要小于强剪型，框架更早进入塑性阶段后，对塑性变形的需求较大，滞回环饱满稳定，曲线所包围的面积大，表明其具有良好的耗能能力。

普通钢支撑框架在地震荷载作用下，产生的基底剪力较大，虽然也有屈服现象发生，但其滞回环封闭部分所包络面积明显小于抗震钢支撑框架，表示耗能能力远小于抗震钢支撑框架，由此可见钢材性能离散性造成的超强对弱剪型中心支撑框架的抗震性能是不利的，如果采用抗震钢来制作支承构件，就能可靠地避免这种现象，很好地实现设计意图。

图4 基底剪力—柱顶位移

2)两种框架中心支撑滞回环(图5)

两种框架中心支撑滞回环都能达到对应的钢材屈服强度，表明强震作用下，中心支撑都进入了屈服阶段，结构的塑性耗能能力主要来自中心支撑的塑性发展(由两种框架中心支撑滞回环与基底剪力—柱顶位移相似性也可看出此点)。但两种支撑进入屈服状态的时间不同，造成了滞回环封闭程度和包络面积的不同，使得耗能能力有明显差异。在强震作用下抗震钢支撑框架的支撑及时地按设计意图进入了塑性状态，滞回环饱满稳定，包络面积大;普通钢支撑框架的支撑由于超强推迟了对塑性状态的进入，在更大的地震荷载作用下才进入塑性，因而滞回环封闭程度有限，包络面积明显小于抗震钢支撑框架，使普通钢支撑框架未能很好地贯彻设计意图，其抗震能力明显减弱。

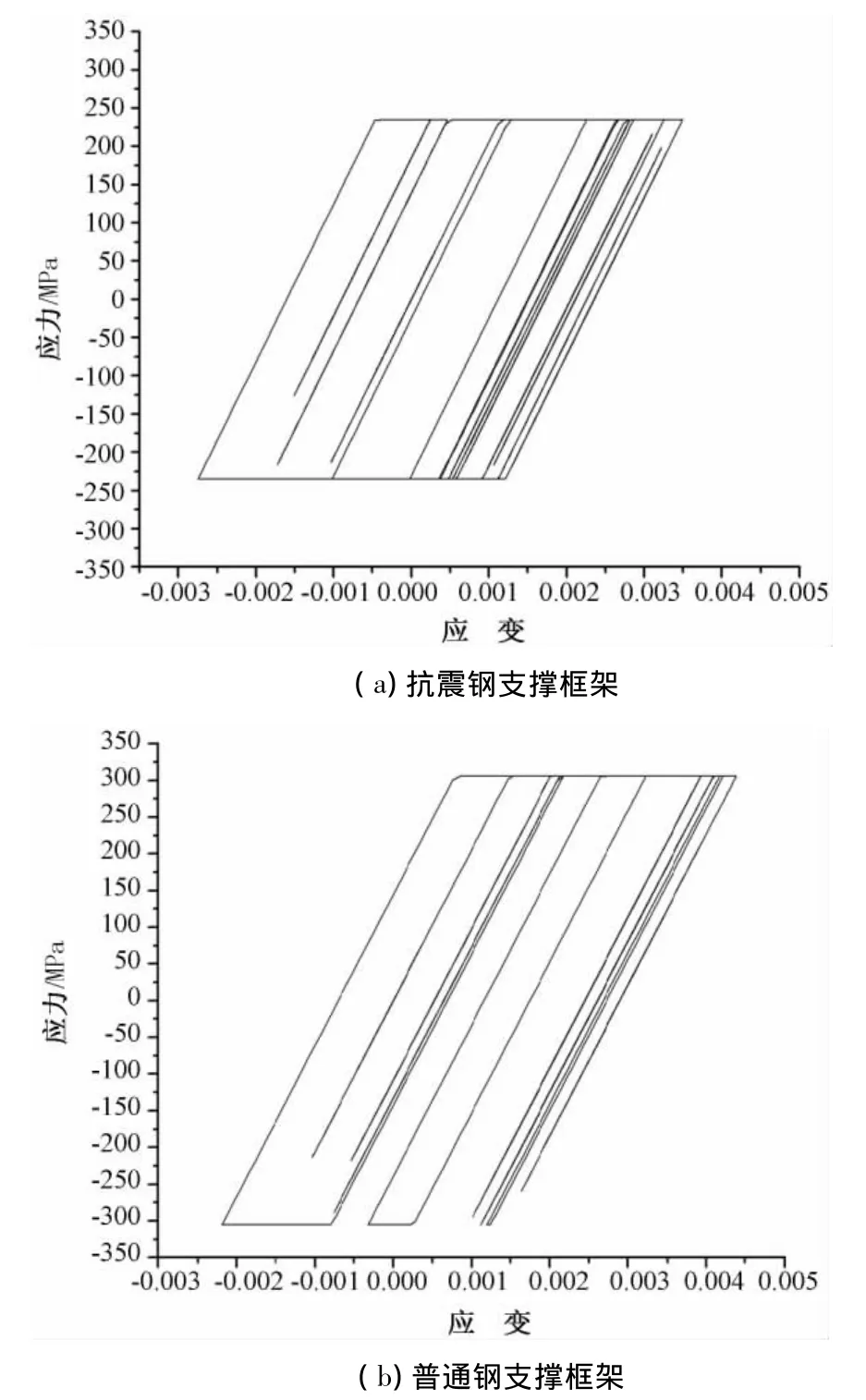
图5 中心支撑滞回环

3)框架右柱顶部水平位移响应(图6)

在El Centro波作用下，抗震钢支撑框架和普通钢支撑框架右柱顶部水平位移时程反应曲线形状相似，在数值上则是普通钢支撑框架水平位移为64.9 mm，大于抗震钢支撑框架51.6 mm。可见普通钢支撑框架局部(支撑构件)强度大了，而地震反应也增加了。这是由于采用抗震钢作支撑的钢框架在较大地震作用下忠实地按设计意图及时地进入塑性状态，靠材料的塑性消耗地震能，并通过刚度的减小削弱地震反应;而普通钢框架由于支撑钢材的超强，当地震使支撑材料达到屈服强度时未能进入屈服流动平台，从而延长了结构的弹性状态，结构刚度未能及时下降，故而地震反应较大，这对保护框架主体是不利的，偏离了设计初衷。

当地震烈度更大时，可能会导致框架梁柱的最不利位置先于支撑进入塑性状态，从而使框架保护了支撑，而不是支撑保护了框架，结构的两道抗震防线次序颠倒，不能发挥支撑的抗震和耗能作用，增加了结构地震危险性。

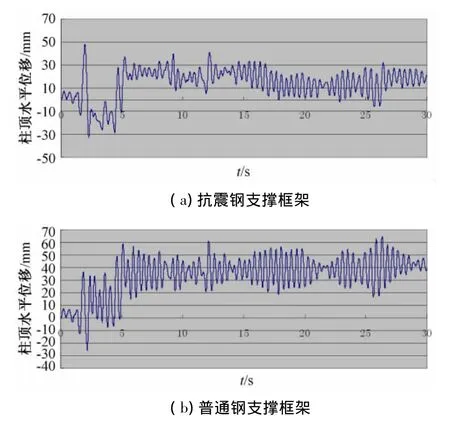
图6 El Centro波作用下框架右柱顶部水平位移响应

4)框架应力分布

分别截取结构在时程分析中达到最大位移时的Mises等效应力云图，如图7所示，在反应过程中，出现较大应力的部位为:左柱柱根单元内侧、右柱柱根单元外侧、右柱柱头梁柱连接内侧。

可以看出，支撑超强的普通钢支撑框架，柱中塑性发展明显多于抗震钢支撑框架，其原因是未能充分发挥支撑耗能作用，地震能量在结构中逐渐积累，最终需要主框架较多地进入塑性以消耗地震能，使结构震后的残余变形增大，加大了修复难度和费用，并且增加了在更大地震下倒塌的可能性。

图7 最大位移时的Mises等效应力云图

4 结语

1)Pushover和时程分析的计算表明，在弱剪型中心支撑框架中采用普通钢材制作钢支撑可能因钢材超强使支撑未能按设计意图及时进入塑性状态，不能充分支撑塑性耗能能力，以减小地震反应，保护主体结构，从而使得钢框架遭受较大破坏，不能担负第一道防线的作用，增大了结构在地震中的危险性。

2)采用抗震钢作弱剪型中心支撑框架的支撑可以很好地贯彻设计意图，使支撑构件在预定地震强度作用下进入塑性状态，通过钢材的塑性屈服流动消耗地震能，降低结构刚度减小地震反应，使得中心支撑构件成功地担负起第一道抗震防线的作用，起到“保险丝”的作用，有效地保证框架主体的安全。虽然抗震钢价格较高，但支撑构件占结构整体比重很小，由此增加的造价是很有限的，与安全性和抗震能力的提高相比可以说是性价比极高的举措。

［1］杨俊芬.中心支撑钢框架的结构影响系数和位移放大系数研究［D］.南京:河海大学，2009:89－95.

［2］杨俊芬.用增量动力分析方法求解人字形中心支撑钢框架的结构影响系数和位移放大系数(Ⅰ)——方法［J］.地震工程与工程振动，2010，30(2):64 －71.

［3］杨俊芬.用增量动力分析方法确定人字形中心支撑钢框架的结构影响系数和位移放大系数(Ⅱ)——算例［J］.地震工程与工程振动，2010，30(3):86 －95.

［4］童根树.钢结构设计方法［M］.北京:中国建筑工业出版社，2007:80－81.

［5］米旭峰.支撑框架与竖缝剪力墙抗震设计研究［D］.杭州:浙江大学，2007:18－24.