利用小波分析的电流测试方法实现模数混合电路的故障诊断

2013-01-15方玉龙吕洪善

常州工学院学报 2013年1期

方玉龙，吕洪善

(亳州职业技术学院，安徽亳州 236800)

0 引言

随着模拟/数字混合电路设计技术的飞速发展，以及超大规模集成电路和模拟/数字混合电路信号的广泛运用，在片上系统(SOC)中集成各种模数转换、数模转换、锁相环等混合信号电路必然成为未来的发展趋势。因此，对模拟/数字混合电路的诊断和测试提出了日益紧迫的需求。众多研究证实，电流测试法在数字电路故障诊断中是一种行之有效的方法，但是在模拟/数字混合电路中采用电流测试法快速查找故障是当前面临的难题之一。

稳态电流(IDDQ)测试方法是Levi于1981年提出的，该方法不仅受到了业界的重视，也为IDDQ测试奠定了基础，并获得了广泛的运用。最初采用稳态电流测试判断电路的好坏是通过测量稳态漏电流与阈值比较来实现的。随着电子工艺技术的提高，集成电路向深亚微米发展，芯片的漏电流增大，导致正常电路与故障电路的漏电流差别缩小出现重叠，以前采用固定阈值来判断电路是否正常的方法现在则很难再区分，因此，由于工艺原因造成故障检测难度较大。如，CMOS电路中的部分开路故障采用静态电流方法无法判断电路是否正常，因此业界开始考虑采用动态电流测试方法来判断电路是否正常，目前瞬态电流(IDDT)测试只是作为电流测试方法的一种有效补充措施。在模拟/数字混合信号电路故障诊断中采用电流测试方法尚处初始阶段。实际电路中本文提出的电流测试方法有助于快速实现电路故障的检测与定位。诊断过程中应注意不同的生产工艺及电流测试方法对电路诊断的影响。

电路故障诊断过程中的关键问题是对电流测试信号采用什么样的分析方法便于问题的解决。由于小波分析具有良好的时域、频域局部特性，非常适合测试电路中正常信号夹杂了瞬间故障信号，并且将其瞬间故障信号展示出来，比单独的时域分析方法或单独的频域方法更好，便于对故障的定位与检测。因此，提出基于小波分析的动态电流测试方法，实现模拟/数字混合信号电路的故障诊断。

1 故障诊断理论与方法

1.1 小波变换

小波变换是上世纪80年代末发展起来的一种信号分析方法，是适用于分析短持续时间高频分量信号和长持续时间低频分量信号的强有力工具。其优点在于分析信号的局部特征，因此获得“数学显微镜”的称号。

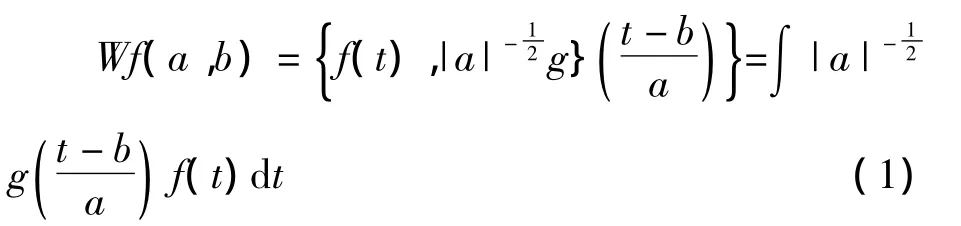
其中，g为小波函数;a为小波伸缩因子;b为平移因子;f(t)为被测信号。经过傅氏变换，可得到小波的频域表达式:

本文提出的电路故障诊断方法，主要是采用测试动态电流参数作为电路故障检测的手段，其测试方法有助于实现电路的准确测试及故障的诊断。故障诊断中如何在被测模拟/数字混合电路的电流信号中，提取出内部缺陷的特征信息是实现故障诊断必须解决的问题。鉴于小波变换在处理信号方面的优势，结合动态电流测试方法来实现故障诊断，按照图1所示故障诊断流程图即可实现混合信号电路的故障诊断。

图1 混合信号故障诊断流程图

1.2 基本算法

针对模拟/数字混合电路的电流信号经测试采样后为离散序列，其用于测试电流信号的最基本配置如图2所示，激励源可以是方波、正弦波或随机信号(由信号发生器根据测试需求产生)，输出响应则从被测电路中提取故障电路的有效特征信息，进而判断故障的存在与否及其故障位置。信号处理采用小波变换算法分析此信号，即使用多分辨率分析的方法对采样动态电流的离散信号进行分解。

图2 测试混合信号的基本配置

设原始采样信号为c0，则此算法可描述为:

其中，g0(n)为包含较多电路全局信息的低频信号，主要用来提取原始信号，由小波基函数构成的滤波器组;g1(n)为包含较多电路局部细节信息的高频信号，主要用来提取原始的细节信号，也是由小波基函数构成的滤波器组;cj+1，k和dj+1，k分别为尺度为j+1下的低频信号和高频信号下的第k个系数。采用此基本算法，对采样后的离散动态电流信号进行多级变换，分解为子空间的高频细节和低频部分，然后低频再继续分解下去得到小波系数:

此系数即模数混合信号电路故障诊断所需的特征系数。其中n为多重小波分解的层数，cAn和cDn分别为第n层分解后概貌分量和细节分量的分解系数，cDn-1，…，cDi，…，cD2，cD1则分别为第n-1层到第1层的细节分量的分解系数。

1.3 故障检测

首先对正常电路的动态电流采样，经过小波分解得到相应的小波系数。模拟/数字混合电路被测电路(CUT)的动态电流信号包含有稳态电流和瞬态电流，采用小波变换对此信号分解也可以得到小波分解系数，此即故障诊断中所包含的电路特征信息。此系数与正常电路的小波系数进行对比，便可确定电路的正常与否。计算误差的度量值常采用均方根误差(RMSE)，采用式(5)比较被测电路和正常电路的小波系数，可以检测出该类故障。

其中，Fi为被测电路的系数;Gi为正常电路的系数。

当然为了便于比较，也可以采用均一化计算normRMSE，比较出小波分析方法和纯频域分析方法的故障敏感度。normRMSE数值的大小反映电路故障检测灵敏度的高低。

1.4 故障定位

通过测试动态电流，经小波变换不仅可以实现故障诊断，还可以对电路故障区域进行精确定位。由于动态电流的正常电路与故障电路存在区别，因此小波分析能够提取信号特征得到相应的小波系数，对电波进行准确的诊断。若被测电路诊断出故障，可进一步测量Td，从而定位故障所处区域。

2 诊断实验

为了说明问题，拟采用小波分析处理动态电流的模拟/数字混合信号电路，故障诊断中测试图如图3所示的2位模数转换ADC电路，检测故障方法如图3所示。

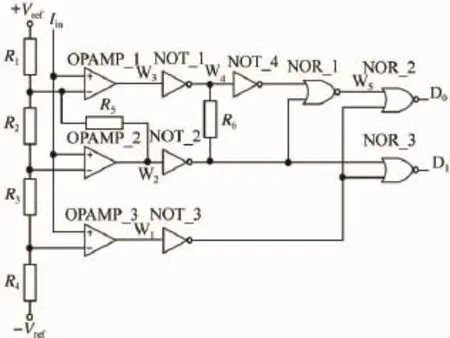
图3 2位模数转换ADC电路图

为了说明问题，首先对传统的单一时、频域(FFT)分析方法和基于小波变换的动态电流故障检测方法进行比较，给被测电路施加一测试信号，得到正常电路以及图3中2位ADC电路故障对应的动态电流信号，其动态电流获取如图4所示。然后分别使用小波分析和FFT对采样信号处理，得到相对应的分解系数和傅氏级数后，代入式(7)进行计算，结果如表1所示。针对图3所示的ADC电路中的桥接故障和开路故障，采用小波变换得到的normRMSE数值远远大于采用FFT算法的数值。由此可见，基于小波分析的动态电流测试方法对电路故障比基于FFT方法具有较高的灵敏度。

图4 动态电流小波测试图

表1 FFT和小波分析灵敏度比较

为了比较单纯时域分析方法(积分法)和基于小波变换的动态电流故障检测方法的优缺点，在电路中任意设置开路故障50个、桥接故障40个、门开路故障10个，通过表2统计数据得知，纯时、频域分析方法检测故障覆盖率要比基于小波变换的动态电流故障检测方法低。通过表1、表2分析可知，采用小波变换对故障的灵敏度和故障的覆盖率要比单独采用纯频域方法或纯时域方法高得多，纯频域方法或纯时域方法难检测的故障，可以通过小波变换分析方法来实现故障的检测。

表2 积分法和小波分析故障覆盖率比较

同样对于上述开路故障50个、桥接故障40个、门开路故障10个进行故障定位，先测量其故障电路的动态电流，再按式(7)算法，通过小波系数的延时参数进行故障定位。表3列出了各个单故障电路的诊断结果。

表3 故障检测和定位结果

从表3可以看出，故障数的检出率明显高于故障数的定位率。主要原因是电路中的某些故障对动态电流的变化无明显影响。小波系数的RMSE在计算时大于阈值，但没有引起延时参数的明显变化，从而导致定位的无效性。由以上内容可知，基于小波分析的动态电流测试方法，不仅能够诊断电路中的故障，具有很高的故障覆盖率，而且能够实现被测电路中大多数故障的定位。