蒙特卡洛模拟优化鲍曼不动杆菌感染的治疗方案

刘佳，许建国，陆强 （江苏省苏北人民医院药剂科，江苏 扬州 225001）

鲍曼不动杆菌是不发酵糖的革兰阴性杆菌，具有强大的获得耐药性和克隆传播的能力，多重耐药（multi－drug resistance，MDR）、广泛耐药（Extensively－drug resistence，XDR）、全耐药鲍曼不动杆菌（Pan－drug resisitence，PDR）呈世界性流行［1］，已成为我国院内感染最重要的病原菌之一。2010年中国CHINET监测数据显示不动杆菌对头孢哌酮／舒巴坦耐药率为30.7%、米诺环素为31.2%，其他大多数抗菌药物的耐药率均在50%以上。2011年“中国鲍曼不动杆菌感染诊治和防控专家共识”提出了国内针对鲍曼不动杆菌感染的治疗首选头孢哌酮舒巴坦，并根据药动／药效学（pharmacokinetics／pharmacodynamics，PK／PD）理论制定合理给药方案。单纯的耐药监测无法了解药物的剂量时间效应关系，所以优化抗生素治疗的策略，对改善致病的微生物学结局和防止细菌耐药非常关键［2］。

药物临床研究的计算机模拟，是近年来兴起的一门交叉学科，运用计算机模拟技术，可以揭示设计中变量和假设对结果的影响，预测和评价不同研究方案可能产生的结果，为制订研究方案提供客观令人信服的证据。美国FDA提倡用电脑模拟方法来制定临床的给药方案，蒙特卡洛模拟法（Monte Carleo simulation，MCS）在化学及多种自然科学中应用广泛［3－4］，在抗菌药物的临床研究中，可用其模拟PK／PD模型优化给药方案［5－8］。以下以此评价头孢哌酮／舒巴坦对鲍曼不动杆菌感染的给药方案，为临床用药提供科学的客观依据。

1 材料与方法

1.1 细菌耐药监测 头孢哌酮舒巴坦（2∶1）对于鲍曼不动杆菌的最低抑菌浓度（MIC）和耐药率、敏感率分布数据引自2005年中国十五家教学医院的耐药性分析［9］和2010年CHINET中国鲍曼不动杆菌耐药性监测［10］。头孢哌酮舒巴坦对鲍曼不动杆菌的 MIC和耐药率数据：MIC5016μg·mL－1，MIC9064 μg·mL－1，R为30.7%。

1.2 给药方案 2011年中国鲍曼不动杆菌专家共识中提出，对于一般感染，舒巴坦的常用剂量不超过4.0g·d－1，对 MDRAB、XDRAB、PDRAB感染国外推荐可增加至6.0g·d－1，甚至8.0g·d－1，分3～4次给药［2］。由以上的给药方案，对于头孢哌酮舒巴坦（2∶1）给出4种给药方案，3 g／q6 h ivd；3 g／q8 h ivd；6 g／q6 h ivd；6 g／q8 h ivd。

1.3 药动／药效学模型 抗菌药物可分成时间依赖性和浓度依赖性两类。前者的杀菌速率与游离药物浓度超过MIC的时间密切相关，其PK／PD指数是血药浓度大于MIC的时间间期与给药间期之比（f%T＞ MIC，即药物浓度超过MIC的时间占给药间隔的百分率；后者的PK／PD指标是峰浓度Cmax或药时曲线下的面积与MIC的比值，即Cmax／MIC和AUC／MIC。头孢菌素类抗生素为时间依赖性，体外实验和动物实验表明头孢菌素／单环类抗菌药物的f%T＞MIC大于40%，就可以达到较好的杀菌作用［8］。因为MIC是体外条件下测定游离药物的浓度，而药动学往往是测定总血浆的药物浓度，只有未与蛋白结合的游离药物才具有抗菌活性。因此用血浆蛋白结合率（protein bounding，PBs）将总血药浓度转化成游离浓度，以前缀f（fraction of drug，游离分数f＝l－PBs）来表示。按一室模型处理时［11］：

Dose为给药剂量；f为游离药物分数；Vd为表观分布容积；t1／2为生物半衰期；τ为给药间隔。各药物的药动学参数t1／2和Vd，引自头孢哌酮舒巴坦（2∶1）的国外药动学研究数据［13］，PBs数据引自《新药临床药理与应用手册》［12］，头孢哌酮舒巴坦的健康人体药动学参数［13］：t1／2为 （1.6±0.3）h，Vd为 （10.2±1.0）L，PBs为0.7～0.9。

1.4 蒙特卡洛模拟 模拟采用Crystal Ball软件（美国Decisioneering公司），采用随机化统计模型和蒙特卡洛模拟为手段，假定药动学参数服从对数正态分布，游离药物分数f服从均匀分布，MIC服从离散分布，使用5 000例次模拟，用模拟出来的中靶概率（probability of target attainment，PTA ），作为评价指标越高越好。PTA＞90% 可选为给药方案。

2 结果

2.1 MCS结果 根据药效学指标的杀菌靶值，模拟获得头孢哌酮舒巴坦各治疗方案的中靶概率和PK／PD指数模拟预测的统计值。3 g／q6 h，3 g／q8 h，6 g／q6 h和6g／q8 h这4种给药方案：达到最佳治疗效果f%T＞MIC大于40%的中靶概率分别如下表所示：92.04%、77.90%、99.63%、97.04%，不同给药方案对鲍曼不动杆菌的（MIC50＝16μg·mL－1）的中靶概率如图1～4所示。

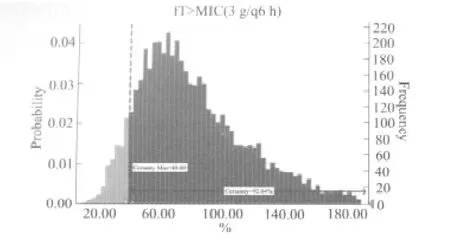
图1 头孢哌酮舒巴坦3 g／q6 h给药时对鲍曼不动杆菌的中靶概率Fig 1 The probability of target attainment（PTA）against Acinetobacter baumanni in the regimen of cefoperazone sulbactam under 3 g／q6 h

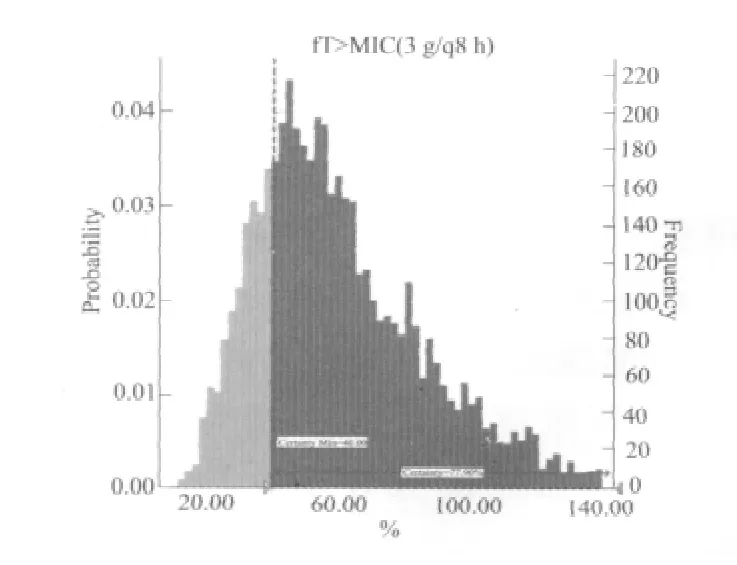
图2 头孢哌酮舒巴坦3 g／q8 h给药时对鲍曼不动杆菌的中靶概率Fig 2 The probability of target attainment（PTA）against Acinetobacter baumanni in the regimen of cefoperazone sulbactam under 3 g／q8 h

图3 头孢哌酮／舒巴坦6 g／q6 h给药时对鲍曼不动杆菌的中靶概率Fig 3 The probability of target attainment（PTA）against Acinetobacter baumanni in the regimen of cefoperazone sulbactam under 6 g／q6 h

图4 头孢哌酮／舒巴坦6 g／q8 h给药时对鲍曼不动杆菌的中靶概率Fig 4 The probability of target attainment（PTA）against Acinetobacter baumanni in the regimen of cefoperazone sulbactam under 6 g／q8 h

2.2 敏感性分析结果 对影响以上给药方案治疗效果的因素进行敏感性分析见表1，从表1可见对头孢哌酮舒巴坦的f%T＞MIC中靶概率影响较明显的参数敏感度。结果表明，t1／2和f对中靶概率影响是正相关，即t1／2越长，f越大，中靶概率越高；而MIC和给药间隔对中靶概率影响负相关，即MIC越低，给药间隔越短，中靶概率越高。t1／2，f和MIC等是药物特有的PK／PD参数无法调整，因此只有缩短给药间隔来提高中靶概率和疗效。敏感性分析结果表明不同给药方案的给药间隔影响也存在差异，6 g剂量给药时给药间隔的影响相当（－7.8%和－7.5%）；而3 g剂量给药时，q6 h和q8 h的差异明显分别为－5.9%和－13.8%。说明同样较低剂量给药时，给药间隔缩短更能增加疗效。

表1 敏感性分析结果（%）Tab 1 Results of sensitivity analysis（%）

3 讨论

蒙特卡洛模拟结果显示：头孢哌酮舒巴坦治疗鲍曼不动杆菌在静脉滴注给药途径下按照3 g／q6 h，6 g／q6 h 和 6 g／q8 h方案给药时中靶概率高（PTA＞90%），模拟表明增加给药次数和给药剂量可以提高药物对鲍曼不动杆菌的杀菌效果，这与2011年中国鲍曼不动杆菌专家共识中的抗菌药物治疗原则相符合。各参数对于模拟结果的敏感性分析表明：MIC及其分布对PTA的影响最大，达到50%以上；药动学参数t1／2的影响约为15%以上；此外头孢哌酮舒巴坦的血浆蛋白结合率较高，敏感性分析结果表明该因素也影响中靶效率。排除药物的PK／PD因素外，影响治疗结果的显著因素是给药间隔，给药剂量对于PTA的影响可以忽略，分析原因可能为头孢哌酮舒巴坦是时间依赖型且较短PAE的抗菌药物，该类药物的抗菌作用受峰浓度影响较小，主要评价参数是T＞MIC。结果表明头孢哌酮舒巴坦治疗鲍曼不动杆菌时应该缩短给药间期以提高疗效。按照3 g／q6 h，6 g／q6 h和6 g／q8 h方案给药时均能达到较好的治疗效果（PTA＞90%），推荐临床以3 g／q6 h的方案静滴给药兼顾了提高抗菌疗效和降低治疗成本问题。

为提高临床疗效，减少耐药菌的产生，可运用蒙特卡洛模拟优化给药方案的设计。该法根据药动学和药效学模型，通过预测并比较不同给药方案的中靶概率或累积反应分数，为用药再评价和进一步调整提供更为科学和客观的依据，给临床优化抗菌药物的治疗方案提供新的研究方法。

［1］Peleg AY，Seifert H，Paterson DL.Acinetobacter baumannii：emergence of a successful pathogen［J］.Clin Microbiol Rev，2008，21：538－582.

［2］陈佰义 何礼贤 胡必杰，等.中国鲍曼不动杆菌感染诊治与防控专家共识［J］.中华医学杂志，2012.92（2）：76－85.

［3］吴洪特，廖森，吴文伟.蒙特卡罗法用于多指标试验设计的优化计算［J］.计算机与应用化学，2007，24（7）：929－931.

［4］张波，朱珠.蒙特卡罗模拟在抗生素药动学和药效学中的应用［J］.中国药学杂志，2008，43（4）：341－344.

［5］史军.药物动力学和药效动力学在抗菌药物新药开发和临床治疗上的应用［J］.中国临床药理学与治疗学，2007，12（2）：121－133.

［6］Wang H，Zhang B，Ni Y，et al.Pharmacodynamic targetattainment of seven antimicrobials against Gram－negative bacteriacollected from China in 2003 and 2004［J］.Int J Antimicrob Agents，2007，30（5）：452－457.

［7］于广华，高璀乡，李芳，等.亚胺培南和左氧氟沙星给药方案蒙特卡洛模拟的比较［J］.计算机与应用化学，2009，26（11）：1467－1470.

［8］Kuti JL，Nightingatle CH，Nicolau DP.Optimizing pharmacodynamic target attainment using the MYSTIC antibiogram：data collected in North America in 2002［J］.Antimicrob A－gents Chemother，2004，48（7）：2464－2470.

［9］杨启文，徐英春.2005年中国十五家教学医院院内获得革兰阴性病原菌耐药性分析［J］.中华医学杂志，2007，87（39）：2753－2758.

［10］习慧明，徐英春.2010年中国CHINET鲍曼不动杆菌耐药性监测。中国感染与化疗杂志，2012，12（2）：98－104.

［11］ Mouton JW，Dudley MN，Cars O，et al.Standardization of pharmacokinetic／pharmacodynamic（PK／PD）terminology for anti infective drugs：an update［J］.J Antimicrob Chemother 2005，55（3）：601－607.

［12］张石革，孙定人.新药临床药理与应用手册［M］.2版.北京：化学工业出版社，2007：607－609.

［13］Reitberg DP，Marble DA，Schultz RW，et al.Pharmacokinetics of cefoperazone（2.0g）and sulbactam （1.0g）coadministered to subjects with normal renal function，patients with decreased renal function，and patients with end－stage renal disease on hemodialysis［J］.Antimicrobial agents Chemothe，1988，32（4）：503－509.