近距爆炸作用下叠层复合夹芯板局部层裂破坏的理论研究

唐 廷，韦灼彬，朱 锡，侯海量

(1.海军工程大学 勤务学院，天津 300450;2.海军工程大学 舰船工程系，武汉 430033)

为抵御或减少爆炸与冲击对结构的破坏作用，现代舰艇多在其关键部位采用复合材料和复合结构，以增强战时生存能力。而复合夹芯结构具有较好的抗爆抗冲击特性，是当前应用较多的一种防护舱壁结构形式。而根据不同的夹芯结构形式和不同的夹芯材料，复合夹芯结构可以分为不同的种类。按结构形式主要可以分为蜂窝细胞结构［1-2］和叠层板结构［3］两种，而夹芯结构(包括面层和内核)常用的材料类型主要有玻纤、碳纤维、Kelvar［4］和超高分子量聚乙稀纤维［5］等为主体的纤维增强复合材料，以及以泡沫铝［6］为代表的泡沫类材料。本文以复合材料为内核的叠层夹芯板为研究对象，运用波动理论计算其在近距爆炸作用下的层裂破坏。

虽然当前国内外复合夹芯结构抗爆的研究成果非常多，但针对叠层复合夹芯板的理论研究成果并不多。Liviu 等［7］和 Terry等［8］给出了各向异性复合夹芯板的三维位移场和运动方程，求解了夹芯平板［9-10］、夹芯曲板［11］和含可压缩核的夹芯板［12］在爆炸荷载作用下的线性与非线性动力响应。Kazancı［13］理论计算了各向同性复合夹芯板在不同脉冲荷载作用下的动力响应。但这些理论均属于弹塑性动力学范畴，适合求解夹芯板的整体响应，不能用于计算夹芯板在爆炸冲击荷载作用下的局部层裂破坏(下文中实验结果)。因此叠层复合夹芯板的局部破坏研究应考虑爆炸冲击波的传播过程。

目前，防护工程领域的研究人员已对夹芯结构或多层介质中的冲击波传播问题进行了初步的研究。研究的主要手段为数值仿真［14-15］，或辅以简单的应力波透射分析［16］，缺乏准确的理论分析。本文结合实验结果，运用应力波理论研究爆炸冲击波在夹芯板中的传播特性，计算夹芯结构中核心材料的破坏机理。研究成果不仅可以为夹芯防护结构的设计提供参考，而且可以为多层介质中波的传播研究提供指导。

1 叠层复合夹芯板抗爆实验

叠层复合夹芯板的抗爆试验在海军工程大学爆炸筒内进行。试验对象为两层钢板和一层玻璃钢板的夹芯结构，结构的平面尺寸为0.7 m×0.7 m，两层钢板的厚度均为0.001 m，而玻璃钢板厚度为0.009 5 m。试验设置如图1所示，装药位置为钢板的中心处，炸药为TNT炸药，质量W=0.4 kg，炸药中心距离结构表面R=0.213 62 m。夹芯板四周通过24个螺丝固定，夹芯板的边界被钢条支座夹持，相当于固支的边界条件。而钢条宽为0.1 m，所以夹芯板的实际迎爆面积为0.5 m ×0.5 m。

图1 试验设置Fig.1 Experimental setup

爆炸后的效果见图2，其中(a)为第一层钢板，(b)为第二层钢板，(c)为玻璃钢夹芯的迎爆面，而(d)为玻璃钢夹芯的背爆面。从中可以看出，第一层钢板的变形相对较小，其中心部分存在较小的环形褶皱变形，而固支边界也存在较小的拉伸变形;第二层钢板的变形相对较大，变形轮廓图见图3，其中心局部明显向外隆起，而固支边界也存在明显的拉伸变形;玻璃钢夹芯的迎爆面仍保持完整，但背爆面中心局部存在明显的剥落破坏(如图4)，经游标卡尺多次测量，剥落层的最大厚度为2.2 mm。而大面积的淡色区域代表了胶体与纤维的粘结破坏。

实验中复合夹芯层背爆面的层裂破坏类似于防护工程中坑道在爆炸荷载作用下的顶部震塌破坏，属于结构的局部破坏问题，宜使用应力波理论进行计算。

图2 试验结果Fig.2 Experimental results

图3 第二层钢板变形轮廓图Fig.3 Profile of the second steel plate

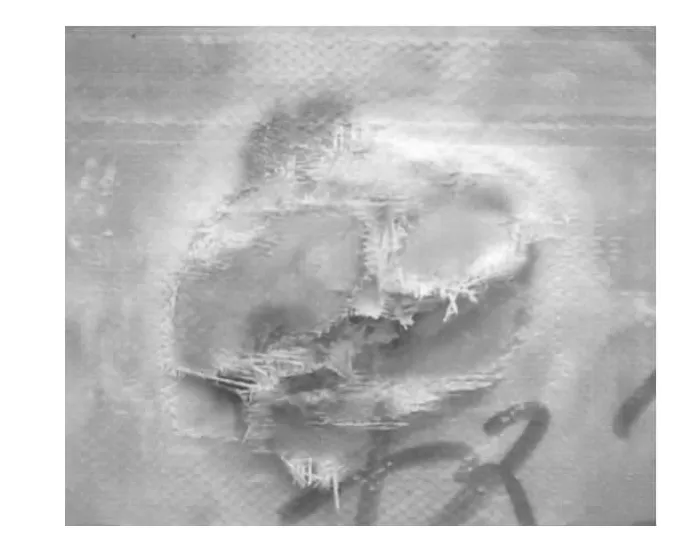
图4 夹芯层背面的破坏Fig.4 Damage of the back of sandwich core

2 理论计算方法

2.1 理论计算的基本假设

基于上面的实验，取图5所示的复合夹芯板为研究对象。夹芯板分为三层，第一层为金属，厚度为S1，密度为ρ1，其中波速为C1;第二层为复合材料，厚度为S2，密度为ρ2，其中波速为C2;第三为金属，厚度为S3，密度为ρ3，其中波速为C3。复合夹芯板的平面尺寸为L×L。

如图6所示，TNT当量为W的炸药在夹芯板附近爆炸时，强烈的爆炸冲击波会迅速作用到夹芯板上。根据炸药的形状和位置，冲击波传播至夹芯板不同位置的时间也不尽相同。但根据前苏联学者的观点［16］，在复杂空间的对称轴附近，可以采用一维波进行分析。即在爆心正对位置处将爆炸冲击波简化成平面波，整个问题也就简化成多层介质中一维平面应变波的传播问题，可以运用一维平面应变波理论进行分析。需要注意的是，这种简化仅适用于对称轴附近，而沿平板面向四周扩展时，需要考虑冲击波的斜入射所带来的影响。

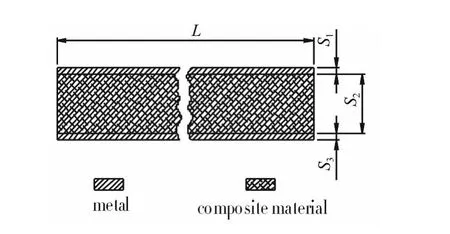
图5 复合夹芯板Fig.5 Composite sandwich plate

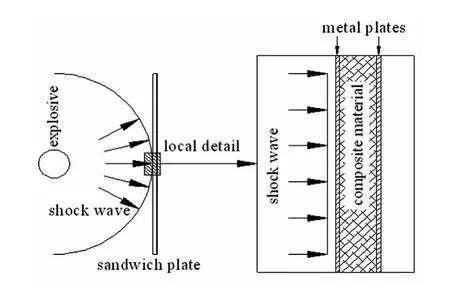
图6 问题简化Fig.6 Simplify of problem

2.2 爆炸冲击荷载

普通炸药空中爆炸时，确定爆炸参数的公式都是根据相似理论建立，其系数则由试验确定，这里引录如下［17］:入射爆炸冲击波超压Δp+的计算公式为式(1)，式中:R—=R/3W m/kg1/3，R为至爆心的距离，W为炸药的TNT当量。爆炸正压作用时间t+如式(2)所示。而爆炸压力变化规律Δp(t)如式(3)所示，其中 n =1

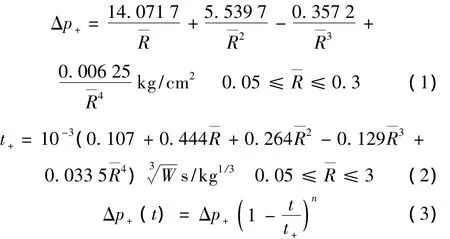
对于空气来说，正反射冲击波超压Δpr的计算公式为式(4)，其正压作用时间与入射波相同，反射压力变化规律如式(5)所示，其中n'=Δpr(n+1)/(2Δp+)-1。

2.3 爆炸冲击波的传播

基本现象:如图7所示，冲击波在夹芯板结构中的传播主要分为二个阶段。第一个阶段(Phase 1)为空气入射冲击波(PAi(t))传入厚度为S1的第一层金属板(metal plate 1)，在金属板的A表面和B表面发生复杂的反射与透射现象，并最终在厚度为S2的复合材料夹芯层中形成透射冲击波(PBt(t))。第二阶段(Phase 2)为复合材料夹芯层中的入射冲击波(PCi(t))传入厚度为S3的第二层金属板(metal plate 2)，在金属板的C表面和D表面发生复杂的反射与透射现象。

图7 冲击波的传播Fig.7 Propagation of shock wave

图7 中的t'代表时间，从冲击波首次到达B界面起算。而T1为冲击波在第一层金属板中传播两倍厚度所需要的时间，所以T1=2S1/C1。同样，T3为冲击波在第二层金属板中传播两倍厚度所需要的时间，且T3=2S3/C3。

第一阶段:空气中爆炸产生的入射冲击波荷载PAi(t)可以用式(3)进行计算，在遇到第一层金属板的A面时会在空气中产生反射冲击波PAr(t)，而在金属板中形成透射冲击波PAt(t)。根据冲击波阵面上力的平衡关系，透射冲击波的压力变化规律可用式(5)进行计算。

假设从A面进入金属板的透射冲击波PAt(t)在t'=0T1时遇到金属板与复合夹芯的交界面B，在B1点发生反射与透射。根据平面波在两种介质间的传播规律，反射系数为FAB=(1-nAB)/(1+nAB)，透射系数为TAB=2/(1+nAB)。其中，nAB=(ρ1C1)/(ρ2C2)为第一层金属板和复合夹芯的波阻抗比。由于nAB＞1，所以FAB＜0，即入射的压缩波反射为拉伸波。此时从B面透射入得合夹芯中的应力波的计算表达式为:

在t'=0.5T1时，从B面反射回来的冲击波在A面上会发生反射，由于空气的波阻抗相对第一层金属板来说可以忽略不计，因此该反射可以考虑为全反射，反射系数为FBA=1，透射系数TBA=0。即拉伸波反射为强度相同的压缩波。

在t'=T1时，从A面反射来的压缩波会再次传播至B面，在B面上发生反射和透射，其反射和透射系数仍为FAB和TAB。那么此时从B面进入复合夹芯的应力波为两次透射波的叠加，其计算表达式为:

依据相同的规律，可以推得在t'=nT1时，从B面进入复合夹芯的应力波为n次透射波的叠加，其计算表达式为:

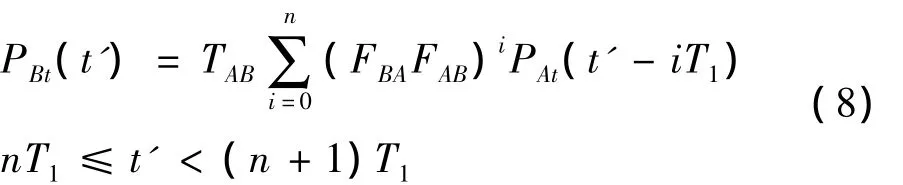
需要注意的是，上述计算公式只在从C面反射回的冲击波PCr(t)到达B面以前成立。

第二阶段:从B面透射过来的透射波PBt(t)通过复合夹芯后形成入射波PCi(t)，不考虑复合夹芯中的衰减，则有PBt(t)=PCi(t)。PCi(t)在C面上发生反射和透射，形成反射波PCr(t)，并在钢板2中形成透射波PCt(t)。

设t″=0T3时PCi(t)到达 C面，与上节类似有，反射系数为FBC=(1-nBC)/(1+nBC)，透射系数为TBC=2/(1+nBC)。其中，nAB=(ρ2C2)/(ρ3C3)为复合夹芯和第二层金属板的波阻抗比。由于nBC＜1，所以FBC＞0，即入射的压缩波反射后仍为压缩波，此后反射波的表达式如下:

在t″=0.5T3时，从C面透射过来的冲击波在D面上会发生反射，由于空气的波阻抗相对钢板来说可以忽略不计，因此该反射可以考虑为全反射，反射系数为FCD=-1，透射系数TCD=0。即压缩波反射为强度相同的拉伸波。

在t″=T3时，从D面反射来的拉伸波会再次传播至C面，在C面上发生反射和透射。其反射和透射系数为FDC=(1-nDC)/(1+nDC)，透射系数为 TDC=2/(1+nDC)。其中 nDC=(ρ3C3)/(ρ2C2)，为第二层金属板和复合夹芯的波阻抗比。那么此后从C面向左传播的应力波应为初次反射波和从D面传入的透射波的叠加，其计算表达式如下:

在t″=2T3时，从D面反射回的应力波会再次到达C面，此后从C面向左传播的应力波应为初次反射波和两个从D面传播的透射波的叠加，其计算公式为:

依据相同的规律，可以推得在t″=nT3后，从C面向左传播的应力波叠加的计算表达式为:

根据C界面上力的平衡条件，C界面上压力应为左传波的压力和入射波压力之和，其计算公式为:

需要注意的是，由于C界面不能承受拉应力，即要求C界面上压力 PC(t″)＞0。假设 PC(tce)=0，则当 t″=tce时C界面两侧材料分离，冲击波传播有第二阶段结束。

2.4 夹芯板的瞬态响应

在爆炸冲击波的作用下，夹芯板的瞬时响应主要体现为结构运动状态以及变形与破坏。下面分别分析各层平板的瞬态响应特性。

第一层金属板:从t'=-S1/C1开始，第一层金属板即受到如式(5)所示的冲击荷载作用，而从t'=0开始，如式(8)所示的冲击波开始通过第一层金属板作用到夹芯层上。那么根据动量守恒定律，即可导出第一层金属板的整体速度变化的计算公式:

其中:m1=ρ1S1为第一层金属板的面密度。在从C界面上反射回的应力波到达B界面以前，上式成立，即要求-S1/C1＜t'＜2S2/C2。

第二层金属板:当t″=tce时C界面两侧材料分离，根据动量守恒定律，第二层金属板分离时获得的动量等于分离前C界面上压力的时间积分，即有

其中:m3=ρ3S3是第二层金属板的面密度，υ3为钢板的分离速度。则第二层钢板的分离速度计算公式为:

夹芯层:在夹芯层中的传播应力波有入射波PCi(t)和反射波PCr(t)，PCi(t)的计算表达式为式(8)，而PCr(t)的计算表达式较为复杂。当t″＜tce时，PCr(t)的表达式为式(12)，而当t″≥tce时，第二层金属板与夹芯层分离，PCi(t)在C界面上发生全反射。因此夹芯层中距离C面x处的压力时程PCx(tx)可以表示为式(17)，其中tx从PBt到达位置x处时起算。

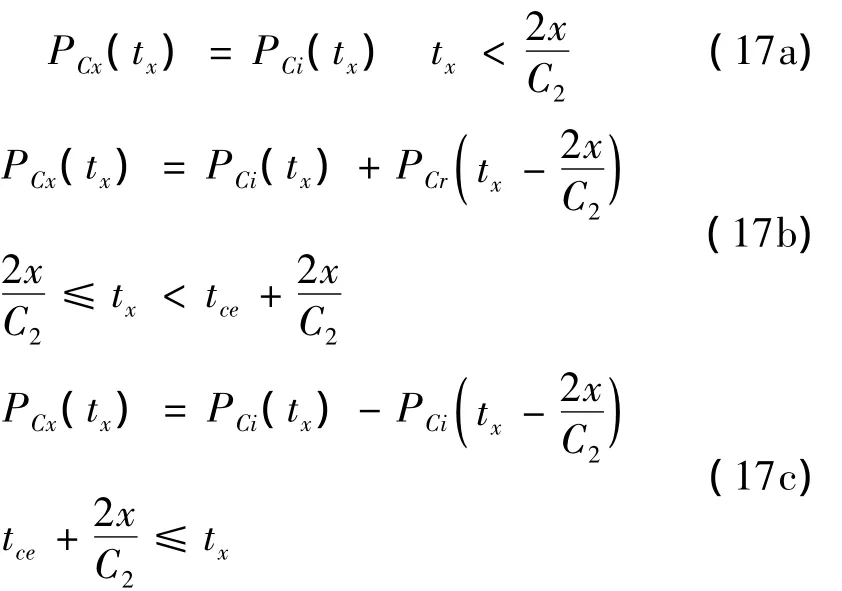
采用较为简单的第一强度理论，当PCx(tx)达到材料的最大拉应力，夹芯层即发生破坏。仔细分析式(17)后可以发现，式(17a)恒大于0，即夹芯层处于受压状态。对于非接触爆炸来说，由于荷载强度的原因，夹芯层很难在受压状态下破坏，因此对于这种情况暂不进行研究。而式(17b)代表的是一个先上升后下降的压力时程，同时式(17c)为一个线性递增函数。所以式(17)的最小值(即最大拉应力)发生在txs=tce+2x/C2时。如果此时的拉应力达到材料的最大拉应力σs，则发生剥落破坏，形成新的自由面。设第一次剥落发生于距离C界面 x1处，即有 PCx1(tx1)= σs，其中 txs1=tce+2x1/C2。此后入射冲击波在新界面x1处继续发生全反射，同样根据最大拉应力强度准则即可判断新破坏面的发生。以上关于夹芯层的破坏分析均未考虑C界面左传波在B界面上的反射，因此需满足txs1＜2S2/C2。

3 算例对比分析

3.1 理论结果

以试验工况为研究对象进行理论计算，计算涉及的部分参数及其取值如表1所示。

爆炸冲击波的传播:忽略装药形状的影响，计算当量为0.4 kg的TNT距离结构R=0.213 62 m的爆炸冲击波荷载。根据式(1)～(5)可得比例距离R—=0.29，入射超压Δp+=107Pa，正压作用时间 t+=0.255 ms，由此可得入射冲击波压力时程如图8所示。而反射超压Δpr=7.66×107Pa，得到的夹芯板前反射超压时程如图9所示。

表1 参数意义与取值Tab.1 Signification and value of parameters

图8 入射冲击波压力时程Fig.8 Pressure time-history of incident shock wave

图9 反射超压时程Fig.9 Pressure time-history in front of sandwich plate

图10 B界面透射冲击压力时程Fig.10 Pressure time-history of transmission shock wave from the interface B

通过式(8)进行计算，从B界面透射入玻璃钢中的波形如图10的间断曲线所示。从中可以看出，连续的冲击波透射入玻璃钢中后成为多次阶跃的非连续波。但从整体上来说，仍可看成具有一定升压时间的冲击波荷载。与图9对比可看出，应力波峰值下降了一半左右，可见界面B对于冲击波具有明显的衰减作用。结合式(8)可以看出，衰减作用的大小与界面B左右的波阻抗比nAB以及第一层钢板的厚度S1成正比。

为方便后续的分析，简化B界面透射冲击荷载。对图10中由各分段波形的中点组成的离散点数据进行双指数函数拟合［18］，得到简化透射冲击波荷载为式(18)，其图形为图10中的连续曲线。

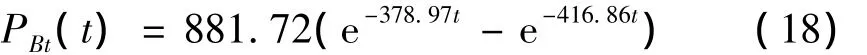
根据表1中的参数，以式(18)为从B界面透射至C界面的波形，代入式(10)和式(13)后，可以得到从C面向左传播的应力波形如图11所示。根据式(14)则可以得到C界面上的压力时程如图12所示。当t″=tce=0.004 4 ms时有PC(tce)=0，即C 界面上压力为0，此后C界面两侧材料分离。

图11 C界面向左传播冲击波压力时程Fig.11 Pressure time-history of left-propagate shock wave from the interface C

图12 C界面上压力时程Fig.12 Pressure time-history on the interface C

图13 钢板的平均运动速度Fig.13 The average velocity of the steel plates

夹芯板的瞬态响应:夹芯板各部分的瞬态响应是研究的重点，基于理论研究可以分别进行计算。首先计算第一层金属板的瞬态响应，根据式(14)得到的第一层金属板整体速度的变化曲线如图13中虚线所示。从中可以看出，第一层钢板的速度开始迅速增加，在t'=0.002 ms时平均运动速度达到最大值8.54 m/s。然后下降，在C界面反射波到达B面时速度降至2 m/s。在这之后受左传波的影响，其速度将进一步下降。

然后计算第二层钢板的瞬态响应。根据表1中的材料参数，可得 m3=ρ1S3=7.86 kg/m3，代入式(16)中即可算得υ3=11.36 m/s。实际上将式(16)中的 tce替换成t，即为第二层钢板的平均运动速度函数，据此画出的图形为图13中的实线。图中第二层钢板的平均运动速度持续增加，在t″=0.004 4 ms时第二层钢板与夹芯层分离并达到最大速度υ3。

最后计算夹芯层的瞬态响应。由于试验采用的玻璃钢由增强材料(高强度玻璃纤维布)和基体材料(3201#乙烯酯树脂)叠加铺成，所以垂直于叠层方向的破坏应由增强材料与基体材料的粘结强度决定。根据试验测得的数据，玻璃钢中增强材料与基体材料的粘结强度为9.5 ～11.2 MPa［19］，现取玻璃钢叠层方向拉伸破坏强度σs=10 MPa，分析玻璃钢夹芯的剥落破坏过程。

图14 距C界面X处压力时程曲线Fig.14 Pressure time-history at the distance of x from the interface C

运用式(17)可以计算夹芯层中应力时程，图14即为距C界面0.003 m 处的应力时程曲线，其最大拉应力发生在0.007 4 ms时。这也就证明了txs=tce+2x/C2时距离C界面x处的应力PCx(tx)达到最小值(即达到最大拉应力)的观点，据此也可以得到夹芯层中最大拉应力沿x方向的变化规律如图15所示。由于当 x=0.002 58 m 时PCx(tx)=-σs，所以第一次剥落破坏发生在 0.002 58 m处。而依据文献［16］的观点，剥落破坏的片数 n*=［σ*/σs］，其中，σ*表示波形的幅值，而方括号表示应取分数的整数部份。从图15可以看出σ*＜20 MPa，而σs=10 MPa，所以n*=1，即只会发生一次剥落破坏。

图15 夹芯层的剥落破坏Fig.15 Damage of sandwich core

3.2 对比分析

复合夹芯板对爆炸荷载的瞬态响应主要体现为结构的变形和破坏。对比试验结果与理论计算结果，二者在钢板的整体变形与局部破坏上吻合较好。

整体变形:理论计算得到的第二层钢板整体速度为11.36 m/s，而第一层钢板的整体速度要小于2 m/s。这表明，第二层钢板所吸收的爆炸冲击波能要远大于第一层钢板。而钢板主要依靠塑性变形吸收冲击动能，因此第二层钢板的变形要大于第一层钢板。这与试验的结果非常吻合，验证了理论计算的正确性。从工程防护的角度看，虽然第一层钢板和夹芯层可以显著降低爆炸冲击波的峰值(从70 MPa至30 MPa)，但第二层钢板才是抵御爆炸冲击波的主要部位。增强第二层钢板的强度和刚度应可有效提高夹芯板抗爆抗冲击能力。

局部层裂破坏:夹芯板的局部破坏主要体现为夹芯层的剥落破坏。理论计算得到的剥落厚度为2.58 mm，而试验测得的最大剥落厚度为2.2 mm，考虑到测量误差，理论与试验结果非常接近，可以证实理论计算的准确性。所以在研究夹芯板的抗爆抗冲击问题时，应考虑夹芯层剥落破坏带来的影响。合理选择夹芯材料，提高夹芯层在垂直平板方向的抗拉能力应可避免或减少剥落破坏的发生，增强复合夹芯板的防护能力。

4 结论

本文基于一维平面波理论，研究了复合夹芯板内波的传播与层裂效应。

(1)考虑应力波在夹芯板各层之间的反射和透射，得到了各层介质中压力时程的理论计算公式，建立了一维平面波荷载在夹芯板中传播的理论计算方法。基于动量定律和第一强度理论，得到了夹芯板运动与破坏特征的理论计算公式。

(2)通过理论计算的结果与试验结果的比较分析证明了理论计算方法的正确性。

(3)夹芯板对爆炸荷载防护特性的分析表明，虽然第一层钢板和夹芯层可以显著降低爆炸冲击波的峰值，但第二层钢板才是抵御爆炸冲击波的主要部位，而复合夹芯层的剥落破坏也需重点关注。

(4)增强第二层钢板的强度和整体刚度，提高夹芯层在垂直平板方向的抗拉强度可以增强复合夹芯板的防护能力。

［1］ Dharmasena K P，Wadley H N G，Xue Z Y，et al.Mechanical response of metallic honeycomb sandwich panel structures to high-intensity dynamic loading ［J］.International Journal of Impact Engineering，2008，35(9):1063-1074.

［2］汪 浩，程远胜，刘 均，等.新型矩形蜂窝夹芯夹层加筋圆柱壳抗水下爆炸冲击载荷分析［J］.振动与冲击，2011，30(1):162-166，226.WANG Hao，CHENG Yuan-sheng，LIU Jun，et al.Antishock analysis for new type rectangular honeycomb sandwich stiffened cylindrical shells subjected to underwater explosion shock load ［J］.Journal of Vibration and Shock，2011，30(1):162-166，226.

［3］Pandit M K，Sheikh A H，Singh B N.An improved higher order zigzag theory for the static analysis of laminated sandwich plate with soft core［J］.Finite Elements in Analysis and Design，2008，44(9-10):602-610.

［4］ Vaidya U K，Pillay S，Bartus S，et al.Impact and postimpact vibration response of protective metal foam composite sandwich plates［J］.Materials Science and Engineering:A，2006，428(1-2):59-66.

［5］Bahei-El-Din Y A，Dvorak G J，Fredricksen O J.A blasttolerant sandwich plate design with a ployurea interlayer［J］.International Journal of Solids and Structures，2006，43(25-26):7644-7658.

［6］ Nemat-Nasser S，Kang WJ，McGee JD，et al.Experimental investigation of energy-absorption characteristics of components of sandwich structures［J］.International Journal of Impact Engineering，2007，34(6):1119-1146.

［7］ Liviu L，Terry H，Camarda C J.Geometrically nonlinear theory of initially imperfect sandwich plates and shells incorporating non-classical effects［C］.AIAA/ASME/ASCE/AHS/ASC Structures，Structural Dynamics， and Materials Conference and Exhibit，37th，Salt Lake City，UT，Apr.15-17，1996.

［8］ Terry H，Liviu L，Camarda C J.Postbuckling of anisotropic flat and doubly-curved sandwich panels under complex loading conditions［J］.International Journal of Solids and Structures，1998，35(23):3007-3027.

［9］ Liviu L，Sang-Yong O，Joerg H.Linear and non-linear dynamic response of sandwich panels to blast loading［J］.Composites Part B:Engineering，2004，35(6-8):673-683.

［10］Terry H，Liviu L.Dynamic response of anisotropic sandwich flat panels to explosive pressure pulses［J］.International Journal of Impact Engineering，2005，31(5):607-628.

［11］ Terry H， Liviu L. Dynamic response of doubly-curved anisotropic sandwich panels impacted by blast loadings［J］.International Journal of Solids and Structures， 2007，44(20):6678-6700.

［12］ Terry H.Elastic structural response of anisotropic sandwich plates with a first-order compressible core impacted by a Friedlander-type shock loading ［J］.Composite Structures，2012，94(5):1634-1645.

［13］ KazancıZ.Dynamic response of composite sandwich plates subjected to time-dependent pressure pulses ［J］.International Journal of Non-linear Mechanics，2011，46(5):807-817.

［14］董永香，冯顺山，李学林.爆炸波在硬-软-硬三明治介质中传播特性的数值分析［J］.弹道学报，2007，19(1):59-63.DONG Yong-xiang， FENG Shun-shan， LI Xue-lin.Numerical analysis of propagation characteristics of explosive wave in the hard-soft-hard sandwich media［J］.Journal of Ballistics，2007，19(1):59-63.

［15］石少卿，刘仁辉，汪 敏.钢板-泡沫铝-钢板新型复合结构降低爆炸冲击波性能研究［J］.振动与冲击，2008，27(4):143-146.SHI Shao-qin， LIU Ren-hui， WANG min. Shock wave reduction behavior of a new compound strueture composed of a foam aluminum layer between two steel plates［J］.Journal of Vibration and Shock，2008，27(4):143-146.

［16］尼基福罗夫斯基 ΒС，舍马金ЕИ.固体动力破碎［M］.余 静，彭庆霁.北京:煤炭工业出版社，1985.

［17］钱七虎.防护结构计算原理［M］.南京:工程兵工程学院出版社，1981.

［18］毛从光，郭晓强，周 辉，等.高空核电磁脉冲模拟波形的双指数函数拟合法［J］.强激光与粒子束，2004，16(3):336-340.MAO Cong-guang，GUO Xiao-qiang，ZHOU Hui，et al.Fitting method of the simulated HEMP waveform by the double-exponential function ［J］.High Power Laser and Particle Beams，2004，16(3):336-340.

［19］陈 昕.雷达防弹天线罩机理研究［D］.武汉:海军工程大学，2009:154-155.