虚拟体在弹炮耦合系统动力学模型中的应用
2013-05-24陈世业王良明
陈世业,王良明,史 伟
(1.南京理工大学 能源与动力工程学院,南京 210094;2.中国兵器工业基团051基地,华阴 714200)
在火炮射击过程中,由于弹炮间隙的存在,弹丸前定心部和弹带与身管内壁发生剧烈的接触碰撞,导致身管振动和弹丸运动两者相互耦合作用,形成火炮的起始扰动并影响弹丸出炮口时刻的初始状态,因此研究弹炮间的耦合运动[1-2]对提高火炮的射击精度具有重要的指导意义。
从目前的研究状况来看,身管和弹丸的耦合系统动力学模型主要采用基于多刚体理论的有限段法[3-4]以及基于弹塑性力学和接触碰撞问题的有限元法[5]。由于身管具有较大的长径比,在系统模型中必须考虑其柔性变形,当弹丸在膛内高速运动时,其与身管内壁的间隙在很小的量级范围内,如何在反映身管柔性变形的前提下充分考虑弹炮间的相互作用,是建立系统刚柔耦合模型[6]过程中存在的一个重要问题;同时,运动过程中弹丸和身管的接触区域在随时变化,即柔性体的边界条件不断改变,若将有限元法应用到整个火炮多体动力学模型中,势必大大降低系统的求解效率。
针对上述问题,本文将虚拟体引入到弹炮系统中,提出一种通过虚拟体来传递弹炮间相互作用力的方法,推导了含虚拟体项的系统多体动力学方程,并结合算例与试验结果进行对比验证了该方法的有效性。
1 系统拓扑关系描述
首先引出本文中虚拟体的概念,即假想的无质量无转动惯量的刚性体,在动力学仿真模型中可以通过把刚体的质量和转动惯量设为极小值来代替。
含虚拟体的弹炮系统拓扑关系如图1所示,h代表部件间的连接关系,图中的柔性身管采用模态法[7-8]来描述其柔性变形,即将事先经过有限元模态解析的身管单元代入系统模型,通过模态振型的叠加来获得对应的应力和应变。
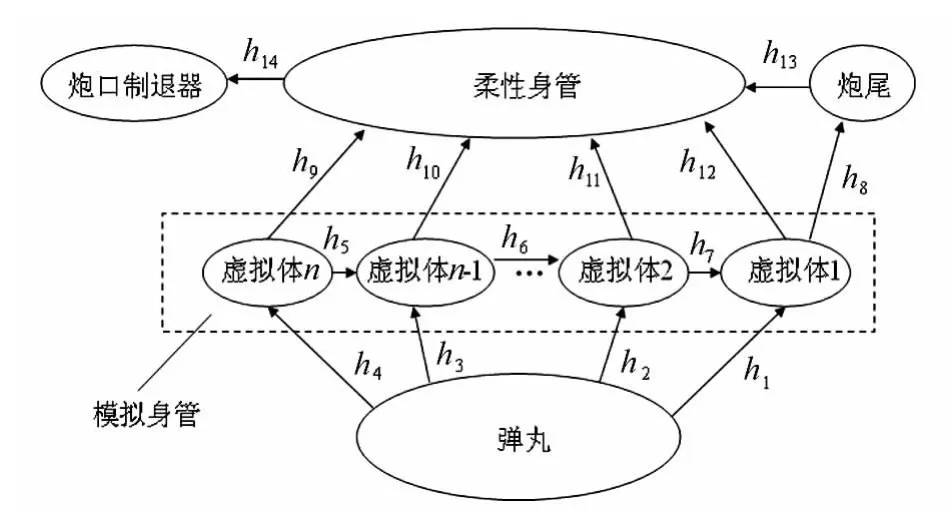
图1 含虚拟体的弹炮系统拓扑关系图Fig.1Topological relation of the projectile-barrel system
模型具体描述如下:由有限个虚拟体组成模拟身管,其中模拟身管的几何模型对应于真实身管的实体外形,虚拟体两端以球铰(h9~h12)形式联接在经过模态解析的柔性身管单元上,相邻虚拟体间以扭转弹簧力(h5~h8)限制其绕身管轴线方向的相对转动,弹丸与虚拟体间的接触碰撞力(h1~h4)通过虚拟体传递到柔性身管单元上并反馈给弹丸运动,柔性身管两端分别与炮尾和炮口制退器固连(h13~h14)。
虚拟体的引入使弹炮间的力元经由模拟身管来间接传递,并将柔性身管和弹丸的耦合作用转化为弹丸与虚拟体间的接触碰撞,实现了弹丸和柔性身管的等效接触,同时有效避免了柔性身管边界条件发生改变这一问题。
2 柔性身管和虚拟体间的运动学方程
在此先列出柔性身管和虚拟体间的运动学约束方程。沿身管轴线方向取任意虚拟体 j,如图2所示,OXYZ为系统的惯性参考坐标系,OmXmYmZm、OjXjYjZj分别为柔性身管m和虚拟体j的连体坐标系,坐标原点均设在对应物体质心处。

图2 身管和虚拟体间的约束Fig.2 Constraint between the barrel and virtual substance
则虚拟体j的坐标原点可以表示为:

同时,虚拟体j的姿态方程由下式确定:

联立式(1)和式(2),即得到柔性身管和任意虚拟体j的运动约束方程:
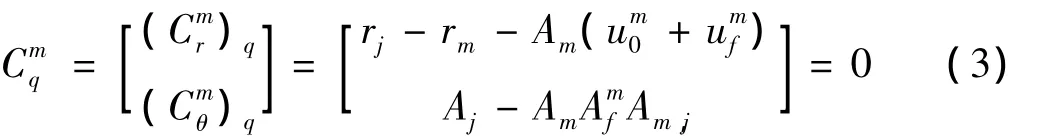

3 含虚拟体的弹炮系统动力学方程
对于任意受约束多体系统中的第i个柔性体或刚体,其对应的动力学控制方程为:

式中:T为动能,qi为广义坐标,λ为拉格朗日乘子,Fi为广义力,为对应的运动约束矩阵。
将构件的动能表达式代入上式并化简可得:

将系统中所有构件产生的运动方程与构件间的约束方程联立,其中,虚拟体与身管间的约束见上节式(3),即构成了含虚拟体的弹炮耦合系统动力学方程:

对于该系统,
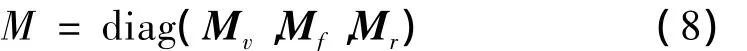
式中:Mv为n个虚拟构件的质量矩阵,刚性构件的质量矩阵Mr包含了弹丸,炮尾和炮口制退器三部分,对应的表达式如下:

柔性身管的质量矩阵Mf为:
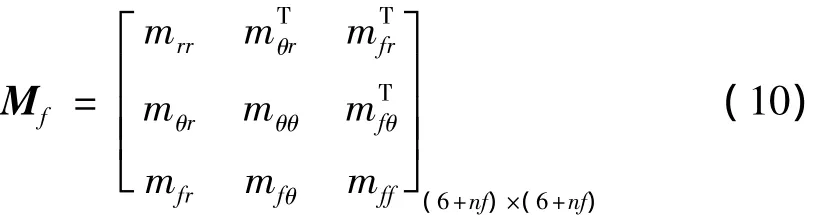
式中:nf为模态坐标的个数。
4 弹丸与虚拟体间的接触碰撞力模型
在刚柔耦合多体系统中,由于需要考虑到柔性体的形变,多采用基于惩罚函数的接触力计算方法,即将接触和碰撞现象按连续的动力学问题来处理。
当弹丸在模拟身管中运动时,如图3所示,考虑弹带和弹丸前定心部与虚拟体间的接触碰撞,基于惩罚函数定义接触力Fn的计算公式为:
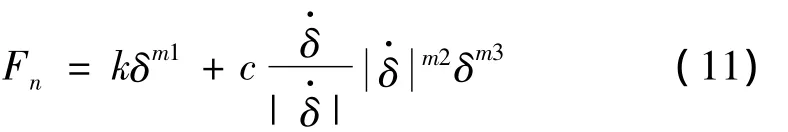
其中:k为接触刚度系数,c为阻尼系数,δ为穿透深度,m1、m2和m3分别为刚度指数、阻尼指数和凹痕指数,则切向摩擦力Ft由下面两个方程确定:

式中:μ和Fmax分别为摩擦系数和定义的最大摩擦力。
综上可知,当弹丸在模拟身管中与虚拟体发生接触碰撞,两者产生的接触力将以广义力Fe的形式传递到系统的动力学方程中,从而对身管的振动造成影响并反馈给弹丸运动。

图3 含虚拟体的弹炮系统模型Fig.3 The projectile-barrel system model including virtual substances
5 算例分析
以某型火炮为例,引入含虚拟体的弹炮耦合模型,如图3所示,模型中由11个虚拟体组成模拟身管,附加了22个柔性铰和11个刚性铰约束,含模态信息的柔性身管单元在炮闩前端面中心处与炮尾固连。
该型火炮某次试验条件为:高低射角0 mil,方向射角0 mil,采用全装药底凹榴弹在常温下射击。将试验条件代入含虚拟体的弹炮刚柔耦合动力学仿真模型,赋予系统初始射角,分别在弹丸底部和炮尾前端面中心处施加火药燃气作用力;同时,取弹丸质量m=21.5 kg,质量偏心为0.15 mm,前定心部与虚拟体内壁的间隙e=0.25 mm,弹带与虚拟体紧密接触,接触刚度k=80 000 N/mm。
系统坐标系定义如下:以炮闩前端面和身管轴线的交点为坐标原点,沿身管轴线指向炮尾后端面为x轴正方向,y轴竖直向下,z轴由右手定则确定。系统模型在经过静平衡分析后在t=0.1 s时开始仿真射击,图4、图5分别给出了身管在后坐运动过程中其后坐位移l和后坐速度v的对比情况。
由图中可以看出,计算结果和实测的火炮后坐运动规律基本相符,炮尾相对于摇架大约在弹丸发射后0.6 s复进到位。
在实际射击过程中,弹丸在膛内运动时将绕身管轴线(x轴)方向加速旋转,在仿真模型中,通过对弹带添加沿x轴的旋转力矩来实现膛线对弹丸的扭转作用。图6、图7分别给出了在x方向上弹丸线速度vd和角速度ωx的计算曲线,由图中看出速度曲线在t=0.112 s左右即不再上升,可知,弹丸从开始发射到离开模拟身管大约经过了12 ms。

图4 后坐位移曲线Fig.4 The curves of recoil displacements

图5 后坐速度曲线Fig.5 The curves of recoil velocities
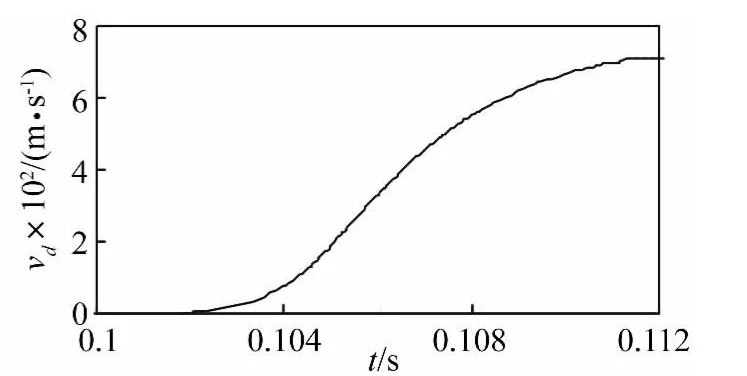
图6 弹丸速度计算曲线Fig.6 The calculated curves of ballet speed
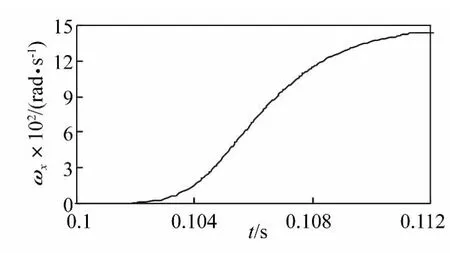
图7 弹丸x方向角速度计算曲线Fig.7 The calculated curves of ballet angular speed in x direction

图8 弹丸y、z方向角速度Fig.8 The ballet angular speeds in y and z directions
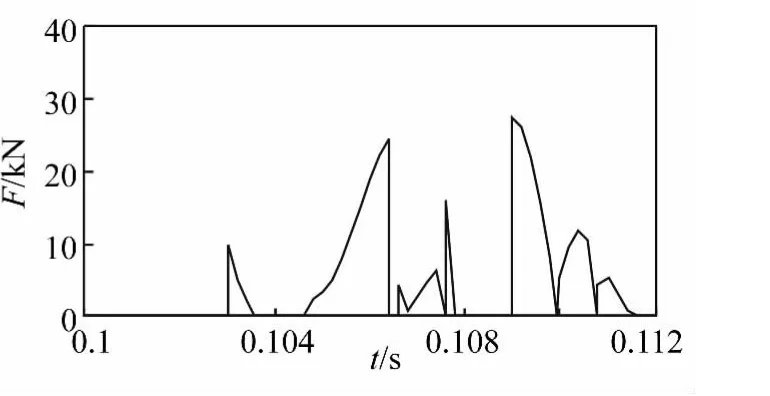
图9 弹丸前定心部和模拟身管间的接触力Fig.9 The contact force between analog barrel and bourrelet
由于试验测得的为弹丸出炮口后在空中飞行的速度曲线,在此取弹丸出炮口时刻的测试值与该时刻对应的计算值进行对比;同时,列出后坐运动的特征参数对比情况。综上,计算值和测试值的相对误差如表1所示,可知将虚拟体应用到弹炮耦合系统模型中,能较真实地反映身管后坐特性和弹丸的膛内运动规律。
图8给出了弹丸在y、z方向的角速度计算结果,可知,由于弹丸前定心部和虚拟体内壁存在间隙,且弹带和虚拟体紧密结合,弹丸在模拟身管中高速运动的同时将绕弹带做俯仰和侧摆运动。
图9和图10分别给出了弹丸前定心部和弹带与模拟身管间的接触力曲线。从图9中可以看出,弹丸围绕弹带中心做角运动时,将不定时与虚拟体内壁发生剧烈的碰撞,形成较大的冲击载荷并作用在模拟身管上;由图10可得,弹带与虚拟体内壁间为紧密配合,两者的作用力主要表现为沿弹带径向的挤压力,且在弹丸的膛内运动过程中始终存在。

表1 计算值和测试值的相对误差Tab.1 The relative errors between the calculation and the test value

图10 弹带和模拟身管间的接触力Fig.10 The contact force between analog barrel and band
6 结论
本文通过将虚拟体引入弹炮系统,推导了柔性身管和虚拟体间的运动约束方程以及含虚拟体的弹炮系统动力学方程,为建立含虚拟体的弹炮耦合系统动力学模型提供了理论基础;同时,以某型火炮为例,通过仿真计算和试验数据的对比,得到如下结论:
(1)基于虚拟体构建弹炮系统模型在理论上是可行的,通过模拟身管来传递弹炮间的力元,实现了柔性身管和弹丸的等效接触。
(2)采用该方法建立的模型能较真实地反映弹丸的膛内运动规律;同时,由于模型中保留了柔性身管的模态信息,故能精确描述身管在外力作用下的振动特性,可以为弹炮耦合问题的研究提供一定参考。
[1]刘 宁,杨国来.弹管横向碰撞对身管动力响应的影响[J].弹道学报,2010,22(2):67-70.LIU Ning,YANG Guo-lai.Effect of lateral impact between projectile and barrel on dynamic response of tube[J].Journal of Ballistics,2010,22(2):67 -70.
[2]苏忠亭,徐 达,李晓伟,等.小口径火炮弹炮耦合动态响应有限元时程分析[J].振动与冲击,2012,31(23):104-108.SU Zhong-ting,XU Da,Li Xiao-wei,et al.Finite-element time-history analysis for dynamic response of small-caliber guns with projectile-barrel coupling[J].Journal of Vibration and Shock,2012,31(23):104-108.
[3]刘 雷.弹丸-身管耦合系统动力学模型[J].振动与冲击,2007,26(6):121 -124.LIU Lei.Dynamic model of the projectile-barrel compuling system[J].Journal of Vibration and Shock,2007,26(6):121-124.
[4]刘 雷,陈运生,杨国来.基于接触模型的弹炮耦合问题研究[J].兵工学报,2006,27(6):984-987.LIU Lei,CHEN Yun-sheng,YANG Guo-lai.A study on the projectile-barrel coupling based on contact model[J].Acta Armamentarii,2006,27(6):984 -987.
[5]葛建立,杨国来,陈运生,等.基于弹塑性接触/碰撞模型的弹炮耦合问题研究[J].弹道学报,2008,20(3):103-106.GE Jian-li,YANG Guo-lai,CHEN Yun-sheng,et al.A study on projectile-barrel coupling problem based on elastoplastic impact model[J].Journal of Ballistics,2008,20(3):103 -106.
[6]徐航手,刘铸永.刚柔耦合动力学的建模方法[J].上海交通大学学报,2008,42(11):1922-1926.XU Hang-shou,LIU Zhu-yong.Modeling methods of rigidflexible coupling dynamics[J].Journal of Shanghai Jiaotong University,2008,42(11):1922-1926.
[7]史跃东,王德石.舰炮振动的刚柔耦合动力学分析[J].弹道学报,2010,22(1):37 -39,44.SHI Yue-dong,WANGDe-shi.Vibration analysis of naval gun by rigid-flexible coupling dynamics[J].Journal of Ballistics,2010,22(1):37 -39,44.
[8]苏忠亭,徐 达,杨明华,等.基于模态试验的某火炮身管有限元模型修正[J].振动与冲击,2012,31(24):54-59.SU Zhong-ting,XU Da,YANG Ming-hua,et al.Finiteelement model updating for a gun barrel based on modal test[J].Journal of Vibration and Shock,2012,31(24):54-59.
