可重图的Randić指标的极值问题

胡玉梅(天津大学理学院，天津 300072)

可重图的Randić指标的极值问题

胡玉梅
(天津大学理学院，天津 300072)

图G的Randić指数，χ(G)，是分子图的一种拓扑指标，它的值可以反映分子的许多物理化学性质．在化学分子中双键是普遍存在的．为此，研究了恰有一条重边的可重图的Randić指标的极值问题，给出了树图及化学树图的Randić指标的极值及相应的结构．

Randić指标；极值；可重图；树图

一个分子图的拓扑指标值是由分子的结构图计算得到的一个数值，它是图的不变量，一般可以反映分子的物理化学性质和药物学性质．1975年，Randić提出了著名的连通性指标(Randić指标)，因其与分子的物理化学性质，如沸点、表面积等，都有紧密联系，近年来受到化学家和数学家广泛关注，详见参考文献[1-7]．Randić指标的定义为χ(G)=其中du和dv分别表示图G中顶点u和v的度数．

在图论的应用中，分子的化学结构可以很简单地表示成图的形式，这样的图也称为化学图，或者分子图．在化学中分子图中经常遇到多键，如甲醛和乙烯等．如果用可重边来表示多键的话，那么就会得到一个可重图．而目前在研究分子图的拓扑指标问题的文献中，多数只研究简单图．所以有必要研究在可重图中拓扑指标的极值问题．

设G(m，n)表示有n个顶点、m条边的可重图(存在重边但没有环)．如果一个可重图基本的简单图没有圈，称为可重树．称一个图为化学图，其最大度不超过4．简便起见，笔者称“恰有一条重边的可重(化学)树”为“1-重(化学)树”．类似的，“1-重路”Pn1表示其基本简单图是路的可重树，且唯一的重边位于路的一端；“1-重星”Sn1是一个基本简单图为星的多重树．

在分子图的拓扑指标领域一个很重要的问题就是对于给定图类的指标的极值以及达到极值时相应图的结构．早期研究表明在n个顶点的树中，路图具有最大的Randić指标值，而星图有最小值．Gutman等[8-9]用线性规划的方法给出了n个顶点的简单化学树的最大和最小Randić指标值．笔者研究恰有一条重边的n个顶点的可重图．首先使用线性规划方法给出了n个顶点的1-重化学树的最大和最小Randić指标值．其次，证明了在所有1-重树中1-重星具有最小的Randić指标．最后，用Caporossi等[10]的研究方法证明在所有1-重树中1-重路具有最大的Randić指标．

1 具有最大和最小Randić指标的1-重化学树

在可重图G(m，n)中，记ni表示i度点的个数；称一边为ij边，如果其端点分别为i度点和j度点，记xij表示ij边的个数．则有整数线性规划模型

应用单纯形算法，并设m=n．

若取1n、2n、3n、4n、12x、22x为基变量，可得

所有的系数cij都是负值，所以为使χ(G)达到最大值，须有n3和n4的取值尽量小．

定理1.1 若T是有n个顶点的1-重化学树，则

证明：假设G*是具有最大Randic指标值的1-重化学树，即χ(G*)≥χ(Pn1)．因为在1-重化学树中至少有1个顶点其度大于等于3，则n3+n4≥1．

若在G*中有341nn+＞，则由式(5)和式(6)，得

因为cij＜0，则

与G*的定义矛盾．

若在G*中有n3=0，n4=1，则由式(6)得

证毕．

类似地考虑最小值问题，可以得到下面的定理．证明从略．

定理1.2

(1) 若n≡0(mod3)，则在所有n个顶点1-重化学树中，没有2度和3度点(也就是说只有度为1和4的顶点)的树，记为L1，具有最小的Randić指标值．

(2) 若n≡1(mod3)，则在所有n个顶点1-重化学树中，没有3度点，且只有1个2度点与1个4度点相邻，二者与唯一的重边相关联的树，记为L2，具有最小的Randić指标值

(3) 若n≡2(mod3)，则在所有n个顶点1-重化学树中，没有2度点，只有1个3度点与2个4度点相邻，且与唯一的重边相关联的树，记为L3，具有最小的Randić指标值

2 具有最小Randić指标值的1-重树

记T*为n个顶点的具有最小Randić指标值的1-重树．称(dudv)-1/2为边uv的权重．

引理2.1 设u为T*的一个1度点，v是u的邻点，则T*中至少存在2条与v相关联的边，其权重不超过(2dv)-1/2．

证明：用反证法，假设结论不成立．则T*中v的邻点，除点s外，都是1度点，且边sv不是重边．将边sv收缩至一点w，且添加一个新的叶子点与w相邻，得到一个新的1-重树，记为T′．设xj为除v外s的邻点，j=1，2，…，ds-1．记ds=x≥2,dv=y ≥2，有

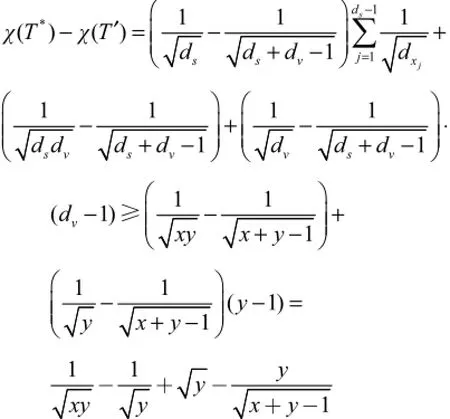
将最后一个等式记为(,)fxy，因为当2x≥、

用归纳法，容易验证当n=4，5时不等式成立．下面假设n≥6且等式对所有顶点数小于n的1-重树都成立．

设u为T*的一个1度点，v是u的邻点，wi(i= 1，2，…，dv-1)是v的除顶点u以外的其他邻点．显然有dwi≥1，由引理2.1，有

因为vdn≤，则

由此定理结论成立．证毕．

3 具有最大Randić指标值的1-重树

首先区别2种类型的边：对称边和非对称边．一条边称为对称边，如果它的2个端点具有相同的度；否则称为非对称边．

Caporossi[10]等得到简单图中Randić指标的另一种表示形式．不难验证，这一结果也适用于1-重图．所以有以下引理．

引理3.1[10]设G为既无孤立点也无环的1-重图，则Randić指标可以重新表示为

由上式可见，对称边的权重为0，而非对称边的权重为正数．

定理 3.2 在所有n个顶点1-重树中，“1-重路”Pn1具有最大的Randić指标值．证明：注意到树图中必定存在的悬挂边就是非对称边．特别的，在1-重树中至少存在一个度大于等于3的顶点．为使χ(G)达到最大值，须有非对称边的数目尽量少，且非对称边的权重尽可能小．如果存在某1-重树恰好同时满足下列3个条件：

(1) 具有最少的悬挂边数(=2)；

(2) 在非悬挂边中，具有最少的非对称边数(=1)；

(3) 非对称边的权重尽量小．

则这个树就具有最大的Randić指标值．容易验证，1-重路p1n满足上述条件的唯一的1-重树．得证．

4 结 论

(1) 对于n个顶点的1-重化学树，“1-重路”Pn1具有最大的Randić指标值；且具有最小的Randić指标值的1-重化学树的结构已给出．

(2) 对于n个顶点1-重树，“1-重星”Sn1具有最小的Randić指标值；“1-重路”Pn1具有最大的Randić指标值．

［1］ Li Xueliang，Gutman I. Mathematical Aspects of Randić-Type Molecular Structure Descriptors，Mathematical Chemistry Monographs No. 1 [M]. Kragujevac：University of Kragujevac and Faculty of Science Kragujevac，2006.

［2］ Li Xueliang，Shi Yongtong．A survey on the Randić index[J]. MATCH Commun Math Comput Chem，2008，59(1)：127-156.

［3］ Shiu Wai Chee，Zhang Lianzhu．The maximum Randić index of chemical trees with k pendants [J]. Discrete Mathematics，2009，309(13)：4409-4416.

［4］ You Zhifu，Liu Bolian．On a conjecture of the Randić index[J]. Discrete Appl Math，2009，157(8)：1766-1772.

［5］ Fischermann M，Hoffmann A，Rautenbach D，et al. A linear programming approach to the generalized Randić index [J]. Discrete Appl Math，2003，128(2)：375-385.

［6］ Delorme C，Favaron O，Rautenbach D. On the Randić index [J]. Discrete Math，2002，257(1)：29-38.

［7］ Caporossi G，Gutman I，Hansen P. Variable neighborhood search for extremal graphs IV：Chemical trees with extremal connectivity index [J]. Computers and Chemistry，1999，23(5)：469-477.

［8］ Gutman I，Araujo O，Morales D A. Bounds for the Randić connectivity index [J]. J Chem Inf Comput Sci，2000，40(3)：593-598.

［9］ Gutman I，Miljkovic O，Alkanes C G，et al. Alkanes with small and large Randić connectivity indices [J]. Chemical Physics Letters，1999，306(5)：366-372.

［10］ Caporossi G，Gutman I，Hansen P，et al. Graphs with maximum connectivity index [J]. Comput Biol Chem，2003，27(1)：85-90.

Multigraphs with Extremal Randić Indices

Hu Yumei
(School of Sciences，Tianjin University，Tianjin 300072，China)

χ(G), the Randić index of G, is a proposed molecular descriptor, and is well correlated with a variety of physico-chemical properties of alkanes. Since multiple bonds are often encountered in molecular graph in chemistry. The purpose of this paper is to derive the extreme values of Randić index for molecular graph with exactly one multiple bond. The definitions of 1-multitree and chemical 1-multitree are given. Then the extreme values of Randić index for 1-multitree and chemical 1-multitree are obtained, respectively. And the corresponding structures are also discussed.

Randić index；extremum；multigraph；tree

O157

A

0493-2137(2013)03-0281-04

2011-05-19；

2011-09-26.

国家自然科学基金资助项目(11001196).

胡玉梅（1977— ），女，博士，副教授．

胡玉梅，huyumei@tju.edu.cn.