确定循环荷载作用下吸力锚承载力的塑性上限法
2013-05-23刘晶磊王建华天津大学水利工程仿真与安全国家重点实验室天津300072天津大学岩土工程研究所天津300072
刘晶磊,王建华(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300072;2. 天津大学岩土工程研究所,天津 300072)
确定循环荷载作用下吸力锚承载力的塑性上限法
刘晶磊1,2,王建华1,2
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300072;2. 天津大学岩土工程研究所,天津 300072)
塑性上限分析法是计算静荷载作用下吸力锚极限承载力的一种方法,依据塑性上限分析原理,为了计算静荷载与循环荷载共同作用下吸力锚的承载力,建议了一种基于塑性上限分析理论计算静荷载和循环荷载共同作用下软黏土中张紧式吸力锚循环承载力的方法.该方法首先假定在静荷载作用下吸力锚的破坏模式,并依据静力平衡原理计算静荷载在土体中产生的平均剪应力,然后依据循环强度与土体平均剪应力和循环破坏次数的相互关系确定相应的循环强度,将循环荷载对土体的作用转化成土体强度的变化,再假定吸力锚在循环荷载下的破坏模式与静荷载作用下其破坏模式一致,并依照塑性上限分析原理和土体的循环强度计算强度变化后的承载力.为了验证该方法的合理性,进行了1g条件下的吸力锚模型试验,并应用该方法对模型试验结果进行了预测,预测结果与试验结果吻合较好.
吸力锚;循环承载力;循环强度;塑性上限分析;吸力锚模型试验
随着人类对油气能源需求的日益增加,海洋油气开采逐渐走向深水.深水条件下,锚泊系统由于其经济、安装施工方便的特点,成为深水油气开采广泛应用的基础形式[1].作为海洋浮式平台基础的张紧式吸力锚,其所受荷载包括由上部结构受浮力作用产生的工作荷载,风、波浪以及洋流引起的低频循环荷载,飓风和飓浪产生的高频循环荷载.评价循环荷载作用下黏土中张紧式吸力锚的承载力,是设计张紧式吸力锚的一项重要内容.
目前,评价循环荷载作用下软土地基承载力的主要方法为依据土循环剪切强度的拟静力法.通常,土的循环剪切强度被定义为在一定的循环破坏次数下、土单元达到破坏标准时所需的平均剪应力与循环剪应力之和.文献[2-5]中就建议利用土的循环剪切强度、依据Andersen等[3]提出的拟静力极限平衡分析原理,分析最佳系泊点受静荷载和循环荷载共同作用下黏土中张紧式吸力锚的承载力,然而迄今为止尚鲜见相关分析过程的文献报道.文献[6-7]依据软黏土的不固结不排水循环剪切强度,通过拟静力弹塑性有限元法计算评价软黏土中桶形基础在静荷载与循环荷载共同作用下的承载力,并与模型试验结果进行了对比,结果表明分析结果小于模型试验结果20%左右. 拟静力方法的核心思想是将循环荷载对土体的作用转化成土体强度的改变,并将循环荷载视为拟静力荷载,利用改变后的土体强度(即循环强度)结合适当的分析原理、通过相应的分析过程计算静荷载与拟静力荷载共同作用下地基的承载力,以达到评价地基循环承载力的效果.
基于以上分析,笔者尝试将拟静力分析方法的思想与塑性极限分析原理相结合,探讨通过塑性极限上限分析评价软土中张紧式吸力锚在静荷载与循环荷载共同作用下承载力的方法,并通过1g条件下的模型试验对本文所提方法的可行性进行验证.
1 软黏土的循环剪切强度
对于饱和软黏土,影响其循环剪切强度的主要因素有:循环荷载作用前土体的初始应力状态、循环荷载的大小、作用方式与循环次数.软黏土的循环剪切强度通常理解为在一定的循环破坏次数下,土单元达到破坏标准时所需的平均剪应力与循环剪应力之和[3,8],即

式中:τa为循环荷载作用前土体受到平均剪应力;τcy为循环剪应力.
为了利用循环剪切强度计算循环荷载作用下地基的承载力,通常可以通过土的动力试验确定土的循环剪切强度.对于不固结不排水循环三轴试验,平均剪应力就是循环应力作用前土单元受到的初始剪应力.已有研究表明,循环剪切强度取决于循环破坏次数、平均剪应力以及循环剪应力,通常把土动力试验确定的循环剪切强度表示为相同循环破坏次数下循环剪切强度随平均剪应力的变化关系[9-10].
文献[10-11]通过循环扭剪与循环三轴试验研究了软黏土在不固结不排水条件下的循环强度.研究结果表明,软黏土在不固结不排水条件下的循环剪切强度满足Mises破坏准则,即由循环扭剪试验确定的循环剪切强度τf,cy与循环三轴压缩试验确定的循环压缩强度σf,cy之间的关系满足

式中σf,cy为循环三轴试验测定的循环压缩(拉伸)强度.
在循环三轴试验中,循环压缩(拉伸)强度与土样所受围压无关,且相同循环破坏次数下,三轴压缩试验测定的循环压缩强度与三轴拉伸试验测定的循环拉伸强度是相同的.
通常情况下,软黏土的状态多为正常固结或欠固结状态,考虑到吸力锚的现场安装时间短,安装后便马上投入工作,这里按照偏于安全的情况考虑,依据不固结不排水强度评价吸力锚安装后的稳定性.针对本文模型试验软黏土,进行了不固结不排水条件下的循环三轴压缩试验与循环三轴拉伸试验,试验中给土样施加的围压为30,kPa,这里用σa表示施加循环应力前,土样受到的轴向平均应力(即轴向静偏应力),用σf表示静三轴试验确定的静压缩(拉伸)强度.
为了得到σa对循环压缩(拉伸)强度的影响,分别取σa/σf=0、0.3、0.5、0.7进行试验.图1与图2给出了由试验得出的循环压缩与循环拉伸强度曲线.图中,对于试样破坏形式为循环累积应变的试验,按平均应力与循环应力共同作用下试样轴向静应变与循环累积应变之和达到10%确定循环破坏次数;对于试样破坏形式为循环应变的试验,按平均应力与循环应力共同作用下试样循环应变达到10%确定循环破坏次数.由图1与图2,做出同一循环破坏次数对应的归一化循环压缩(拉伸)强度(循环压缩(拉伸)强度与静强度之比)随归一化平均应力(平均应力与静强度之比)的变化关系,见图3.图3中结果表明,循环三轴压缩与循环三轴拉伸试验得出的同一循环破坏次数下归一化循环压缩、拉伸强度随归一化平均应力的变化关系是一致的,这也进一步说明上述分析的正确性.
参照图3给出的关系,若已知土单元归一化平均应力,就可以确定归一化的循环压缩(拉伸)强度.在循环压缩(拉伸)强度满足Mises破坏准则前提下,就可以依据归一化的循环压缩(拉伸)强度,由任意破坏面上的静强度确定相应的循环剪切强度.

图1 循环三轴压缩试验得到的循环强度曲线Fig.1 Cyclic strength curves from cyclic triaxial compression tests

图2 循环三轴拉伸试验得到的循环强度曲线Fig.2 Cyclic strength curves from cyclic triaxial tension tests

图3 归一化循环强度随归一化平均应力的变化Fig.3 Normalized cyclic strength vs normalized average stress
2 吸力锚极限承载力塑性上限分析法简介
Aubeny等[12-13]对Murff等[14]提出的桩受水平荷载作用时的破坏模式进行了简化,提出了软土中的锚在倾斜荷载作用下的破坏机理与相应的破坏模式,见图4.这个破坏模式假设锚在倾斜荷载作用下绕一转动中心发生转动,且锚底以下部分土体与锚一起转动并形成一个球形区.当转动中心在锚底以下无穷远处时,这个破坏模式就描述了最佳系泊点受荷锚平动的破坏模式.基于此破坏模式,Aubeny提出了分析倾斜荷载作用下吸力锚极限承载力的塑性上限法.

图4 吸力锚刚体运动和速度场Fig.4 Rigid body motions and velocity field of suction anchors
塑性极限分析上限定理指出,由机动许可速度场确定的极限荷载一定不小于真实的极限荷载[15].因此,Aubeny提出的塑性上限分析方法的原理就是在假设的所有机动许可速度场中,寻求与机动可能速度场对应的最小极限荷载,以此逼近真实的极限荷载.按照塑性上限分析法,在给定破坏模式后,需要依据耗散能率原理列出相应的耗散能率方程,进而求解极限荷载.其方程为



式中:D为吸力锚的直径;I1=0.68;I2=15;I3=8;Su1为吸力锚侧壁周围土层的不排水剪切强度;Mb0为锚围绕转动中心发生纯转动时,锚底球型破坏面上剪切强度对锚转动中心的力矩[12-13];Rf为反映泥面处土层极限抗力衰减的系数,其表达式为

式中:N1=9.42+2.52α;N2=7.42+1.70α,α为锚侧壁摩擦阻力与土的剪切强度之比.
Vb0为承受竖向拉拔荷载时,锚底部的反向承载力,其表达式为

式中:Atip为吸力锚底部面积;Su2为吸力锚底以下土层的不排水剪切强度;Nc为反向承载力系数,其值取9.
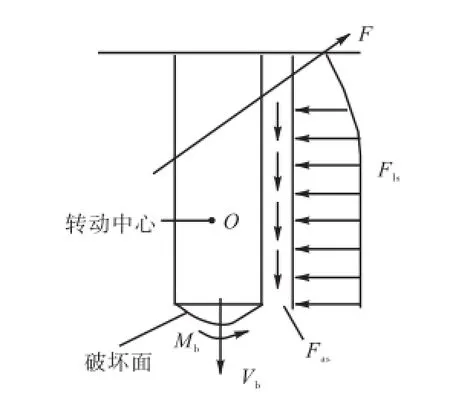
图5 吸力锚在转动过程中的受力分析Fig.5 Stress analysis of suction anchors during rotation
Aubeny将锚的平动速度与转动角速度定义为广义速度.根据塑性上限分析原理,需定义一个机动可能的速度场.设锚侧壁泥面处的水平速度为v0,任意点水平速度为vl,竖直速度为va=ξv0(其中ξ为速度相关系数),锚的转动角速度为β˙=v0/L0.将锚视为刚体,据此构造出的速度场就是一个满足边界条件的机动可能速度场,见图4.于是,W˙、D˙s与D˙b的表达式分别为

将式(8)~式(10)代入式(3)得到耗散能率方程,简化后得外荷载水平分量表达式,即式中:H为外荷载的水平分量;V为外荷载的竖直分量,V=Htan,θ;θ为加载方向与水平向之间夹角;Li为加载点到泥面的距离;L0为转动中心距泥面的距离;Lf为锚的贯入深度.
进一步,假设广义应力与广义速度之间满足相关联的流动法则,由式(4)就可以建立Fls、Fas与广义速度之间的关系,由式(5)就可以建立Vb、Mb与广义速度之间的关系.由于广义速度取决于转动中心位置L0、速度相关系数ξ,故式(11)确定的H也只与L0、ξ有关,且它的最小值与真实的极限荷载接近,故通过优化算法确定式(11)的最小值.
3 吸力锚循环承载力分析方法
下面将分析如何在塑性上限分析方法中利用循环剪切强度分析循环荷载作用下吸力锚的承载力.循环荷载作用前,锚周围与锚底以下土层会受到由于土层k0应力状态和工作张紧力而导致的初始剪应力作用.相对于循环荷载,这个初始剪应力就是循环荷载作用前土单元受到的平均剪应力τa[2-3].当循环荷载作用后,土单元又受到一个循环剪应力τcy的作用.于是,在工作荷载和循环荷载共同作用下,土层单元受到的应力包括平均剪应力τa和循环剪应力τcy.当τa+τcy大于循环剪切强度τf,cy时,土单元发生破坏.
如前所述,循环破坏次数给定后,土单元的循环剪切强度取决于平均剪应力τa,因此确定土单元受到循环荷载前的平均剪应力尤为重要.土单元的位置不同,受到的平均剪应力也不一样,循环剪切强度也就不同.外荷载作用下,锚周围与锚底以下土层单元具有复杂的应力状态,如果在塑性上限分析方法中详细考虑不同位置土层单元上平均剪应力的影响,将使问题变得十分复杂.为此,这里不考虑不同位置土单元平均剪应力的差异,通过引入锚侧壁周围土层的等效平均剪应力与锚底以下土层的等效平均剪应力,考虑平均剪应力对循环强度进而对承载力的影响,且认为等效平均剪应力是由循环荷载作用前锚受到的张紧荷载所引起的.于是,把张紧力产生的静荷载作为已知平均荷载,把需要确定的锚侧壁周围与锚底以下土层单元的等效平均剪应力作为强度,借助静力平衡原理将张紧荷载与土体等效平均剪应力产生的内力平衡,从而确定循环荷载作用前锚周围土层单元与锚底以下土层单元的等效平均剪应力.
由于循环荷载作用方向与静荷载作用方向一致,故假设静荷载与循环荷载共同作用下锚的破坏模式与静荷载作用下的破坏模式一致.利用土层循环剪切强度确定循环荷载作用下吸力锚承载力的步骤如下.
步骤1 依据软黏土层的不排水静剪切强度,通过塑性上限分析法计算锚的静极限承载力Ff.定义NH和NV分别为极限状态时锚侧壁周围土层的水平与竖向承载力系数,假定NH和NV不受锚发生转动的影响,则当锚在最佳系泊点受荷平动时,NH和NV满足

式中:Ff,H为静极限承载力的水平分量;Ff,V为静极限承载力的竖直分量;Vb为任意加载方向锚底以下土体的反向承载力.
联立式(12)和式(13)确定NH和NV.
对Vb做如下分析:模型试验结果显示,当锚的加载方向变化时,锚底以下土体的反向承载力Vb并不是一个常数,故在反向承载力系数中引入一个反映加载方向变化的修正系数ic.首先,利用塑性上限法与极限平衡法[5],确定与试验结果对应的反向承载力系数Nc*,再按ic=Nc*/Nc确定修正系数,进而对同一方向的3个结果取平均值并做出ic随载荷方向θ角的变化关系,见图6.图中,对于θ=0°、90°时的值,按Hansen地基承载力关系,将ic分别取为0.5和1.0.采用多项式拟和曲线得出ic随θ的变化关系,即


图6 ic随θ 变化曲线Fig.6Curve of icvs θ
步骤2 依据Ff,计算预定平均荷载比Fa/Ff对应的平均荷载Fa.
步骤3 假定锚受到平均荷载作用时满足静力极限平衡条件,将锚侧壁周围与锚底以下土层单元的等效平均剪应力作为强度,则由式(12)得

式中:Fa,H为平均荷载的水平分量;τa1为锚侧壁周围土层单元的等效平均剪应力.
由式(13)得
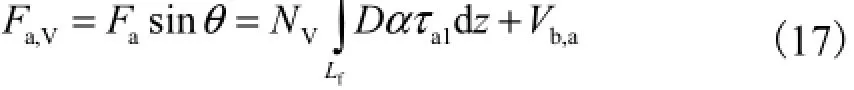
式中:Fa,V为平均荷载的竖向分量;Vb,a为平均荷载作用时,锚底以下土层产生的反向阻力,按以上假设,Vb,a由锚底以下土层的等效平均剪应力τa2确定,则Vb,a=icAtipτa2Nc.
步骤1中确定的NH和NV代入式(16)和式(17),并联立式(16)和式(17)确定锚壁周围土层等效平均剪应力τa1以及锚底以下土层的等效平均剪应力τa2,进而确定锚周围以及锚底以下土层的归一化平均剪应力比τa1/τf和τa2/τf,这里的τf是土层的不固结不排水静剪切强度.
步骤4 依据τa1/τf和τa2/τf,结合土动力试验确定的试样轴向归一化的循环强度比随轴向归一化平均应力比变化的循环强度曲线确定锚周围以及锚底以下土层的循环剪切强度比,由实测的模型试验土层的静强度确定相应的循环剪切强度.
步骤5 假定在循环荷载作用下,除强度以外的其他参数不变,即假设其他参数不受循环荷载影响.将锚壁周围以及锚底以下土层的静剪切强度换为循环强度,利用塑性上限分析法求解静极限承载力的方法计算此时的承载力,该计算结果就是静荷载与循环荷载共同作用下锚的极限承载力,即锚的循环承载力.
4 方法的可行性分析
为了说明上述分析方法的可行性,首先通过1g条件下的模型试验,确定不同静荷载与循环荷载共同作用下吸力锚的承载力,进一步采用上述方法预测模型试验结果并进行对比分析.
4.1 模型试验装置与试验方法
模型试验箱的尺寸为长×宽×高=1.2,m×1.0 m×1.2,m.模型试验土层为天津塘沽滩海淤泥质重塑软黏土.使用真空预压法制备试验土层,制备过程中定期在土层不同位置进行十字板剪切试验,当土层沿深度的不排水强度达到6~8,kPa时,停止对土层抽真空,制备好的土层厚0.9,m,平均含水量42%,天然容重17.88,kN/m3,且十字板剪切试验结果表明土层沿深度的不排水强度分布比较均匀.模型锚为长径比为6的不锈钢圆桶,直径0.076,m,高0.456,m,壁厚0.002,m,表面光滑,通过采用与模型锚相同材料、相同壁厚的平板进行竖向拔出试验,结果表明模型试验所用锚的侧壁摩擦阻力与土的剪切强度之比的平均值为0.055,吸力锚下部敞开,为了便于观察锚贯入过程中锚内土塞变化情况,锚的上部安装了一个密封的有机玻璃上盖,其上设置1个排气孔,通过计算得到模型试验中最优加载点位于锚侧壁距锚顶0.27,m处.
选择不同加载方向、不同静荷载比Fa/Ff进行静荷载与循环荷载共同作用下的承载力模型试验.为了在有限空间的模型试验土池内进行不同加载方向张紧式吸力锚模型试验,制作了可变加载方向、移动方便的模型试验加载导向装置,见图7.该导向装置由加载框架、导向板以及导向滑轮组成,上部导向滑轮的位置固定,试验时只须调节下部导向滑轮在导向板上的位置,便可以实现加载方向的改变.测量传感器位置如图8所示,其中力传感器用于测量锚受到的系泊方向荷载,1号位移传感器用于测量锚受荷点沿加载方向的位移,2号和3号位移传感器用于测量锚的竖向位移,4号位移传感器用于测量锚的水平位移.通过这些测量值便可计算出锚在竖直平面内的转角以及转动中心的位置.试验过程包括静承载力试验与循环承载力试验.
静承载力模型试验过程如下.
(1) 为考虑土层剪切强度随时间变化对试验结果的影响,每次试验前,使用十字板再次测量试验位置处土层强度沿深度的变化.
(2) 由于试验锚的直径较小,故采用负压与重力联合法将锚沉入预定的试验位置土层中,沉锚后静置3,d后进行试验.
(3) 在力控制下,采用分级加荷方法给锚施加静荷载,将随时间变化相对稳定后的位移作为该级荷载作用下的位移.当某级荷载作用下的位移随时间不能趋于稳定时,发生破坏,此时停止试验.
循环承载力模型试验过程如下.
(1) 同上道理,测定试验前土层的强度并将锚贯入.
(2) 采用分级加荷法,按预定的静荷载比Fa/Ff给锚施加静荷载.由于多种客观因素影响,每一次试验的静承载力Ff存在差异.因此为了客观估计每一次试验的静承载力,以多次静承载力模型试验得到的沿系泊方向归一化荷载位移曲线为基准,参照预定的Fa/Ff对应的系泊方向位移估算Ff.
(3) 以预估的Ff为基准,给锚施加0.1,Hz的正弦循环荷载.

图7 加载导向装置Fig.7 Loading oriented apparatus

图8 试验测量装置Fig.8 Measuring apparatus
4.2 模型试验结果与分析
在模型试验土池的不同位置进行了不同加载方向的静承载力模型试验.模型试验结果表明:由于模型试验锚的长径比较大,土层和锚之间的摩擦系数很小,且模型锚的尺寸也较小,因此当加载方向从20°~40°变化时,锚的破坏均为竖向拔出的破坏模式,见图9(a),且锚破坏时在竖向平面内的转角不大于1°,故锚的运动基本为平动.静承载力试验还显示,在最后一级荷载作用下,锚的位移随时间逐渐增大,最终被拔出土层.显然,该级荷载大于或等于破坏荷载,又考虑到前一级荷载小于破坏荷载,为此取最后两级荷载的平均值作为锚的静极限承载力Ff.按这样的方法确定出的极限承载力在荷载位移曲线上对应的锚系泊点沿系泊方向的位移大约为0.6倍的锚径.据此,在循环承载力模型试验中,采用系泊点系泊方向的静位移与循环累积位移之和达到0.6倍锚径作为其破坏标准.
对于静荷载与循环荷载共同作用下的模型试验,选择加载方向为20°、30°和40°,每个加载方向又分别选择0.5和0.7的静荷载比进行试验.结果表明:相同加载方向的静荷载与循环荷载共同作用下,锚破坏时的竖向位移远大于其水平位移,且锚的转角很小,锚的破坏仍然是竖向拔出土层的平动破坏模式,见图9(b),这与静荷载作用下锚的破坏模式基本一致.在静荷载和循环荷载共同作用下,定义锚的承载力为破坏时静荷载与循环荷载的和,即

进一步,利用第3节中阐述的塑性上限分析方法,按每个循环承载力模型试验条件,计算预测相应的循环承载力,结果见表1.表中结果表明,预测结果与试验结果吻合较好.

图9 锚的破坏模式Fig.9 Failure mode of anchors

表1 计算结果与模型试验结果的比较Tab.1 Comparison between calculated and model test results
5 结 语
建议了一种基于塑性上限分析理论计算静荷载和循环荷载共同作用下软黏土中张紧式吸力锚循环承载力的方法.该方法首先假定在静荷载作用下吸力锚的破坏模式,并依据静力平衡原理计算静荷载在土体中产生的平均剪应力,然后依据循环剪切强度与土体平均剪应力和循环破坏次数的相互关系确定相应的循环强度,将循环荷载对土体的作用转化成土体强度的变化,再假定吸力锚在循环荷载下的破坏模式与静荷载作用下的破坏模式一致,并依照塑性上限分析原理和土体的循环强度计算强度变化后的承载力.为了验证该方法的合理性,进行了1g条件下的长径比为6,加载方向为20°、30°和40°,静荷载比分别为0.5和0.7的静荷载和循环荷载共同作用下吸力锚模型试验并应用该方法对模型试验结果进行了预测,预测结果与试验结果吻合较好.
由于模型试验锚的长径比较大、尺寸较小,锚侧壁的摩擦阻力与土的剪切强度之比较小,其破坏为竖向拔出土层的模式.进一步分析显示,当改变模型试验条件时,张紧式吸力锚的破坏也可能为水平破坏或竖直与水平均达到破坏的模式.因此,对于利用该方法对其他破坏模式下循环承载力的预测还需做进一步的试验验证.
致谢:本文工作得到王俊岭、李书兆与山传龙的帮助,在此表示衷心感谢.
[1] Rami Mahmoud El-Sherbiny. Performance of Suction Caisson Anchors in Normally Consolidated Clay[D]. Austin:University of Texas at Austin,2005.
[2] Dyvik R,Andersen K H. Field tests of anchors in clay I:Description [J]. ASCE,Journal of Geotechnical Engineering,1993,119(10):1515-1531.
[3] Andersen K H,Dyvik R. Field tests of anchors in clay II:Predictions and interpretation[J]. ASCE,Journal of Geotechnical Engineering,1993,119(10):1532-1549.
[4] Andersen K H,Jostad H P. Foundation design of skirted foundations and anchors in clay[C]// Offshore Technology Conference. Houston,USA,1999:383-392.
[5] Det Norske Veritas. Geotechnical Design and Installation of Suction Anchors in Clay[M]. Høvik:DNV Recommended Practice RP-E303,2005.
[6] 王建华,杨海明. 软土中桶型基础水平循环承载力的模型试验[J]. 岩土力学,2008,29(10):2606-2612. Wang Jianhua,Yang Haiming. Model tests on horizontal cyclic bearing capacity of bucket foundations in soft clays[J]. Rock and Soil Mechanics,2008,29(10):2606-2612(in Chinese).
[7] 李 驰,王建华,刘振纹. 软土地基单桶基础循环承载力研究[J]. 岩土工程学报,2005,27(9):1040-1044. Li Chi,Wang Jianhua,Liu Zhenwen. Cyclic bearing capacity of single bucket foundation on soft clay strata [J]. Chinese Journal of Geotechnical Engineering,2005,27(9):1040-1044(in Chinese).
[8] Andersen K H,Lauritzsen R. Bearing capacity for foundations with cyclic loading[J]. ASCE,Journal of Geotechnical Engineering,1988,114(5):540-555.
[9] Andersen K H. Bearing capacity under cyclic loadingoffshore,along the coast,and on land[J]. Canada Geotechnical Journal,2009,46(3):513-535.
[10] 李 驰,王建华. 饱和软黏土动力学特性循环扭剪试验研究[J]. 岩土力学,2008,29(2):460-464. Li Chi,Wang Jianhua. Cyclic torsional shear experimental studies on dynamic characters for saturated soft clay[J]. Rock and Soil Mechanics,2008,29(2):460-464(in Chinese).
[11] 王建华,曲延大. 循环应力作用下饱和软黏土的不固结不排水强度与破坏准则[J]. 水利学报,2011,42(6):672-677. Wang Jianhua,Qu Yanda. Unconsolidated and undrained strength and failure criterion of soft clay under cyclic stresses[J]. Journal of Hydraulic Engineering,2011,42(6):672-677(in Chinese).
[12] Aubeny C P,Han S W,Murff J D. Inclined load capacity of suction caissons [J]. International Journal of Numerical and Analytical Methods in Geomechanics,2003,27(14):1235-1254.
[13] Aubeny C P,Murff J D. Simplified limit solutions for the capacity of suction anchors under undrained conditions [J]. Ocean Engineering,2005,32(7):864-877.
[14] Murff J D,Hamilton J M. P-ultimate for undrained analysis of laterally loaded piles[J]. ASCE,Journal of Geotechnical Engineering,1993,119(1):91-107.
[15] 张学言,闫澍旺. 岩土塑性力学基础[M]. 天津:天津大学出版社,2004. Zhang Xueyan,Yan Shuwang. Fundamentals of Geotechnics Plasticity[M]. Tianjin:Tianjin University Press,2004(in Chinese).
Upper Bound Plasticity Method Determining Bearing Capacity of Suction Anchors with Cyclic Loading
Liu Jinglei1,2,Wang Jianhua1,2
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China;2. Geotechnique Engineering Institute of Tianjin University,Tianjin 300072,China)
Upper bound plasticity analysis is a method to calculate ultimate bearing capacity of suction anchors with static loads. It has not been reported how to calculate the bearing capacity of suction anchors under combined static and cyclic loads based on upper bound plasticity theory. An upper bound plasticity analysis method was presented to calculate the bearing capacity of suction anchors with taut mooring systems in soft clay under combined static and cyclic loads. Average shear stresses of soil elements due to the static load were first determined,which was based on the principle of static equilibrium for the method. Cyclic shear strengths of soil elements were further determined using the relationship between the cyclic shear strength and the average shear stress associated with the number of cycles to failure so that the effects of cyclic loads on soils transfered to changes of strength. It was further assumed that the failure mode of suction anchors under combined static and cyclic loads was the same as that under static loads. The bearing capacity of the anchors could be calculated using cyclic shear strength by the upper bound plasticity analysis. In order to verify the reasonableness of the method,model tests of suction anchors were conducted under the condition of 1g. The results of model tests were predicted using the method. Predicted results were basically in agreement with those of model tests.
suction anchors;cyclic bearing capacity;cyclic shear strength;upper bound plasticity analysis;model tests of suction anchors
TK421
A
0493-2137(2013)03-0224-08
2011-12-29;
2012-02-20.
国家自然科学基金资助项目(50879055).
刘晶磊(1981— ),男,博士研究生,kingbest_1118@163.com.
王建华,tdwjh@eyou.com.
