淤泥对平面钢闸门启门力影响的数值仿真分析

徐国宾，高仕赵，周富满(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

淤泥对平面钢闸门启门力影响的数值仿真分析

徐国宾，高仕赵，周富满
(天津大学水利工程仿真与安全国家重点实验室，天津 300072)

为了准确模拟闸前泥沙淤积对平面钢闸门启门力的影响，将闸前泥沙考虑为由粗细颗粒组成的宾汉体，闸门在开启过程中，粗颗粒之间的碰触和相对滑动产生了摩擦剪切应力，而细颗粒之间的絮凝作用在闸门开启的瞬间提供了极限剪切应力，这两种剪切应力之和称为泥沙临界屈服应力．闸门启动时，必先克服临界屈服应力．基于VOF(volume of fluid)的三维非稳态两相流TT-kε模型，引入宾汉体模型，考虑泥沙临界屈服应力，建立起闸前泥沙淤积对平面钢闸门启门力影响的数值仿真模型，并应用该仿真模型计算了天津宁车沽防潮闸在闸前有泥沙淤积情况下的启门力，计算结果与实测资料吻合较好．

平面钢闸门；启门力；数值仿真模型；临界屈服应力；宾汉体模型

修建在多沙河流上的一些水闸或水库，闸前及水库底孔前常出现不同程度的泥沙淤积现象．闸前泥沙淤积问题是一个在世界范围内普遍存在的问题，但是在中国北方的一些多沙河流这种现象特别严重，如：三门峡水利枢纽11号底孔平面钢闸门门前泥沙淤积厚度10.5,m，导致闸门开启困难；刘家峡水电站排沙洞门前泥沙淤积厚度为17.3～21.5,m；天津宁车沽防潮闸10号、18号钢闸门门前泥沙淤积厚度分别为1.6,m、3.6,m等．在闸前有泥沙淤积情况下，正确计算闸门启门力是摆在许多工程设计人员面前的难题.

根据文献[1]统计的实测资料，闸前泥沙由于长期处于淹没状态，在多数情况下属于宾汉体(Bingham)．宾汉体是一种具有一定屈服能力的非牛顿体．当其所受的外部载荷小于其临界屈服极限应力时，宾汉体表现为固体性质．当外部载荷超过了其临界屈服极限应力时，则其表现为黏性流体性质．泥沙中包含的粗颗粒和细颗粒分别提供了摩擦剪切应力和极限剪切应力，本文称这2种剪切应力之和为泥沙临界屈服应力．闸门启动时，必先克服临界屈服应力．

笔者基于VOF(volume of fluid)的三维非稳态两相流TT-kε模型，引入宾汉体模型，考虑泥沙临界屈服应力，建立起泥沙淤积对平面钢闸门启门力影响的数值仿真模型，并应用该模型计算了天津宁车沽防潮闸在闸前有泥沙淤积情况下的启门力变化过程，计算结果与实测资料吻合较好．

1 数学模型

1.1 流体控制方程

VOF方法由Hirt和Nichols[2]提出，适用于2种或2种以上互不穿透流体界面的跟踪计算．模型对每一项引入体积分数，通过求解每一控制单元内的体积分数来确定相间界面．对水和宾汉体之间的模拟，设φF为宾汉体的体积分数，对于每一个单元而言，存在3种情况：①φF=1，表示单元全部是宾汉体；②0＜φF＜1，表示单元一部分是水，一部分是宾汉体，存在水和宾汉体的交界面；③φF=0，表示单元全部是水．

连续方程为

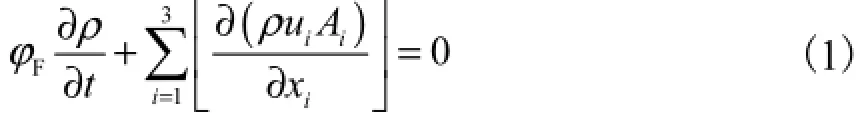
式中：Fφ为体积分数；iu为速度分量；ρ为流体密度；t为时间；iA为面积分数分量；ix为笛卡尔坐标分量．

动量方程为

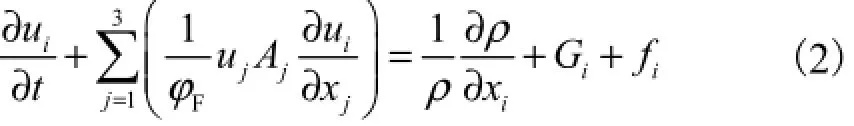
式中：iG为刚体加速度分量；if为黏性加速度．

流体体积函数为

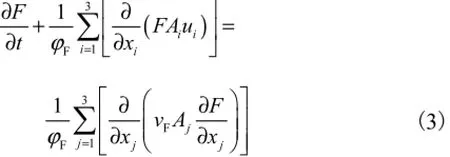
式中：Fv为扩散系数；F为流体体积函数．

紊动动能Tk方程为

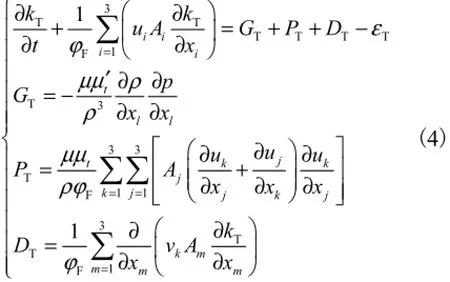
式中：kT为紊动动能；tμ和tμ′为紊动参数；TP和TG为紊流项；TD为扩散项；kv为扩散系数；Tε为稳定耗散率，其方程为

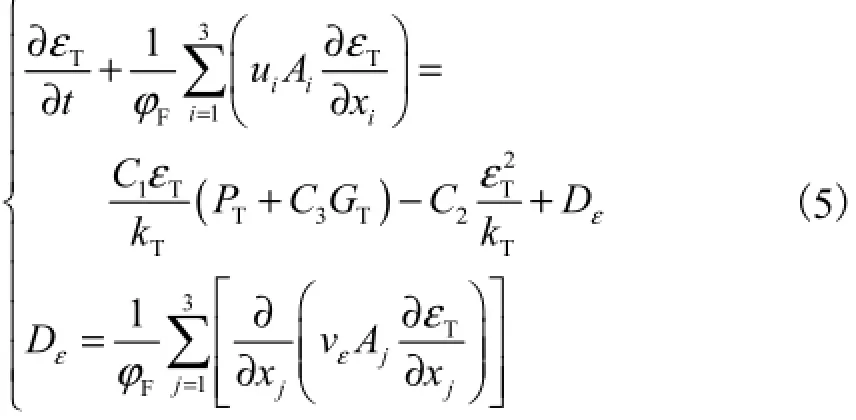
式中：1C、2C和3C为方程常数；Dε为扩散项；vε为耗散率系数[3]．

1.2 宾汉体计算模型

本文采用弹塑性模型计算宾汉体黏弹性变形阶段，而对其材料发生突变后的力学性质将采取松弛弹性应力的方法来实现．由图1可以得出弹塑性模型的总应力等于黏性应力和弹性应力之和．当受到外部载荷作用时将产生一定的弹性变形，在保持外载荷不变的情况下，弹性变形随着时间的推移而增加．如果进一步增大外载荷，当其材料的弹性应力超过临界屈服应力时，松弛弹性应力使其像黏性流体一样流动．宾汉体的总应力便可以认为是由带屈服极限的弹性元件和黏性元件产生的应力之和．

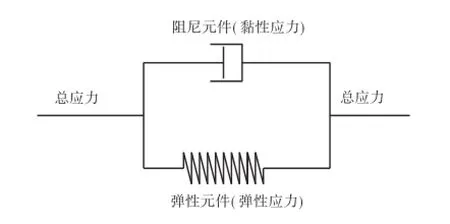
图1 弹塑性模型Fig.1 Viscoplastic model

宾汉体的总应力为

力；τi∗j为宾汉体的弹性应力．宾汉体的黏性应力[4]为

式中：ν为流体黏度系数；E˙ij为流体弹性应变率．

宾汉体的弹性应力[5-6]为

式中：τi′j为弹塑性模型的弹性应力；I2为τi′j的第2不变量；Γz为宾汉体临界屈服应力．

弹塑性模型的弹性应力为

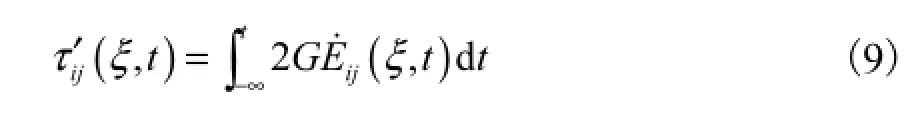
式中：τi′j(ξ,t)为弹塑性模型的弹性应力；G为弹性模量；E˙ij(ξ,t)为弹性应变率．

根据第4强度理论材料发生屈服是形状改变比能引起的，因此弹性元件松弛条件[5-6]为

1.3 泥沙临界屈服应力计算方法

泥沙中包含粗颗粒和细颗粒(当粒径d＜0.001,mm为细颗粒)[7-10]．在闸门开启过程中，粗颗粒之间的碰触和相对滑动产生了摩擦剪切应力；而细颗粒之间的絮凝作用在闸门开启的瞬间提供的是极限剪切应力，当闸门启动之后由于絮凝结构被破坏，细颗粒所提供的极限剪切应力迅速减小．这2种力组成了淤沙临界屈服应力，同时也是导致在闸前有泥沙淤积情况下最大启门力发生在闸门开启瞬间的主要原因．闸门开启的瞬间，泥沙临界屈服应力包括：① 粗颗粒之间的摩擦剪切应力；② 细颗粒的极限剪切应力．

宾汉体临界屈服应力表示为

式中：p′′为闸门所受泥沙的水平压力；f0为摩擦系数；τB为极限剪切应力；AD为泥沙与闸门接触面积总和．

式(11)中的摩擦系数估算式[11-12]为

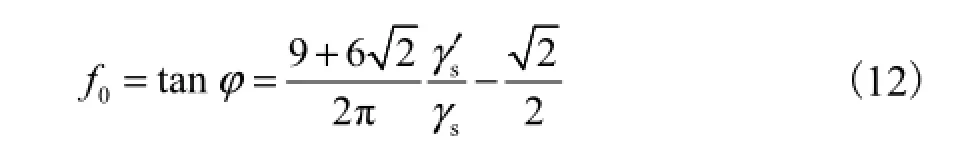
式中：φ为泥沙的休止角；γs′为泥沙干容重；γs为泥沙容重．

细颗粒之间的极限剪切应力[7]为

式中SV为体积计的泥沙浓度．单位宽度的泥沙压[13]为

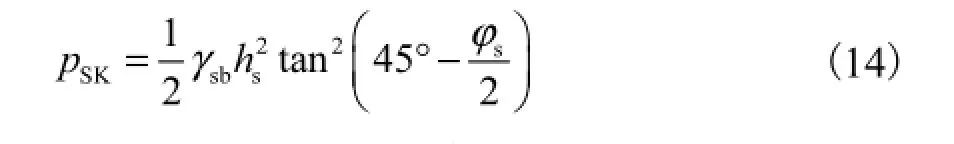
式中：pSK为泥沙压力标准值；γsb为泥沙的浮容重，γsb=γs′-(1-ε)γ，γ为水的容重，ε为泥沙的孔隙率；hs为闸门前泥沙厚度；φs为泥沙的内摩擦角．

根据文献[14]说明，φs=18°～20°(对于淤积时间较长的泥沙)；φs=12°～14°(较细的黏土质泥沙)；φs=0°(极细泥沙)．

闸门所受到泥沙的水平压力为

式中b为闸门宽度．

1.4 边界条件

求解上述方程的边界条件：计算区域出、入口采用压力(水位)边界条件，对于某一工况，上游水位是已知的，库区水流也比较平缓，采用静水压力分布．其他边界条件都采用对称边界条件．

2 模型应用

天津市宁车沽防潮闸位于潮白新河与永定新河交汇处．该防潮闸建于1971年，全闸为22孔开敞式，中20孔过流，两边孔以混凝土墙封堵．3号～18号孔的底板高程为-5.5,m，每孔净宽8.0,m，设置8.0,m×9.3,m开卧式平面定轮钢工作闸门(闸门自重为187.6,kN)．设计采用平卧式翻转闸门和下游正向轨(轨道由竖直段、圆弧（R=1.5m,θ=58°36′)和斜直段构成）．闸门下定轮中心距闸门底缘1.34,m，上定轮中心距下定轮中心3.98,m．正轨竖直段长7.5,m，圆弧段弧长1.533,m，斜直段的坡度为0.611,3[15]．

本文取天津宁车沽防潮闸实测数据和数值计算结果进行比对．泥沙的相关参数：容重为25,970.00,N/m3，φs取20°，干容重取12,500.00,N/m3，浮容重为7,783.00,N/m3．10号闸孔的相关参数为：上游水位高程-1.65,m，上游淤沙厚度1.80,m，下游水位高程0.40,m，下游淤沙厚度1.60,m．18号闸孔的相关参数为：上游水位高程-1.70,m，上游淤沙厚度3.05,m，下游水位高程0.86,m，下游淤沙厚度2.90,m．10号和18号闸门的相关参数为：闸门尺寸8.00,m×9.30,m；闸门厚度1.012,m，侧水封橡皮条的尺寸Φ,0.035,m×0.130,m×0.010,m×Φ,0.035,m，摩擦系数取0.20，两侧止水间距为8.00,m，滚轮半径为0.40,m，滚轴半径为0.080,m，滚动力臂为0.001,0,m，滑动摩擦系数为0.3，闸门下主梁距闸门底缘距离为1.34,m．根据式(11)计算10号闸门门前泥沙的临界屈服应力为2,666,Pa，18号闸门门前泥沙的临界屈服应力为4,203,Pa．

图2和图3分别为18号、10号闸门启门力数值计算结果及实测值．由图2可知18号闸门启门力的数值计算结果与实测数据趋势基本一致，由图3可知10号闸门的数值计算结果最大值为343,737,N，与实测数据最大值320,800,N的相对误差为6.7%，数值计算结果最大值与实测数据最大值基本相符．由图2和图3可得，用宾汉体来模拟门前泥沙所得结果与实际情况相符，同时也说明了本文提出的确定宾汉体临界屈服应力计算方法是合理的．

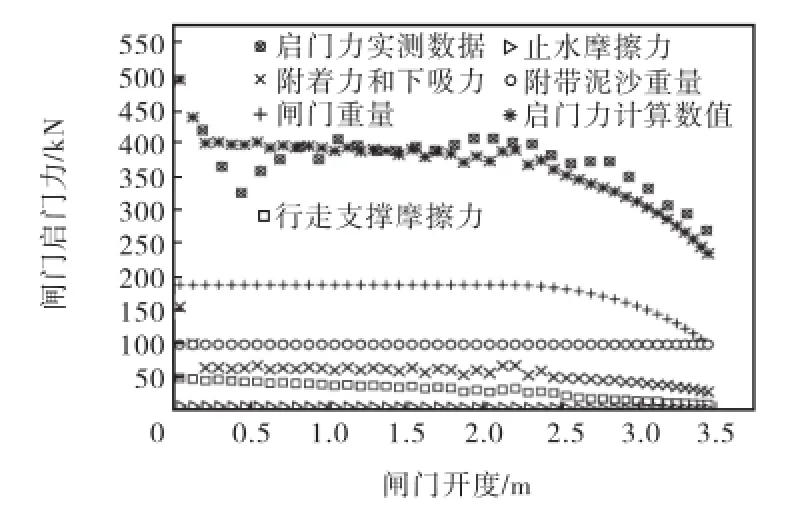
图2 18号闸门启门力数值计算结果及实测值Fig.2 Numerical results and the prototype observation data of the lifting force of No.18 gate

由图2～图4还可以得出闸门启门力Fq主要由下吸力px、附着力T、梁格附带泥沙重量G′、行走支撑摩擦力Tzd、止水摩擦力Tzs和闸门重量G几部分组成，此外闸门还受到水和泥沙的上下游压力pup、pdown．下吸力主要是由于闸下过流流态较差，水流在闸门底缘产生旋涡脱落导致的．闸门所受到泥沙的附着力主要由粗细颗粒提供的摩擦剪切应力和极限剪切应力组成．随着闸下过流流态由层流向紊流过渡，闸门所受的下吸力开始加强而附着力开始减弱，这样此消彼长导致了闸门所受到的合外力基本保持不变(如图2和图3所示)．对于水库中潜孔单向闸门，由图2和图3可知用宾汉体来模拟门前泥沙所得结果与实际情况相符，同时也说明了本文提出的确定宾汉体临界屈服应力计算方法是合理的．

长时间关闭情况下，其门顶将淤积一定厚度的泥沙；而对于像防潮闸这样的双向闸门，由于潮汐周期性涨落等原因导致了其梁格中也将淤积大量的泥沙．闸门必须克服这些泥沙的重量才能够开启，梁格中的泥沙重量主要集中在最下方主梁以上的梁格上，这也是引起闸门启门力增大的重要因素之一．因此在计算闸门启门力时应合理计算其值的大小．

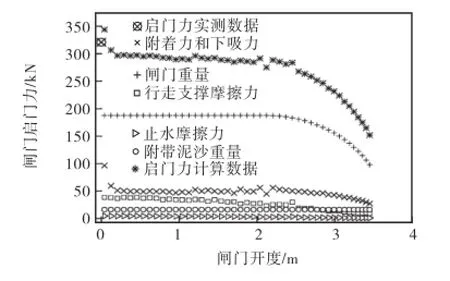
图3 10号闸门启门力数值计算结果及实测值Fig.3 Numerical results and the prototype observation data of the lifting force of No.10 gate

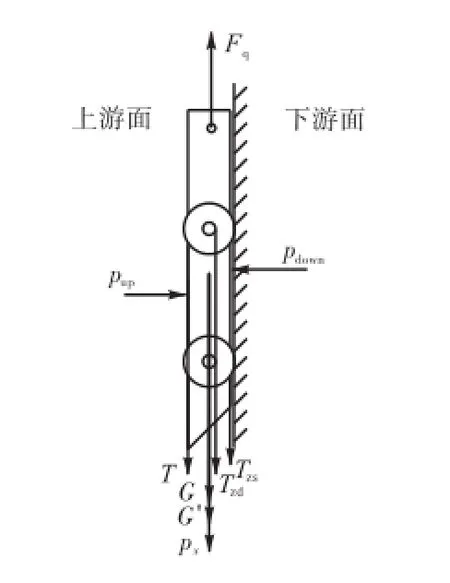
图4 闸门受力示意Fig.4 Sketch of the gate affected by forces

3 结 语

本文将泥沙考虑为由粗细颗粒组成，并分别提供了摩擦剪切应力和极限剪切应力，这2种剪切应力共同构成了泥沙临界屈服应力．闸门启动时，必先克服临界屈服应力．在闸前有泥沙淤积情况下，闸门启门力的最大值出现在闸门开启的瞬间．这主要是由于在闸门开启的瞬间，细颗粒之间的絮凝结构没有被破坏，其提供的极限剪切应力最大．随着闸门的开启，絮凝结构被破坏，其提供的极限剪切应力迅速降低，而后随着絮凝结构的重新组合，极限剪切应力有所增加．这是闸门启门力出现在开启瞬间的主要原因．本文给出的闸前泥沙淤积对平面钢闸门启门力影响的数值仿真模型，可以计算闸前有泥沙淤积情况下的启门力变化过程，计算结果与实测资料吻合较好．

参考文献：

［1］ 徐国宾，任晓枫. 坝前淤泥对闸门启门力影响的模拟相似性及方法[J]. 水利学报，2000(9)：61-64. Xu Guobin，Ren Xiaofeng. Study on similarity and modeling technique of model test for effect of sediment to lifting force of gate [J]. Journal of Hydraulic Engineering，2000(9)：61-64(in Chinese).

［2］ Hirt C W，Nichols B D. Volume of fluid(VOF)method for the dynamics of free boundaries[J]. Journal of Computational Physics，1981，39(1)：201-225.

［3］ 李人宪. 有限体积法基础[M]. 北京：国防工业出版社，2008. Li Renxian. The Basis of the Finite Volume Method [M]. Beijing：National Defense Industry Press，2008(in Chinese).

［4］ Malvern L E. Introduction to the Mechanics of a Continuous Medium [M]. USA：Prentice-Hall，Upper Saddle River，1969.

［5］ Hattel J H，Hansen P N. A control volume-based finite difference method for solving the equilibrium equation in terms of displacements [J]. Appl Math Modeling，1995，19(4)：210-243.

［6］ Brethour J M. Incremental Elastic Stress Model [M]. New Mexico：Flow Science Inc，2003.

［7］ 钱 宁. 高含沙水流运动[M]. 北京：清华大学出版社，1986. Qian Ning. Hyper-Concentrated Sediment Flow[M]. Beijing：Tsinghua University Press，1986(in Chinese).

［8］ Ajanta S，Dayakar P. Effect of microfabric on shear behavior of Kaolin clay[J]. Journal of Geotechnical and Engineering，2007，133(3)：306-318.

［9］ Salehi M，Sivakugan N. Effects of lime-clay modification on the consolidation behavior of the dredged mud [J]. Journal of Waterway，Port，Coastal and Ocean Engineering，2009，135(6)：251-258.

［10］ Yi Qitao，Kim Y，Tateda M. Sludge floc behavior in an elongated rectangular settling tank[J]. Journal of Environmental Engineering，2009，135(11)：1206-1212.

［11］ 石雨亮，陆 晶，詹义正，等. 淤沙的水下休止角与干容重计算[J]. 武汉大学学报：工学版，2007，40(3)：14-17. Shi Yuliang，Lu Jing，Zhan Yizheng，et al. Calculation of angle of repose and dry density of sediment [J]. Engineering Journal of Wuhan University，2007，40(3)：14-17(in Chinese).

［12］ 詹义正，谢葆玲. 散体淤沙的水下休止角[J]. 水电能源科学，1996，14(1)：56-59. Zhan Yizheng，Xie Baoling. Under water angle of rest for non-cohesive sediment[J]. International Journal Hydroelectric Energy，1996，14(1)：56-59(in Chinese).

［13］ 中华人民共和国电力工业部. DL 5077—1997 水工建筑物荷载设计规范[S]. 北京：中国电力出版社，1998. Ministry of Electric Power Industry of The People's Republic of China . DL 5077—1997 Specifications for Load Design of Hydraulic Structures [S]. Beijing：China Electric Power Press，1998(in Chinese).

［14］ 吴媚玲. 水工建筑物[M]. 北京：清华大学出版社，1991. Wu Meiling. Hydraulic Structures [M]. Beijing：Tsinghua University Press，1991(in Chinese).

［15］ 何成连，王大实，赵友鑫，等. 天津市宁车沽防潮闸闸门启闭力测试及分析[J]. 水利水电工程设计，2000，19(4)：36-38. He Chenglian，Wang Dashi，Zhao Youxin，et al. The testing and analysis of the opening and closing force about Tianjin Ningchegu Floodgate[J]. Design of Water Resources and Hydroelectric Engineering，2000，19(4)：36-38(in Chinese).

Numerical Simulation Analysis on Effect of Silt Sediment on Lifting Force of Plane Gate

Xu Guobin，Gao Shizhao，Zhou Fuman
(State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China)

In order to accurately simulate the effect of the sediment deposition on the lifting force of plane gates, the sediment in front of gates is considered to be Bingham which consists of the coarse and the fine particles. In the opening process, the contact and the relative slidingamong the coarse particles provide friction shear stress; Flocculation among fine particles provides the limit shear stress at the moment of the gate opening. The sum of the two kinds of stresses are known as the sediment critical yield stress. During thegate opening, the gate must overcome the critical yield stress firstly. Based on the three-dimensional, non-steady-state, two-phase-flow computed model kT-εTmodel and VOF(volume of fluid) method, the Bingham model was introduced in the paper. Considering the sediment critical yield stress, a numerical simulation model of the impact of sedimentation on gate opening was established. And the simulation model was applied to calculate the lifting force under the circumstances of sediment deposition in front of the gate of the Ningchegu floodgate in Tianjin. The results coincide with the prototype observation data well.

plane gate；lifting force；numerical simulation model；critical yield stress；Bingham model

TV222.2

A

0493-2137(2013)03-0197-05

2012-03-08；

2012-05-09.

国家自然科学基金资助项目(50979067)；国家自然科学基金创新研究群体科学基金资助项目(51021004).

徐国宾（1956— ），男，博士，教授，博士生导师，xuguob@sina.com.

高仕赵，wooden20030044@126.com.