基于自抗扰控制的2个耦合神经元间的混沌同步

张国山，李思瑶，王 江(天津大学电气工程与自动化学院，天津 300072)

基于自抗扰控制的2个耦合神经元间的混沌同步

张国山，李思瑶，王 江
(天津大学电气工程与自动化学院，天津 300072)

针对电缆神经元模型，利用自抗扰控制技术，研究并实现了通过间隙耦合的2个神经元间的混沌同步．未加入控制器时，混沌同步只有当神经元间的耦合强度较大时才会出现．然而在神经元系统中，此条件并不总是得以满足．为此采用自抗扰控制技术来实现混沌同步而不需要考虑耦合强度的大小．此方法不要求精确的神经元模型，而且不要求状态可测，对于外界扰动具有很强的鲁棒性．仿真结果证明所提方法是有效的．

非线性电缆神经元；间隙耦合；混沌同步；自抗扰控制

20世纪80年代，Matsumoto等[1]在做巨型乌贼轴突放电实验时，发现神经元(神经细胞)的放电模式呈现出周期、准周期、混沌等一系列复杂的非线性现象．从此，神经元的混沌行为引起了学者的广泛关注，其中常见的神经元模型有Hodgkin-Huxley(HH)、FitzHugh-Nagumo(FHN)、电缆模型等．文献[2]给出了电缆模型详细的建模过程及电缆神经元在外电场作用下的动态特性．由于很多神经元是通过间隙耦合[3]这种特殊的分子间通路来连接的，间隙耦合在细胞间的信息传输起着重要作用，因此在耦合神经元系统中成为研究热点．文献[4]研究了间隙耦合强度对系统稳定平衡点数量的影响，文献[5]研究了间隙耦合的电生理现象及建模过程，文献[6]在文献[2]的基础上，研究了通过间隙耦合连接的2个电缆神经元间的同步并讨论了耦合强度对于同步的影响．相关研究发现，耦合神经元间的混沌同步对于治疗癫痫、帕金森综合症等疾病具有重要意义[7-9]，神经元间同步的弱化会导致癫痫等疾病的发生．因此，研究实现神经元间的混沌同步，对于治疗神经类疾病有着重要的意义．

目前已有很多控制方法应用于耦合神经元间的混沌同步，文献[10]采用反馈线性化方法，文献[11-12]采用反步法，上述方法均要求状态变量是可观测的．文献[13]应用主动控制方法实现神经元间的混沌同步，应用此方法需满足控制对象参数精确已知的条件．文献[14-15]分别采用自适应鲁棒控制以及自适应H∞变论域模糊控制方法，分别实现了耦合HH神经元间的同步，由于其均为基于观测器的控制方法，因此不需要系统状态可测，具有适应性好、鲁棒性强等优点．

自抗扰控制技术由韩京清[16]提出，其特点是将所有未知参数视为总扰动，并利用扩张观测器估计此扰动，进而通过完全补偿而将其消除．因此它适用于参数未知、状态不可测的系统．此外，当输入信号突变时，自抗扰控制器能够平滑跟踪信号，从而减小输出误差，对于外界扰动具有很强的适应性与鲁棒性．在神经元系统中，由于神经元随时间变化不断衰老或发生变异，不易建立精确数学模型，且状态不易观测．因此，自抗扰控制技术的特点适用于实现耦合神经元间的混沌同步．笔者针对电缆神经元模型，利用自抗扰控制技术实现了通过间隙耦合的2个神经元间的混沌同步，仿真结果验证了所提方法的有效性.

1 间隙耦合神经元的动态特性

根据文献[2，6]，间隙耦合的电缆神经元模型表示为的周期振荡；当f增大为67时，进入混沌状态；之后，在经过一段很窄的混沌区域后，进入了锁相振荡状态；f继续增大到78时，处于2倍锁相振荡状态；当127.1131f＜＜时，神经元又处于混沌状态．本文选取129f=，即每个神经元均处于混沌状态时，来研究神经元间的同步，见图1～图6．

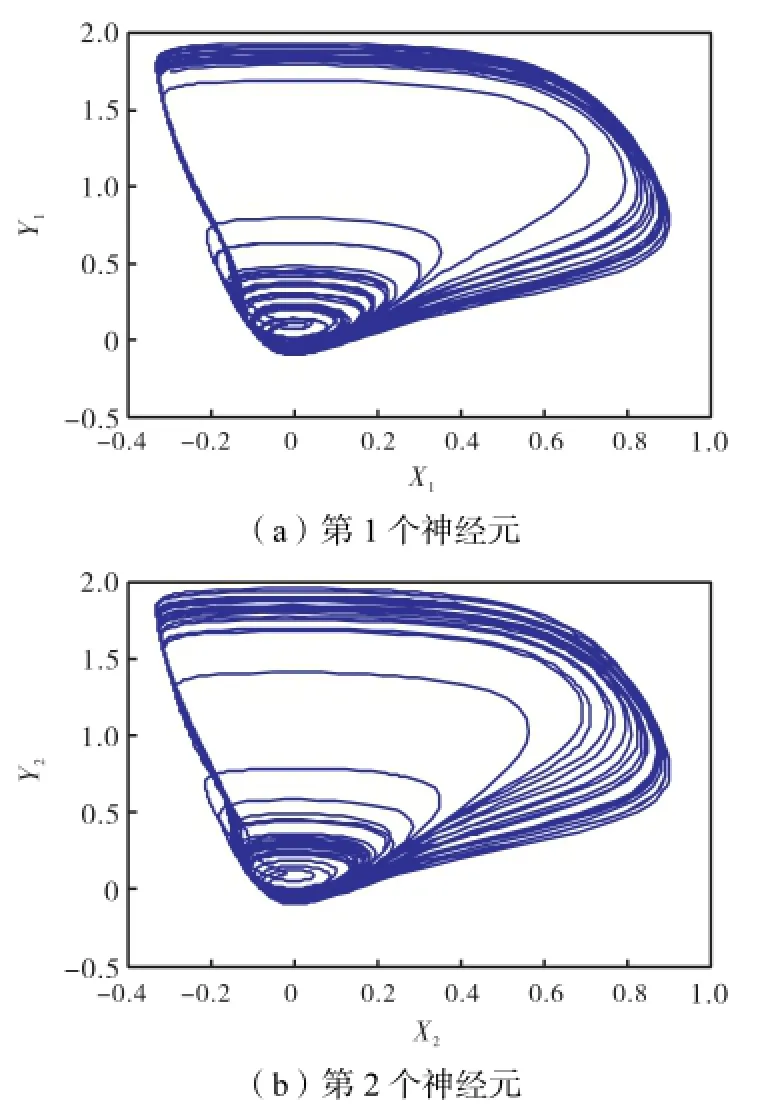
图1 2个神经元处于混沌状态(f=129，g=0.05)Fig.1 Two neurons in chaos(f=129，g=0.05)

图2 未出现神经元间同步的2个神经元状态的误差(f=129，g=0.05)Fig.2 State errors of two neurons without appearing the synchronization(f=129，g=0.05)

研究表明，当耦合强度相对较小(如g=0.05)时，同步不能发生，而当0.80g=(满足耦合强度要求)时同步才出现．图1～图3说明2个神经元没有同步发生，图4～图6说明实现了混沌同步．

图3 2个神经元状态的相平面表示(f=129，g=0.05)Fig.3 Phase planes of two neurons state(f=129，g=0.05)

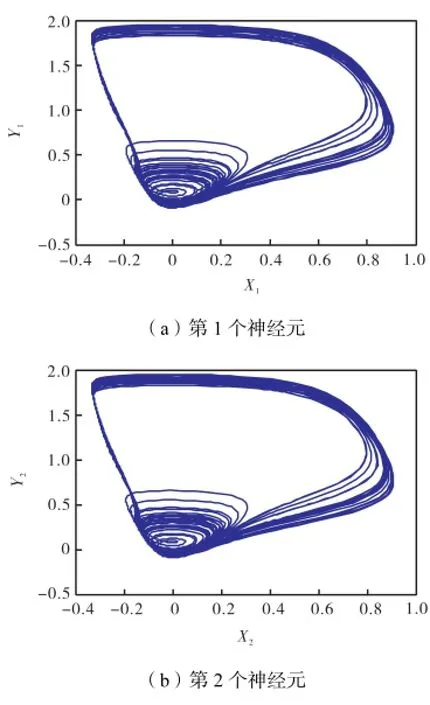
图4 2个神经元处于混沌状态(f=129，g=0.80)Fig.4 Two neurons in chaos(f=129，g=0.80)

图5 反映神经元实现同步的2个神经元状态的误差(f=129，g=0.80)Fig.5 State errors of two neurons reflecting synchronization (f=129，g=0.80)

图6 2个神经元状态的相平面表示(f=129，g=0.80)Fig.6 Phase planes of two neurons state(f=129，g=0.80)

当神经元系统发生病变或出现衰老时，神经元处于弱耦合的状态，因此需要一个控制器来实现混沌同步．

2 基于自抗扰控制2个耦合神经元同步

自抗扰控制器主要由4部分组成[16]：安排过渡过程，非线性组合，扩张状态观测器，扰动估计与补偿．

首先，安排过渡过程能够防止误差跳变，即：当输入信号突然变化为其他值，控制对象的输出仍能够平滑地跟踪输入信号．通常，安排过渡过程形式为

式中：1v为v的过渡过程；2v为1v的微分信号；0r与0h为控制参数；fhan为最速控制综合函数，即fhan=

式中sign为符号函数．

其次，在自抗扰控制器中，通常采用以下非线性函数的组合作为非线性组合，如最速控制综合函数fhan(x1,x2,r,h)，幂次函数

最后，给出自抗扰控制器中最重要的一部分：扩张状态观测器．由于本文研究的单神经元为二阶系统，首先考虑普通的二阶系统

式中()Ft可以未知．

实际上，可以将()Ft看作总扰动，为了消除未知扰动，将()Ft“扩张”为一个新的状态变量3x，同时

式中z1、z2、z3分别为x1、x2、x3的估计值，因此，扩张状态观测器能够给出未知扰动x3=F(t)的重要信息，从而构造出控制律u=(u0-F(t))/b，将系统(4)变为级联线性系统，形式为

式中u0=-fhan(x1,x2,r,h)．

在扩张状态观测器的作用下，就可以得到总扰动的估计并加以补偿．

综上所述，将安排过渡过程、非线性组合、扩张状态观测器以及扰动估计与补偿结合起来，得到自抗扰控制器的结构如图7所示．

图7 自抗扰控制器拓扑Fig.7 Topology of active disturbance rejection controller

自抗扰控制器的算法表示为

下面将自抗扰控制器应用于本文研究的耦合神经元间的混沌同步．加入控制器u后，系统(1)变为

正如前文所述，从控制理论的观点来看，同步问题可以看为一个跟踪问题．为了实现同步，令第1神经元为主系统，第2神经元为从系统，于是得到同步过程如下．

步骤1 通过安排过渡过程产生从系统所要追踪的信号(即主系统的输出)为

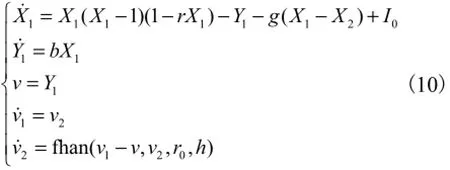
步骤2 利用扩张状态观测器估计从系统的状态，即

步骤3 构造控制信号

步骤4 给定控制信号，使从系统跟踪上主系统

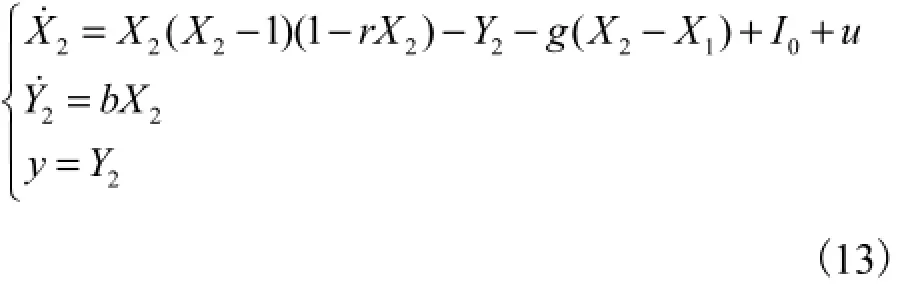
这里选取的耦合神经元参数与图1相同，即

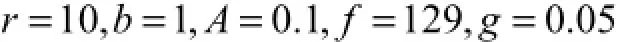
而控制器参数选定为

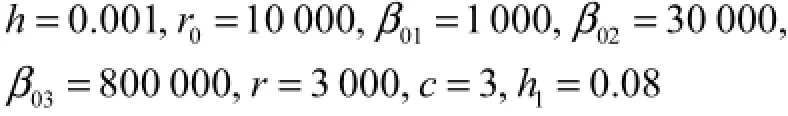
在t=200ms 时加入控制器，于是可以得到神经元间的同步，如图8所示．

图8 t=200 ms加入控制器后，实现了混沌同步Fig.8 Chaos synchronization achieved after the controller being added at t=200,ms

从图8可知，加入控制器之前，耦合神经元间的混沌同步并未出现．然而t=200ms 加入控制器后，第2神经元的输出误差迅速衰减为0(即实现同步)，证明了所加控制器的有效性．

由于自抗扰控制器可以估计出总扰动并最终消除扰动，因此它具有很强的鲁棒性与适应性．可以验证，如果控制器参数选为

仍可以实现同步，这说明自抗扰控制器的参数可以在大范围内进行调整而不影响控制性能．

3 结 语

当耦合神经元之间的耦合强度弱化时，基于自抗扰控制技术，设计了控制器，实现了耦合神经元间的混沌同步．本文结果为耦合神经元间的混沌同步提供了一种新方法．由于自抗扰控制器具有鲁棒性强、适应性好等优点，且各部分可独立设计，降低了实现难度．神经活动中的混沌同步，对于诊断及治疗神经类疾病来说具有重要意义．因此，本文结果对于神经疾病治疗、医疗器械开发等具有潜在的应用前景．

［1］ Matsumoto G，Aihara K，Hanyu Y，et al. Chaos and phase locking in normal squid axons[J]. Phys Lett A，1987，123(4)：162-166.

［2］ Thompson C J，Bardos D C，Yang Y S，et al. Nonlinear cable models for cells exposed to electric fields(I)：General theory and space-clamped solutions[J]. Chaos，Solitons & Fractals，1999，10(11)：1825-1842.

［3］ Bennett M V，Verselis V K. Biophysics of gap junction[J]. Seminars Cell Biol，1992，3(1)：29-47.

［4］ Baigent S，Stark J，Warner A. Convergent dynamics of two cells coupled by a nonlinear gap junction[J]. Nonlinear Anal，2001，47(1)：257-268.

［5］ Vogel R，Robert W. The electrophysiology of gap junctions and gap junction channels and their mathematical modeling[J]. Biol Cell，2002，94(7/8)：501-510.

［6］ Wang Jiang，Deng Bin，Tsang K M. Chaotic synchronization of neurons coupled with gap junction under external electrical stimulation[J]. Chaos，Solitons & Fractals，2004，22(2)：469-476.

［7］ Pyragas K，Popovych O V，Tass P A. Controlling synchrony in oscillatory networks with a separate stimulation registration setup[J]. Europhysics Letters，2007，80(4)：1-6.

［8］ Mormann F，Kreuz T，Andrzejak R G，et al. Epileptic seizures are preceded by a decrease in synchronization[J]. Epilepsy Research，2003，53(3)：173-185.

［9］ Simon J G L，Roger A B. Understanding the dopaminergic deficits in Parkinsons disease：Insights into disease heterogeneity[J]. Journal of Clinical Neuroscience，2009，16(5)：620-625.

［10］ Wang Jiang，Zhang Ting，Deng Bin. Synchronization of FitzHugh-Nagumo neurons in external electrical stimulation via nonlinear control[J]. Chaos，Solitons & Fractals，2007，31(1)：30-38.

［11］ Deng Bin，Wang Jiang，Fei Xiangyang. Synchronizing two coupled chaotic neurons in external electrical stimulation using backstepping control[J]. Chaos，Solitons & Fractals，2006，29(1)：182-189.

［12］ Wang Zuolei，Shi Xuerong. Chaotic bursting lag synchronization of Hindmarsh-Rose system via a single controller[J]. Applied Mathematics and Computation，2009，215(3)：1091-1097.

［13］ Sun Li，Wang Jiang，Deng Bin. Global synchronization of two Ghostburster neurons via active control[J]. Chaos，Solitons & Fractals，2009，40(3)：1213-1220.

［14］ Che Yanqiu，Wang Jiang，Zhou Sisi，et al. Synchronization control of Hodgkin-Huxley neurons exposed to ELF electric field[J]. Chaos，Solitons & Fractals，2009，40(4)：1588-1598.

［15］ Wang Jiang，Che Yanqiu，Zhou Sisi，et al. Unidirectional synchronization of Hodgkin-Huxley neurons exposed to ELF electric field[J]. Chaos，Solitons & Fractals，2009，39(3)：1335-1345.

［16］ Han Jingqing. From PID to active disturbance rejection control[J]. IEEE Trans on Industrial Electronics，2009，56(3)：900-906.

Chaos Synchronization of Two Coupled Neurons via Active Disturbance Rejection Control

Zhang Guoshan，Li Siyao，Wang Jiang
(School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China)

The chaos synchronization of two gap junction coupled neurons via active disturbance rejection control(ADRC)was investigated and achieved for the model of the nonlinear cable neuron. When the controller is not used，the synchronization will occur only if the coupling strength of gap junction is relatively big. But in the coupled neuron system，the condition can not always be satisfied. So in this paper，the chaos synchronization is achieved by adopting the active disturbance rejection control technique without considering the coupling strength of gap junction. This method does not require precise neural model nor measurable states，and it is robust to the external disturbance. Simulation results show that the proposed method is effective.

nonlinear cable neuron；gap junction；chaos synchronization；active disturbance rejection control(ADRC)

TP29

A

0493-2137(2013)03-0263-06

2011-09-29；

2012-04-25.

国家自然科学基金资助项目(61074088，61072012).

张国山（1961— ），男，教授，博士生导师.

张国山，zhanggs@tju.edu.cn.