提高滚动轴承套圈滚道和滚子精度的有序超精法

无锡机床股份有限公司（江苏 214061）胡建清

本文分析滚动轴承套圈、特别是大、中型轴承套圈或滚子超精加工后，轴承成品在使用中无法达到较高精度要求、回转精度不高，且可能在高速运转时产生较大噪声的原因，结合笔者长期以来的探讨和经验，分析选择一种科学获取超精参数的方法——有序超精法进行超精加工，以改善超精后的轴承套圈滚道，特别是大型轴承套圈滚道、滚子精度，从而满足高精度轴承的精度和低噪声要求。

这里所说的轴承套圈滚道是广义的，而滚子则主要是指调心轴承用的滚子（直径较大的腰鼓形柱体）。

1.产生超精参数选择不当原因

仅以圆柱滚子轴承的外圈进行滚道超精为例，结合轴承外圈滚道超精示意图（见图1），分析重要原因之一：模糊超精导致超精参数选择不当。

图1 轴承外圈滚道超精示意

图1中，A为轴承外圈滚道宽度，C为轴承外圈宽度，D为轴承外圈外径，d为轴承滚道内径，B为油石的宽度，W为油石的厚度（指油石与滚道超精面中点的切线方向上）。

模糊超精的实际超精参数极有可能因不当，从而导致轴承的滚道、滚子沿轴线剖面内的轮廓度在各圆周角度上不一致。例如在沿轴线与一个直径组成的剖面内滚道的直线度为0.003mm，但将轴承套圈旋转一个角度后检测沿轴线与另一个直径组成的剖面内滚道的直线度则变为0.002mm；并且轮廓形状也不同，前者可能为中凸偏左如图2a所示，最高点在距基准端面为a的位置，但后者可能变为中凸偏右如图2b所示，最高点在距基准端面为b的位置。以及滚道、滚子的圆度值在轴向各不同圆截面上不一致。例如在距滚道基准面轴向距离为a处测得的圆度为0.001 5mm，但在距滚道基准面轴向距离为b处的圆度可能就为0.002 5 mm了，并且圆度的形状也可能存在差异，从而该轴承圈在装配后的回转精度就不高，且在高速运转时会有较大噪声。而形成轴承的滚道、滚子沿轴线剖面内轮廓度在不同圆周角度上不一致，以及滚道、滚子的圆度值在轴向各不同圆截面上不一致且形状不同的原因，就是传统的习惯性对轴承套圈滚道、滚子的模糊超精形成的。

我们假设滚子磨削加工精度和轴承套圈终磨削加工精度都是理想的，以便于集中讨论轴承套圈终磨削后的超精过程；另外，可以从本文下面所叙述的有序超精原理，自然延伸和理解滚子的超精过程及其他种类套圈的超精过程，用相同的方法来解决所有类似的问题。

轴承业人士知道，在对如图1的轴承滚道进行超精时是由如下动作实现的：超精机工件主轴带动轴承套圈作旋转运动；油石通过气动或液动的压力将端头压在轴承套圈被超精的滚道面上，并在超精机的油石振荡架带动下，沿轴承套圈宽度方向作往复运动来达到对轴承套圈滚道表面进行超精加工的目的。

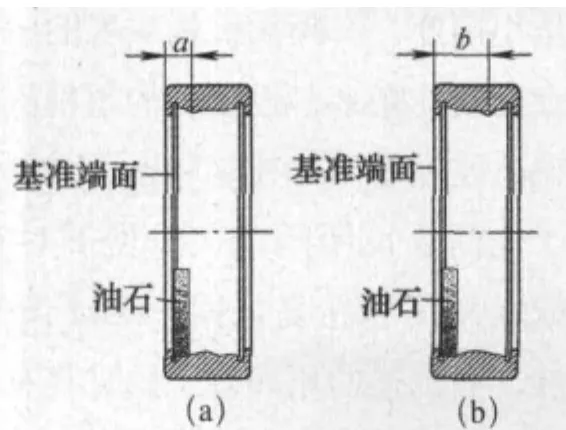
图 2

目前，国内外生产的超精机的主轴转动通常是采用直流或交流变频调速的，振荡架的振荡频率也是通过直流电动机或交流变频调速的，采用数控系统进行伺服控制工件主轴转速和振荡架往复运动的超精机极其罕见。即使是数控控制，一般会针对振荡头的往复运动速度和幅度进行控制，但超精机的工件主轴转速通常被认为没必要进行数控控制。国产超精机的使用说明书中通常都会在规格参数栏标明工件主轴的调速范围、油石振荡架的往复频率范围和往复幅度范围，有的超精机是将往复和振荡分开控制的，结构较复杂，即往复是大幅度小频次机构实现的，其移动幅度接近于滚道轴向全长；振荡是小幅度、高频次机构实现的，其移动幅度只有零点几或几毫米。但更多的超精机形式是：振荡动作就是往复动作，往复和振荡是同一个动作，本文为了能简要说明问题，以便于对有序超精的理解，就以振荡和往复是同一个动作作为研究对象。当然，所叙述的原理对于同时具有分开控制油石往复运动和振荡的超精机也是同样适用的。所以，本文以针对移动幅度接近于滚道轴向全长的往复加以叙述为主，简要附带分析移动幅度很小的高频振荡。

在轴承生产厂家的操作工对轴承套圈进行超精加工时，会将工件转速和油石振荡往复频率和幅度调到一个认为合适的区间，然后对被超精的轴承套圈进行超精加工，以规格大小不同来控制超精时间的长短。一般规格越大，所需超精的时间就越长，比如从几秒到几百秒不等。操作工对超精中转速、往复频率、时间这三个参数控制并不是精确的，实际是相当模糊的，通常依靠操作工的经验。在超精后用轮廓度仪检测，以检测结果进行参数调整，但这种调整又是模糊的，有时甚至调整后轮廓度变坏，比如有的操作工为了提高超精精度，便延长超精时间，结果却发现，延长超精时间所超出的轴承套圈的轮廓度反而比超精时间短的更差了。操作工就是在不断进行模糊调整并找到一个经检测，让自已感觉满意的参数后便固定下来，但在检测时，一般还不一定会进行同一零件的多个角度检测，所以导致误判的可能性很大。操作工超精轴承套圈中对径向剖面轮廓度在不同的圆周方向的状态模糊认识很常见，造成超精的滚道面不同圆周方向与基准端面（超精时轴承套圈与工件主轴接触的定位面）不对称、倾斜等，这种情况对中大型轴承套圈较易发生。因为超精的线速度相对是要恒定在一个合适范围内，线速度太慢会影响表面粗糙度和效率，但太快又会出现表面烧伤或粘铁，因此，线速度过慢和过快都影响超精质量。而且，所超套圈直径越大，套圈的超精转速就越小，越容易超坏滚道轮廓度。

那么，传统的超精方法问题出在哪里呢？

假如油石架的往复频率等于工件转速，比如工件主轴转速n=200r/m in，油石架的往复频率f=200次/m in，我们可以看到，当油石从轴承套圈的左侧移动到右侧，轴承套圈正好转了半转，而轴承套圈接下来的下一个半转结束，油石又正好从右移动到左侧；接下来轴承套圈再转一转时，油石又重复原来的轨迹超精了一个往复回到起点；当轴承套圈转了200转，油石沿原来的轨迹重复超精了200次，而轨迹外的轴承套圈表面就根本未被超精到，此时轴承套圈或超精的时间越长，滚道轴向轮廓度被破坏得越严重。这样的超精不但不能起到提高精度的作用，反而将原来终磨削时良好的精度给破坏了，装配后降低轴承旋转精度、增加噪声。

那么，如果把工件主轴转速n改为400r/m in，油石架的往复频率f 还是200次/m in不变，显然，当工件每2转油石便振荡一个往复，工件下一个2转，油石就重复原来的轨迹进行下一个往复。以此类推，我们可以发现，当工件转速等于油石振荡往复频率的倍数关系时，被超精的轴承套圈滚道的轮廓度会越超精越糟。

但是，是否工件转速除以油石往复频率只要不是倍数关系就可以超精好呢？分析发现并非如此，比如虽然未除尽，但余数很小，接近倍数关系导致油石的超精中心轨迹在下一个往复时与上一往复的轨迹偏离很小，接近重合，在有限的超精时间内超出的结果接近倍数关系的结果，同样不理想。一般工件转速除以油石往复频率越易除尽，油石沿原轨迹超精的可能性越大，超精效果越糟。那么，是否越不易除尽就越好呢？分析发现也非绝对如此，因为在有限的超精时间内，还是存在某些滚道表面未被超精到的可能性，而这种可能性，操作者又难以正确判断。因此，超精参数控制不当，实际是以往由于不知道如何控制转速与往复运动频率、或难以达到对参数的精确控制，才导致滚动轴承套圈超精加工后、在装配使用中无法达到高精度要求、且可能在高速运转时产生较大噪声的原因。而用以往的超精机是难以避开工件转速和油石往复频率的倍比情形、或近倍比情形的，在近倍比情形下操作者又不知道多长时间才能均匀完全超精。

2.寻求最佳超精参数

超精完成后，要正好使超精滚道表面能在每一沿轴线截面是均匀的，也就是在每一沿轴线截面的超精量在圆周各个角度是近乎相同的，避免在同一超精轨迹上重复超精，导致滚道另一些表面超精不到的情形发生，从而确保在各圆周角沿轴线截面的轮廓度是几乎相同的。

如图1所示，设轴承套圈在超精时的转速为n，也就是超精机的工件主轴转速；油石架的振荡往复频率为f，单件超精时间为t，通过几何与运动关系，计算各有序超精的参数。

（1）首先计算油石厚度W占用轴承套圈面的几何角α为

α=2arcsin（W/d）

（2）α占轴承套圈一周的比为

[ 2arcsin（W/d）]/360°=[arcsin（W/d）]/180

（3）如果油石一个振荡往复，而轴承套圈转动一转或若干转（m转）左右后（这里的m≥0，为方便计算，我们可以选1的扩大整数倍或缩小整数倍的值），油石刚刚不会与圆周起点与原超精轨迹完全重合，那么，轴承套圈的转数必须至少满足以下两点中的一点：

油石运动一个往复，轴承套圈的转数是

m+[arcsin（W/d）]/180°

表示转了m转后，正好多转过一个油石接触滚道的弧长角度的转数。

或者油石运动一个往复，轴承套圈的转数是

m－[arcsin（W/d）]/180°

表示转了m转后，正好少转过一个油石接触滚道的弧长角度的转数。因此油石一个往复，轴承套圈的转数应当是

m±[arcsin（W/d）]/180°

两者可选其一。

（4）当在轴承套圈表面完整进行均匀超精，至少需要对油石进行多少个往复呢？分析得出至少需要往复次数为

360°/2arcsin（W/d）=180°/arcsin（W/d）

（5）完成超精一个轴承套圈，工件主轴至少需要转动多少转，转数为

{m±[arcsin（W/d）]/180°}×180°/arcsin（W/d）

=180°m/arcsin（W/d）±1

我们发现：理论上要完成一个均匀超精过程，如果不去考虑超精光整要求的话，最少工件要转±1转即一整周，+表示正转；－表示反转。当然，在实际使用中只需用正转即可，为超精出光整的工件，m也极少会取0，因为如果工件真的只转1转，虽然能均匀超精整个轴承套圈，但很显然是远远无法达到光整要求的，因此，m会取远大于1的数。

完成一个轴承套圈的均匀超精过程，工件主轴转数至少应当满足：180°m/a rcsin（W/d）±1的整数Z（这个整数用字母Z表示，是完成一个均匀超精的周期，当Z=1时，仅仅对超精面均匀超精了一个周期，还远远不能完全达到表面光整要求的作用）倍，显然，油石架往复次数必须是180°m/arcsin（W/d）的相同整数Z倍。当Z等于1时是正好能超精完整一个周期，也是均匀超精至少要的周期；当Z等于2时，就超精了两个周期；当Z选择几就是超精几个周期；如果要超精得彻底些，就将Z选大些，但效率会降低，反之效率就高些，这就要在实际超精实践中，按不同大小规格的零件进行适当选择，兼顾考虑。

（6）以上第5条是满足要求的极限条件，并且让油石宽度B＝0的情形下。但在实际超精过程中，由于油石宽度绝对不可能是0，而是有一个宽度B的，所以在油石进行第二个往复时会与上个往复在宽度面积部分重合，重合部位的超精量在重合超精中较小，与超精时轨迹完全重合的情况绝然不同，不但不会破坏轮廓度，相反还起到光整表面的作用。如果我们想让重合的面积增大些，就只需调整W的计算值用W′替代，为此，让超精油石在每一个往复过程中与前次往复人为在圆周方向有更多重合，实现这一目的的措施是：将计算公式中的油石厚度W乘以小于1的数，比如选0.9，这样W′=0.9W，公式中的W计算时用W′代替，这样计算的结果相当于是以0.9倍W厚度而宽度B＝0的油石的极限超精状态，而实际为W的厚度和B≠0的效果会优于极限状态。当然用W′这样算参数会延长超精时间，降低效率，但能超精得更均匀彻底。不过，通过上述分析可以清楚地看到，因为油石存在B≠0的宽度值，所以，一般情况下无需用W′去替代W，而是直接用W值算就已经足够了。

3.实例计算

设超精一个滚子轴承套圈内径滚道，如果被超精滚道d=300mm；滚道宽度A=50mm；选了厚度W=20mm；宽度B=5mm的油石。确定一下有序超精时全部超精表面至少要超精多少转数（如果选m=1转）？油石至少要往复多少次？

解：至少要超精转数=180°m/arcsin（W/d）±1=180°/arcsin（20/300）±1=47.09±1转

小数应进位，所以47.09±1转，得出49转和47转，这里要注意：有余数时，见余数就进到个位：即47.09转直接进位为48转；若选公式中的+1转就进位后加1转；若选公式中的－1转就进位后减1转。

那么，为什么要进行进位而不是退位呢？这是因为当选m=1、按油石厚度W=20mm、滚道内径是300mm时，算出的转数为47.09转，当我们选取47转时，会发现转动一圈时留下一小部分未超精到，而留下的部分又无法在下一个循环中均匀被超精，超精弧长与余量的关系不再是均匀的。而进到48转时，每个循环的油石W两端会有一小部分是重叠超精的，此时相当于将实际厚度是W的油石当成厚度为W′的油石来超精的，显然，W′＜W，且保证了48转均匀分摊了进位的0.91转，并可以在下一个48转循环时保持均匀超精。

油石至少要往复的次数=180°m/arcsin（W/d）=180°/arcsin（20/300）= 47.09次，得出48次，即：有余数时直接进位即可，道理同上段所述，与转数同步。这里选m=1转，计算的结果有助于我们对有序超精的理解，可以看到，当超精完一个周期，油石往复的次数是48次，而工件转数至少为要么49转，要么47转，转数与油石往复次数只需差正好1，这正是有序超精的绝妙之处，就是这个差数1，让油石不再对滚道上仅仅对超精过的部分进行重复超精，而是进行了一个均匀分布的超精，有效达到确保不破坏滚道轮廓度的作用。

当然，可以在设定时选择49转倍数Z=2倍、3倍甚至更多整数倍。而往复次数也要相应选Z=2～3倍甚至更多倍变动，否则将破坏形状。还要注意，油石的往复幅度加上油石的宽度要尽可能大，不能小于滚道宽度。

在操作时还可以选Z=1，而m选扩大整数倍值或缩小整数倍的值，可以不增加往复次数，同样确保了全部均匀超精到。当选择的超精线速度相同时，如果轴承套圈较小，则应选择扩大的m整数值；如果直径较大，则应选择较小的m整数倍值。但是当直径很大，可能超精线速度又不能太大时，可以选择m为缩小整数倍的值，比如m=0.5转，m=0.25转等。

通过上述计算我们还可算出单件轴承套圈的超精时间，比如，当我们需要超精的线速度为1.5m/s时，当选Z=4倍转数时，单件超精时间按+1转的算是：49πd×4/1.5=123.15s；或按－1转的算是：47πd×4/1.5=118.12s。

如果要设定往复频率，按+1转的算是：48Z/123.15=48×4/123.15=1.559 1s－1。

按－1转的算是：48Z/118.12=48×4/118.12=1.625 5s－1。

实际超精中，如果m值较小，则一个周期是远远不够的，因为一个周期很可能还远远不能对轴承套圈的滚道或滚子的波峰去除，即远远不能完全达到光整要求，而仅仅是达到均匀超精的要求，因此，应当在实际超精中选较大的周期值Z值，才能达到光整的要求。

显然，我们为了得以精确控制，必须使用工件主轴和往复轴双轴联动伺服控制的超精机进行加工。

这里顺便提一下，如果是油石小振荡和往复运动分开控制则需三轴联动。小振荡的振荡次数应选择往复的整数倍，比如选5倍的话，那么例题中就是48×4×5=960次。如果要精确设置振荡频率，或用+1转算：960/123.15=7.795 3s－1；或用－1转算：960/115.61=8.303 8s－1

由于大多数生产超精机机床的企业对上述超精原理并未重视，或认识不足，或者就根本未考虑到，因此，目前同时用数控系统联动控制工件主轴、油石往复运动频率二轴联动的还未发现有，而再加小振荡频率数控控制的机械三轴联动的超精机床更是没见到。这其中的原因可能是因为对中小规格的轴承套圈由于可选择较大的工件转速，使m值较大，使工件转速与往复频率比值较大， 由于m值较大，因此轮廓度破坏不很明显。但是，对于大型套圈，因为线速度不能过度提高，因此，m值就不能选得大，导致工件转速与往复频率成倍数比例关系的可能性变大，对轮廓度影响就很大；如果按上述有序超精的分析计算方法，实现全数控的、清晰参数化有序超精法超精，可以避免同一位置过度超精、局部位置漏超精现象，会大大提高大型轴承套圈（或大型滚子）的超精精度等级，又因为避免了无把握的盲目超精，因此也可提高超精效率，让超精精度和效率处于严格可控之中。

归纳化简以上论述过程，总结一下完成超精一个轴承套圈或滚子，工件主轴需要带动轴承套圈或滚子转动多少转呢？我们就用N表示转数

公式中的Z≥1，整数；m≥0（可取1的整数倍）。

当在轴承套圈表面完整进行均匀超精，需要油石往复多少次呢？我们就用P表示往复次数

如果将小振荡与往复是分开控制的机床，那么，小振荡次数应当是多少次呢？我们就用p表示小振荡次数

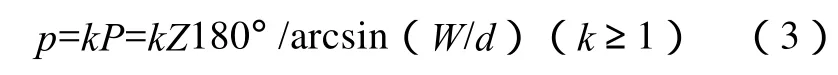
单件超精时间是多少呢？我们就用t表示单件超精时间，v表示超精切线速度

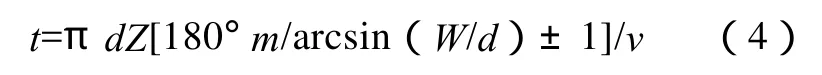
往复频率是多少呢？我们就用f 表示往复频率

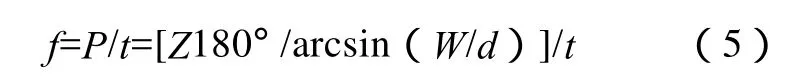
如果小振荡与往复是分开控制的，那么，小振荡频率是多少呢？我们就用f ′表示小振荡频率

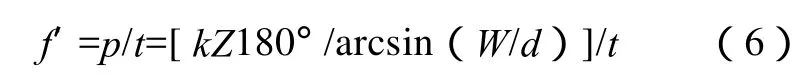
以上公式内容和使用注意事项，已经在前面论述中说过，此处就省略了。

4.关于三轴联动超精机设计的个人总体观点

工件主轴、油石架大往复移动和油石架小幅度振荡三轴联动会大大提高超精机复杂程度，笔者个人观点是：不用小振荡结构的超精机因结构相对简单，所以超精效果较为稳定可靠，有工件主轴转数与往复运动次数两轴联动，对于通常轴承套圈滚道的超精已经足够满足要求，大型滚子也一样。当然，如果设计师能找到并设计出较为合理结构的、包含小振荡的三轴联动超精机，那么，笔者当然也并不反对。

对于超精机，有一个动作需要注意，就是主轴在带动工件开始转动计数的前提，必须是在油石已可靠压在工件的被超精表面上时，并且油石架与主轴同时起动和计数、或油石压上工件的一瞬间这一点开始，对工件转数和往复运动次数同时进行计数，这很重要，否则可能会影响完全均匀进行超精，让有序超精的效果打折。实现这一精确计数的传感器应当精心调整，计数完成的一瞬间同样油石应迅速抬起，确保有序超精发挥好的效果。

5.结语

通过认识有序超精原理，可以正确指导超精参数选择，操作者也做到心中有数，避免在超精过程中走弯路。通过前面的理论计算，得出合适的超精参数，来避免由于模糊超精所带来的对大型轴承套圈或大型滚子超精后、沿轴线剖面内的轮廓度在各圆周角度上不一致、且在沿轴向各不同位置的圆截面圆度值不一致的现象，对于有效提高超精精度及超精效率起到无与伦比的作用，是确保超精后的轴承套圈和滚子在装配后、改善旋转精度和降低噪声的、行之有效的一条捷径。

此外，虽然轴承套圈超精机与滚子超精机的结构是不同的，但有序超精原理是相通的，建立在一样的上述数学模型基础上，为此，文中作了合并讲述。