球轴承沟道超精研运动干涉分析

高作斌,郭星成,杨晓波

(河南科技大学 机电工程学院，河南 洛阳 471003)

沟道是球轴承运转时最主要的内部工作面，其表面质量对轴承运转时的摩擦、磨损、温升、噪声等均有重要影响[1]。超精研是球轴承沟道的终加工工艺，对沟道表面质量有决定性影响[2]。与高端装备和重大装备配套的高性能轴承对套圈沟道表面质量及其均匀性和一致性要求很高。在轴承生产中，直径等尺寸参数普遍采用严格的在线自动检测；相比之下，沟道表面质量，尤其是表面质量均匀性的严格检测十分困难，因而保证表面质量更加依赖稳定、高水平的加工工艺。针对高性能轴承的加工需求，深入开展球轴承套圈沟道超精研工艺的相关研究，形成更高水平也更加稳定的加工工艺技术，具有十分突出的重要性。

超精研是一种以油石为工具的研磨加工工艺，主要用于改善精密零件表面的波纹度和粗糙度。研磨工艺中，工具与工件表面的接触问题对加工质量和加工效率都有十分重要的影响[3]。在平面、圆柱面和球面等常见表面的超精研加工中，油石工作面与工件表面的形状完全吻合，两者处于稳定的面接触状态，而且整个工件表面的不同位置具有相等的机会与油石接触，这为有效去除整个工件表面的微观波纹和粗糙峰提供了良好条件[4]。然而，目前的球轴承沟道超精研工艺中，理论上油石工作面与套圈沟道表面存在运动干涉，使得两者的接触不是一种面接触[5-6]；基于油石的易磨损特性，运动干涉的存在使得油石与沟道的接触研磨过程成为一个动态变化的复杂过程。因此，深入研究油石与沟道之间的运动干涉规律，对于理解和解决球轴承沟道超精研质量问题具有重要意义。

一些文献[7-8]提出了新的超精研方法以求避免或减弱运动干涉的不良影响，也有研究[9-10]利用接触分析商业软件对油石磨损和套圈材料去除过程进行了仿真分析。然而，上述研究远不够全面和深入。由于深沟球轴承、角接触球轴承、推力球轴承等不同类型轴承套圈沟道的超精研方式有很大程度的类似性，为了进一步探索球轴承沟道超精研工艺中油石与套圈运动干涉的特征，以深沟球轴承内圈沟道超精研方式为代表建立运动干涉数学模型，针对油石工作面与套圈沟道表面的运动干涉问题进行理论分析和数值模拟。

1 运动干涉的数学模型及分析方法

1.1 深沟球轴承内圈沟道超精研方式

深沟球轴承内圈沟道超精研方式如图1所示，套圈围绕自身轴线做定轴转动，油石以一定压力浮动地压在套圈沟道表面并做定轴摆动，其摆动轴线垂直于套圈轴线并经过沟道的沟形圆弧中心。长方形油石摆动的中心位置(初始位置)和姿态为：宽度中心平面经过其摆动轴线，厚度中心平面经过套圈轴线，一个端面正对着套圈沟道并压在上面。

图1 深沟球轴承内圈沟道超精研加工方式

与套圈沟道接触的油石端面称为油石工作面，在油石投入使用前，油石工作面的初始形状需要修整为与沟道形状吻合。一条油石一般可以加工许多个中小型套圈，在其整个使用过程中，油石的工作面并不需要像砂轮那样用修整器进行修整，其形状由油石自身磨损决定。

1.2 数学模型及分析方法

超精研之前，套圈沟道是经过磨削加工的圆环面。假定油石工作面的初始形状已经修整为与沟道形状完全吻合的圆环面，油石处于初始位置(摆动中心位置)。

建立如图2所示的与套圈沟道及油石关联的正交三维坐标系Oxyz，y轴与套圈轴线重合，x轴与油石摆动轴心线平行，xOz平面是摆动轴心线所在平面。BC为油石厚度中心平面截得的沟形圆弧，AD为x轴正向油石厚度边界平面在沟道圆环面上截得的曲线，AB和CD分别为沟道两侧边缘圆弧，曲面ABCD为套圈沟道圆环面的一部分；O1为yOz平面上的沟形圆弧中心，O1x1为油石的摆动轴心线，O1y1为与y轴平行的辅助轴线。

图2 与套圈沟道及油石关联的正交三维坐标系

油石和套圈的基本几何参数为：油石摆动轴心线至套圈转动轴心线间的距离R；套圈沟形圆弧半径r；沿y轴度量的套圈沟道宽度B；沿x轴度量的油石厚度T；合适的油石宽度需略大于套圈沟道宽度，并保证油石摆动到一侧的极限位置时，另一侧的油石边缘刚好进入沟道。

基于油石的摆动方向，油石与套圈的干涉只发生在套圈沟道宽度与油石厚度所限定的区域内，将此区域称为干涉区，其x和y坐标的范围为

在干涉区内，沟道圆环面方程为

(1)

初始位置的油石工作面与套圈沟道圆环面重合，因此，(1)式也是干涉区内初始位置的油石工作面方程。

如图2所示，在沟道宽度范围内取任意一平行于xOz的平面，截曲面ABCD得圆弧EF，交O1y1轴线于点O2(0,y,R)；在油石厚度范围内取任意一平行于yOz的平面，截曲面ABCD得曲线JK，交圆弧EF于点M(x,y,z)，交油石摆动轴心线O1x1于点O3(x,y,R)。当油石摆动β角度后，初始位置油石工作面上的点M摆动至点M1(x,y1,z1)，相应地，圆弧EF摆动至E′F′。由于曲面ABCD是绕套圈轴线回转而形成的圆环面，并不是以油石摆动轴线为轴线的回转曲面，所以点M1和圆弧E′F′都不在曲面ABCD上。这意味着摆动β角度后的油石工作面将不再与套圈沟道表面重合，这就是油石与套圈发生运动干涉的几何学基础。

求摆动β角度时油石工作面方程的方法为：首先建立点M1与点M坐标之间的关系，然后将这种关系代入(1)式，得到表示点M1的3个坐标之间关系的表达式；由于摆动后油石工作面的形状并无变化，点M1又是与点M对应的任意点，这个表达式实际上就是摆动β角度时的油石工作面方程，只是其坐标符号与Oxyz坐标系不一致，因此，将这个表达式中的坐标符号进行相应修改，即可得到在坐标系Oxyz中表达的摆动后的油石工作面方程。

点M1和点M均在图2中O3MM1平面上，其x轴方向坐标相同，因此只需考察这2个点在y轴和z轴方向的坐标关系。O3MM1平面上点M，M1和O3之间的位置关系如图3所示，点M和点M1到O3的距离均为rm(rm为点M的摆动半径)。

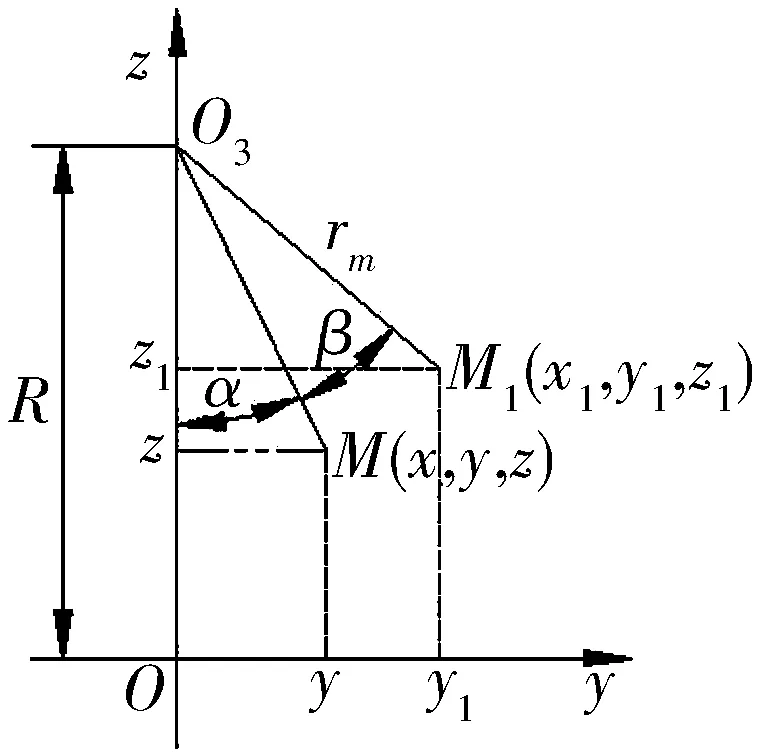
图3 yOz坐标平面上投影后的各点位置关系示意图

设MO3与z轴的夹角为α，根据图3，点M1和点M的坐标可表示为

y1=rmsin(α+β)，

(2)

z1=R-rmcos(α+β)，

(3)

y=rmsinα，

(4)

z=R-rmcosα。

(5)

将(2)式和(3)式展开得

y1=rmsinαcosβ+rmcosαsinβ，

(6)

z1=R-rmcosαcosβ+rmsinαsinβ。

(7)

将(6)式两边同乘cosβ，(7)式两边同乘sinβ然后相加并整理得

rmsinα=y1cosβ+zsinβ-Rsinβ，

(8)

将(8)式代入(4)式可得

y=y1cosβ+z1sinβ-Rsinβ。

(9)

将(6)式两边同乘sinβ，(7)式两边同乘cosβ然后相加并整理得

rmcosα=y1sinβ-z1cosβ+Rcosβ，

(10)

将(10)式代入(5)式可得

z=z1cosβ-y1sinβ+R(1-cosβ)。

(11)

摆动前后点M与点M1的x坐标不变，因此有

x=x1。

(12)

将(9)，(11)，(12)式代入(1)式整理后可得摆动β角度的油石工作面的方程为

z1cosβ-y1sinβ+R(1-cosβ)=

(13)

为便于比较摆动β角度的油石工作面与套圈沟道表面之间的位置差异，将2个曲面方程的变量符号进行统一，即将(13)式中的y1修改为y，x1修改为x，同时，为与沟道表面的z向坐标在符号上能够区分，z1符号保持不变，用以代表摆动β角度的油石工作面上任意一点的z向坐标，从而得到干涉区内摆动β角度的油石工作面方程为

z1cosβ-ysinβ+R(1-cosβ)=

(14)

在干涉区范围内，对于任意一组x和y的值，根据(1)式可以算得对应的z值，从而得到沟道表面任意一点的坐标值；根据(14)式可以算得对应的z1值，从而得到摆动β角度的油石工作面上任意点的坐标值。

如果从z坐标方向考察油石与套圈的干涉情况，则可以定义一个称为z向干涉量的参数dz为

dz=z-z1,

(15)

显然，dz值为正，两者干涉；dz值为负，两者不干涉；dz值为零，两者刚好接触。

2 运动干涉分析

2.1 干涉量分布

根据(1)，(14)式计算所得干涉区内沟道表面与摆动后油石工作面的位置对比如图4所示，图4的计算条件为：R=17 mm，r=4 mm，T=8 mm，B=6 mm，β=18°。当油石向y轴正向摆动时，β取正值;反之,β取负值。

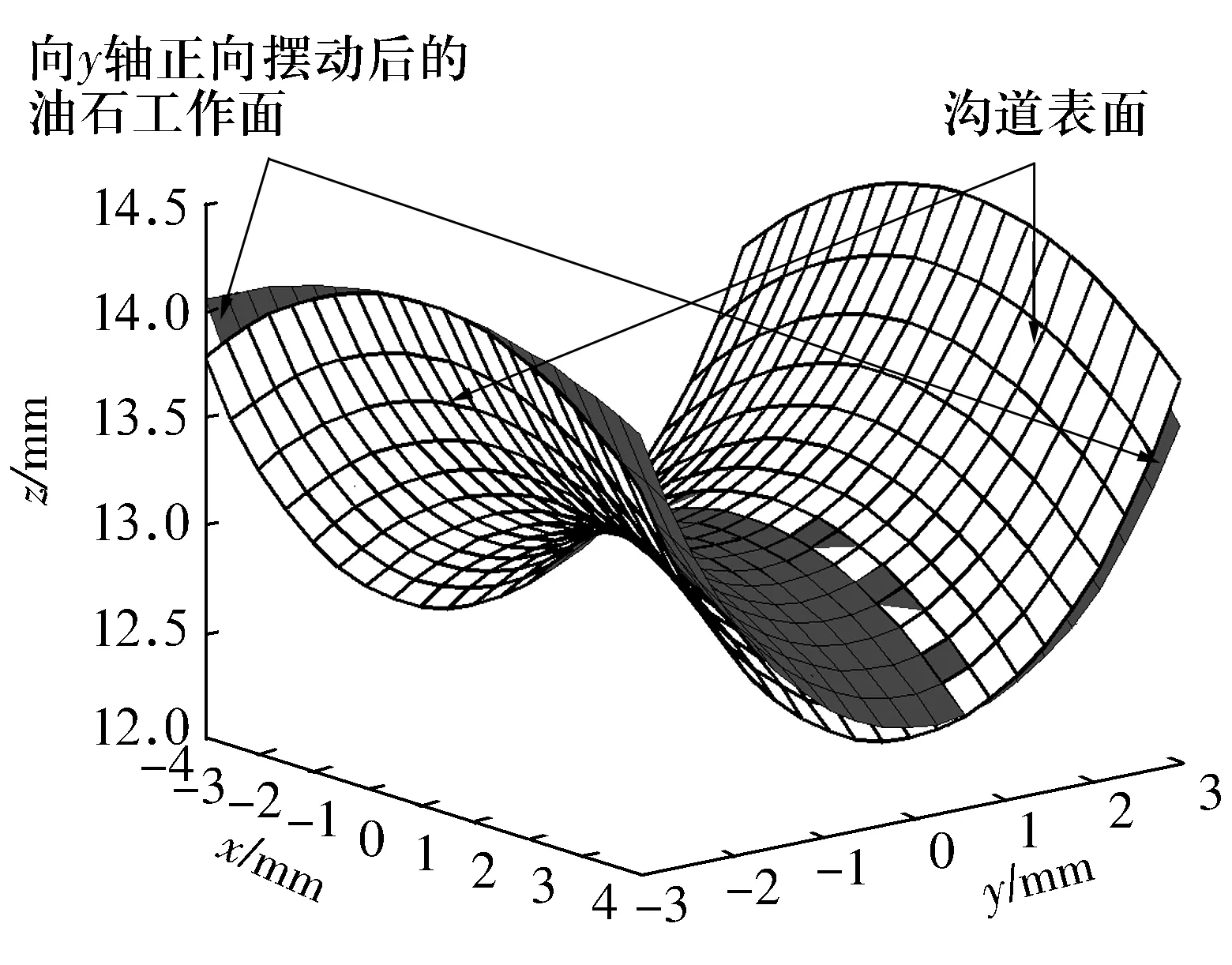
图4 摆动后油石工作面与沟道表面的位置对比

从图4可以看出：在z坐标方向，向y轴正向摆动后的油石工作面，一部分处于沟道表面下方，会发生干涉；而另一部分处于上方，不会发生干涉。由于油石向y轴正向摆动，干涉发生在y>0的一侧，这正好是摆动时油石所偏向的一侧。沟道表面和初始位置的油石工作面都关于y=0平面对称，油石摆动轴也在y=0平面上，根据对称性，当油石向y轴负方向摆动时，必然在y<0的一侧有干涉，这仍然是油石所偏向的一侧。

根据(1)，(14)，(15)式计算所得干涉区内摆动后油石工作面与沟道表面的z向干涉量分布如图5所示。由图5a可知，随着在xOy平面上位置的不同，z向干涉量大小是变化的，有正值，有负值，还有一些位置干涉量为零。总体上，干涉量的绝对值随着x和y绝对值的增大而增大。

图5b给出了干涉量为零的平面作为参考平面，以便更直观地判断存在干涉的区域及相应的干涉量分布。处于参考平面上方表示干涉，处于参考平面下方表示不干涉，而处于参考平面上表示油石与沟道表面刚好接触。图5b表明干涉只发生在y>0的区域。

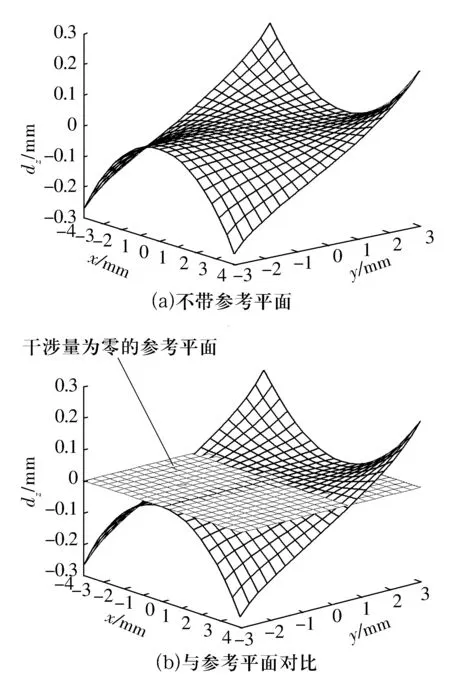
图5 摆动后油石工作面与沟道表面z向干涉量分布

基于上述干涉量分布特征，考虑到油石的双向摆动，可以推断：在干涉区四角位置，即油石厚度方向2个侧面与沟道宽度2条边缘线的4个交点处，干涉量是最大的，图4计算条件下z向最大干涉量为0.210 7 mm。对图4计算条件进行多种修改，包括改变摆动角度β的大小和正负值，计算干涉量及其分布，结果表明，虽然干涉量的具体数值不同，但均表现出上述分布特征。

2.2 主要几何及运动参数对干涉程度的影响

图4计算条件中所列的几何及运动参数都会对干涉量的大小和分布产生影响。套圈的几何参数在被加工的套圈型号确定后不能改变，不予分析。油石几何参数中，油石宽度选择空间很小，不必分析，所以只分析油石厚度。运动参数中，只有油石摆动幅度对干涉程度有影响。油石摆动幅度就是油石摆动过程中摆动角度β由小到大变化所达到的最大值，因此，其影响可以根据计算条件中油石摆动角度β的影响进行分析。

2.2.1 油石厚度

保持图4其他计算条件不变，仅改变油石厚度T，计算相应的z向干涉量最大值dzmax，得到dzmax随T变化的曲线，如图6所示。

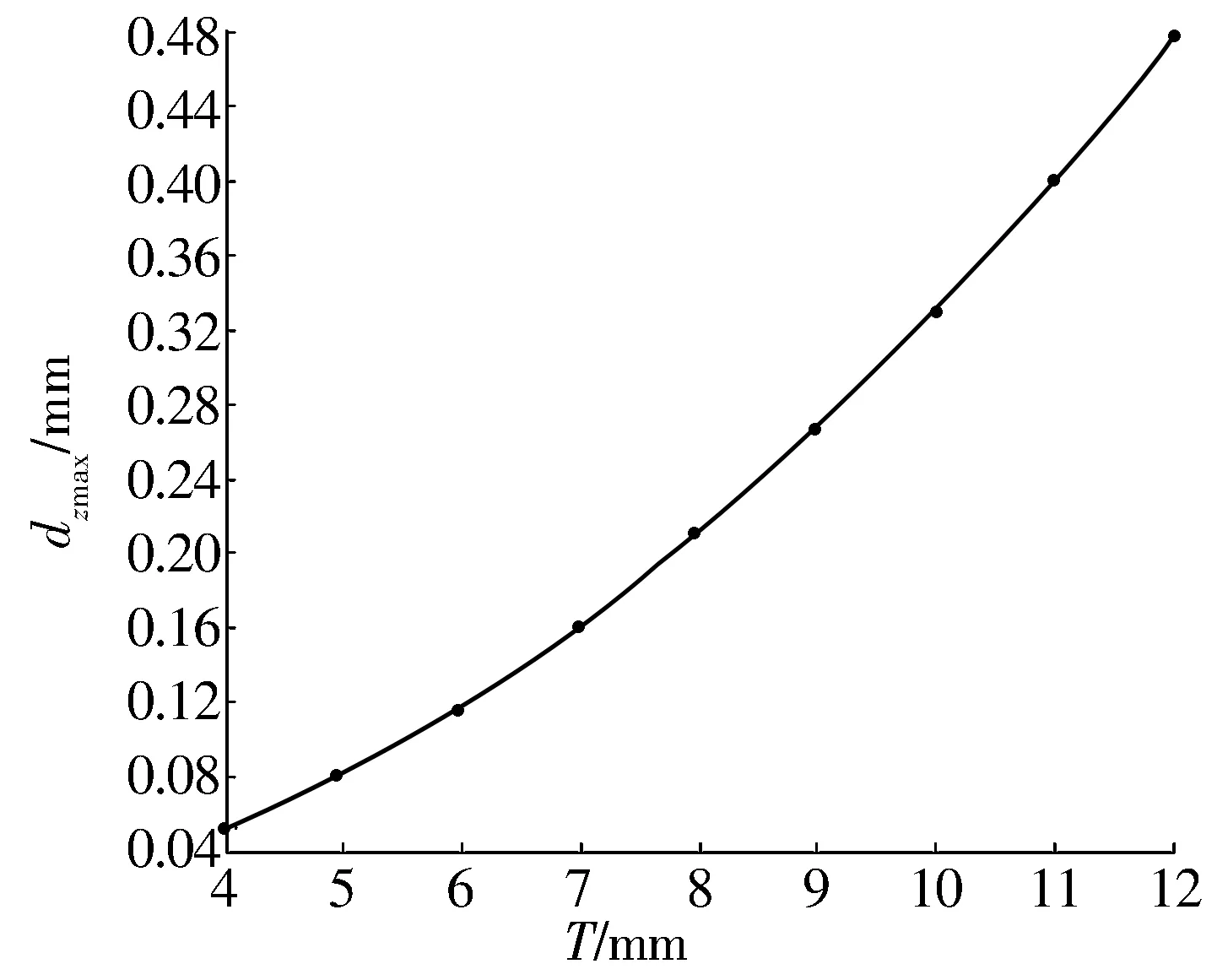
图6 油石厚度对z向干涉量最大值的影响

图6中的曲线向右上方倾斜并向上翘，这表明，所选用的油石厚度越大，干涉越严重，而且油石厚度单位增加量引起的干涉量增加值也越大。在图6的计算条件下，油石厚度从5 mm增大到10 mm时，z向干涉量最大值dzmax从0.080 5 mm增大到0.330 0 mm，这表明油石厚度对干涉程度的影响很大。

2.2.2 油石的摆动角度与摆动幅度

保持图4其他计算条件不变，仅改变油石摆动角度β，计算相应的z向干涉量最大值dzmax，得到dzmax随β变化的曲线，如图7所示。

图7 油石摆动角度对z向干涉量最大值的影响

从图7可以看出，油石摆动角度增大时，最大干涉量随之增大，呈近似线性的单调增长趋势。图7计算条件下，油石摆动角度从6°增大到24°时，z向干涉量最大值dzmax从0.079 7 mm增大到0.257 9 mm；油石摆动角度每增大1°，dzmax增大约0.009 9 mm。

油石摆动幅度是球轴承沟道超精研加工的重要工艺参数，在超精研之前进行选择。上述关于油石摆动角度对干涉影响的分析表明，在油石往复摆动的过程中，其经历的每一个位置，油石工作面与沟道表面的干涉程度都不同，所在位置对应的摆动角度越大，干涉程度就越大。这意味着在选择油石摆动幅度时，其取值越大，所产生的干涉就越严重。

3 结论

球轴承沟道超精研过程中，油石与套圈之间的运动干涉的特征和影响因素如下:

1)干涉量分布是不均匀的，干涉程度随着油石摆动角度的变化而不断变化。

2)沟道表面上，在任一瞬时，干涉只发生于油石摆动所偏向的一侧；沟道边缘与油石厚度侧面交界处干涉量最大，越靠近沟道宽度中心或油石厚度中心位置，干涉量越小。

3)影响干涉程度的因素既有几何参数,也有运动参数。油石厚度越大，干涉越严重；干涉程度随着油石摆动角度的增大而增大，油石摆动幅度选取越大，运动干涉越严重。