11—14岁学生关于可能性比较的认知发展研究

何声清，巩子坤

（杭州师范大学 理学院，浙江 杭州 310036）

1 问题提出

概率作为研究随机现象规律性的科学，它从偶然因素和影响中寻求必然的、本质的规律，并对这些偶然性影响给以数量的刻画和分析．了解某个随机现象的随机性是指既知道这个随机现象中所有可能出现的结果，又知道每个结果出现的可能性大小（概率），也就是要知道相应的随机变量分布．对于义务教育阶段的学生而言，数学课程标准提出用实验、模拟、构造样本空间等方法计算简单等可能事件的可能性大小（概率）[1]．因而，基于精确的样本空间判断可能性和可能性大小，也就成为学生掌握概率知识的一个重要目标．

Piaget和Inhelder对儿童概率概念进行过最早、最全面的研究，并描述出了儿童概率认知发展的3个重要阶段[2]．第一阶段，即前运算阶段，发生在7岁或8岁之前，该阶段的儿童还没有机遇或者概率的概念．第二阶段为具体运算阶段，年龄从7、8岁到12岁左右，能区分确定性和不确定性，开始知道如何量化概率，但在计算复杂情境的概率时拥有的是一套不完整的对策．直到12岁前后，即形式思维阶段开始时，儿童能将演绎逻辑与随机概率统合起来，进行比较精确的概率计算．在之后的研究中，有研究者认为Piaget低估了儿童的认知能力，而有的研究者认为即便是西方发达国家，儿童的概率认知也没有达到Piaget的发展阶段[3]．对中国而言，《全日制义务教育数学课程标准（2011年版）》已经降低了概率部分的要求和难度，第二学段要求认知随机性，第三学段才要求对可能性的大小数量化，这在一定程度上耦合了Piaget关于概率认知划分的阶段．概率概念是在形式思维阶段发展起来的，这里正是参考Piaget和Inhelder的研究成果，针对处于形式思维阶段的11—14岁学生，考察其对于可能性比较的认知发展情况，探讨影响学生可能性比较认知的因素，分析学生在可能性比较过程中的典型错误认知及其成因，对课程标准及课堂教学中关于概率内容的目标定位提出若干建议．

2 方 法

2.1 被 试

被试分为11—14岁4个年龄组，每个年龄115人左右，共457人．各年龄组被试分别来自不同类型的学校：杭州市区重点中小学两所（学校类型标记为 1），城乡结合地区普通中小学两所（学校类型标记为2）和农村中小学两所（学校类型标记为 3）．每个类型学校的年龄组被试在 38人左右．按照性别不同，被试分别被标记为1（男生）和2（女生）．根据被试父母职业，划分1—6个类型；根据被试父母学历，划分1—5个水平．

2.2 设计与材料

每个被试要求完成一份相同的测试问卷，问卷配有插图．问卷共5个题目，题目情境均是从一个不透明的盒子中摸出一个或两个球，盒中的球大小一样、手感相同、颜色不同．并且根据“球的颜色”、“盒中球的个数”、“摸出球的个数”3个变量，使5道题呈现良好的衔接和梯度．具体问题见表1．

2.3 程序及计分

实验以笔试形式在班级统一进行，限定答题时间，由本校老师监考，并向被试强调本次测试是正规考试，要求被试认真作答．另外，考虑到影响学生可能性比较水平的某些可能相关因素，测试材料除了要求被试认真填写学校、年级、出生年月、性别等信息之外，还在测试最后设置家庭信息栏，要求被试填写父母职业和父母学历信息．

研究只考虑被试对每一题的第3小题的作答情况，根据学生的语言解释，将学生对于可能性大小的比较按低到高分为4个水平：主观判断，记0分；基于部分样本空间，记1分；基于模糊的样本空间，记2分；基于精确的样本空间，记3分．

3名研究人员依据计分标准对被试的答案单独打分，一致性达到97%．

2.4 关于可能性大小比较的4个水平划分标准及其解释

关于被试对于可能性大小比较的水平划分，研究人员根据被试每题第3问的语言解释做出断定．主观判断：被试的解释反映个人喜好、唯心主义、经验主义等；基于部分样本空间：被试能够基于样本空间解决可能性大小的比较问题，但不能构建精确的样本空间；基于模糊的样本空间：这是一类基于特殊部分样本空间的情形，由于其具有很强的普遍性和研究意义，故单独作为一个水平，并且认为这种水平高于一般的基于部分样本空间水平．这个水平主要是针对第 4和第5题而言的，包括被试构建的两种样本空间情形，即“黑球、黑球，白球、白球，黑球、白球”和“黑球、黑球，白球、白球，黑球、白球，白球、黑球”这两种情形；基于精确的样本空间，被试能够明确指出各种可能性的概率（精确量化），对可能性大小进行判断．

3 结 果

3.1 关于测试题目的结构效度

问卷共有4套题目，各套题之间的得分相关都达到了显著水平（0.130~0.656之间），说明5道题的内部一致性很高，问卷具有良好的结构效度（见表2）．

表2 各测试题之间的相关性

3.2 11—14岁学生可能性比较认知水平的发展趋势及特征

3.2.1 11—14岁学生可能性比较的总体认知水平

总体来看，11—12岁学生的可能性比较总体认知水平呈现上升趋势，13岁开始出现停滞甚至下降趋势（见图1）．

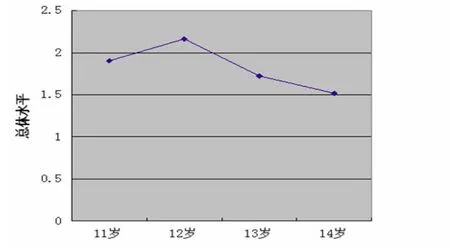
图1 11—14岁学生可能性比较的总体认知水平

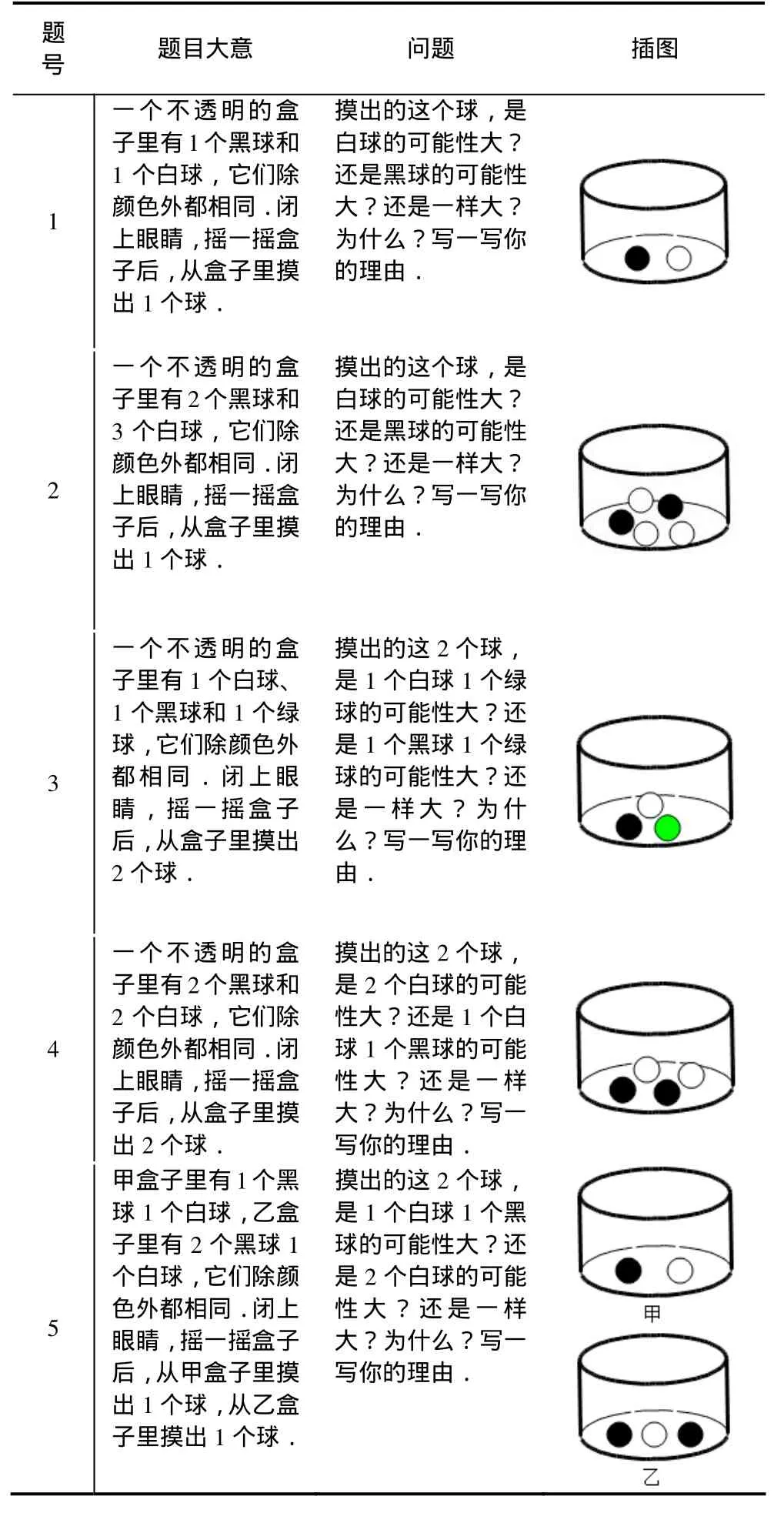
表1 11—14岁学生可能性比较调查问卷

以学生的年龄为自变量，以学生的可能性比较的总体认知水平为因变量，进行单因素方差分析，初步结果表明，Levene(3, 210)=5.548，P<0.001．也就是说，不同自变量分组的方差不齐，没有通过方差齐性检验．“无法满足方差齐性假设并非方差分析最致命的问题，特别是多个样本组大小相等时．如果多个样本组的大小不等，则推荐使用 Welch方差分析．”[4]进而选择使用 Welch方差分析，Welch(3,104.373)=13.514，P<0.001．表明，在可能性比较方面，不同年龄学生间存在显著性差异．

由于没有通过方差齐性检验，于是选择了 Dunnett T3方法进行多重比较检验，结果如表 3所示．结果表明，11—12岁之间，11—13岁之间，13—14岁之间差异不显著（P>0.05）．其余年龄之间的差异非常显著（P<0.05）．

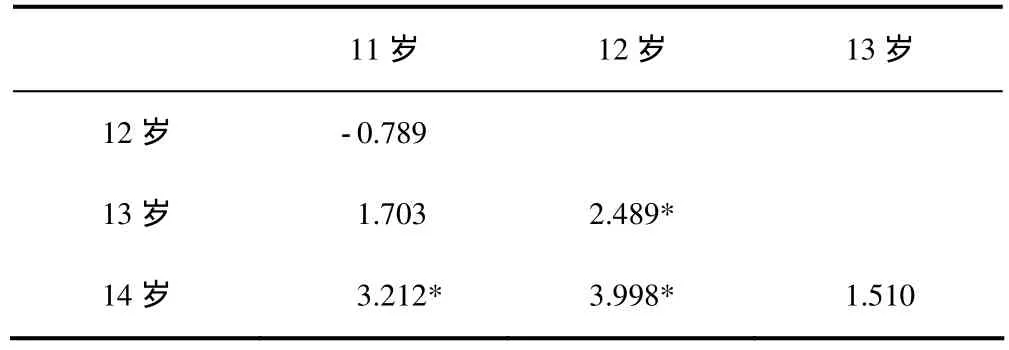
表3 11—14岁学生可能性认知总体水平的多重比较

由此进一步得出，学生在11—12阶段关于可能性认知，处于缓慢发展阶段；12—13岁，处于倒退发展阶段；13—14岁，处于停滞发展阶段．

3.2.2 不同情境下11—14岁学生可能性比较的认知水平发展趋势及其特征

考察不同情境下11—14岁学生可能性比较的认知水平发展趋势及其特征，为此统计了每一题不同年龄的平均水平．结果表明，对于第1、2题，各年龄段的平均水平基本持平并且水平均值接近“3”．由此看出，对于各年龄段学生来说，“摸出一个球”（即单一样本）情境下的可能性比较，学生能够构建良好的样本空间，对可能性大小做出判断，且在11岁时就基本达到基于精确的样本空间水平．

考察第3、4、5题，即“摸出两个球”情境下的可能性比较，学生的平均水平明显偏低，这也是导致其总体水平偏低的原因．

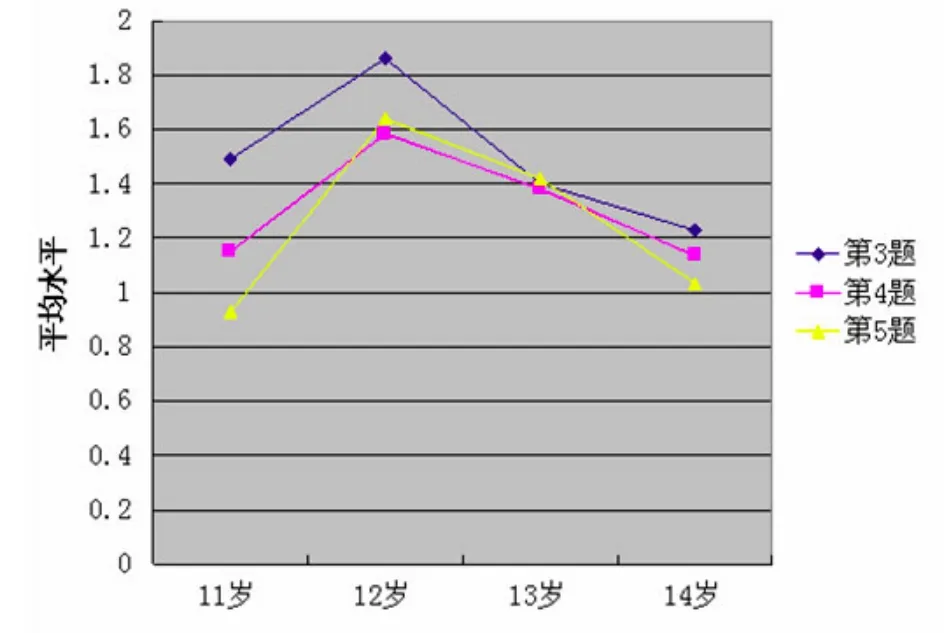
图2 11—14岁学生“摸出两个球”情境下的可能性比较的平均水平

综上得出，11—14岁学生在“摸出一个球”情境下的可能性比较的水平均达到“掌握”的水平；在“摸出两个球”情境下的可能性比较总体水平偏低，说明学生的组合认知可能是其对可能性大小进行比较的一个影响因素；并且在“摸出两个球”情境中11—14岁学生经历了从发展到停滞发展甚至倒退发展的过程，这也反映了其总体水平的发展趋势；学生在第3题的平均水平高于第4、5题，说明重复样本对学生构造样本空间造成困扰．

3.2.3 重复样本条件下“摸出两个球”情境时可能性比较的认知水平

进一步考察重复样本条件下“摸出两个球”情境时可能性比较的水平，为此统计了第4、5两题学生可能性比较的4种水平的百分比（见表4）．数据显示：对于在重复样本条件下“摸出两个球”情境时的可能性比较，有相当一部分甚至过半学生只能凭借主观判断可能性的大小，另外有相当一部分学生处于构造模糊的样本空间判断可能性大小的水平；相对于从同一总体抽取组合样本（第4题），学生对于从不同总体分别抽取一个球再组合样本的情况（第5题）更易于构建精确的样本空间．

3.3 11—14岁学生可能性比较认知水平的个体差异

研究同时考察了影响个别差异的各种可能因素，如学校类型、被试性别、家庭背景情况（父母学历、父母职业）．又由于第1、2题各年龄平均水平均接近基于精确的样本空间水平，故主要研究第3、4、5题的情况．

以学校类型（城市、城乡、农村）为自变量，以“‘摸出两个球’情境下的可能性比较水平”为因变量，进行单因素方差分析，结果表明，F学校(2, 440)=4.353，P<0.05．表明，不同学校之间“摸出两个球情境下”的可能性比较水平存在显著性差异，进一步的多重比较显示：城市地区学校和城乡结合地区学校、城市地区学校和农村地区学校学生的可能性比较水平均存在显著差异．

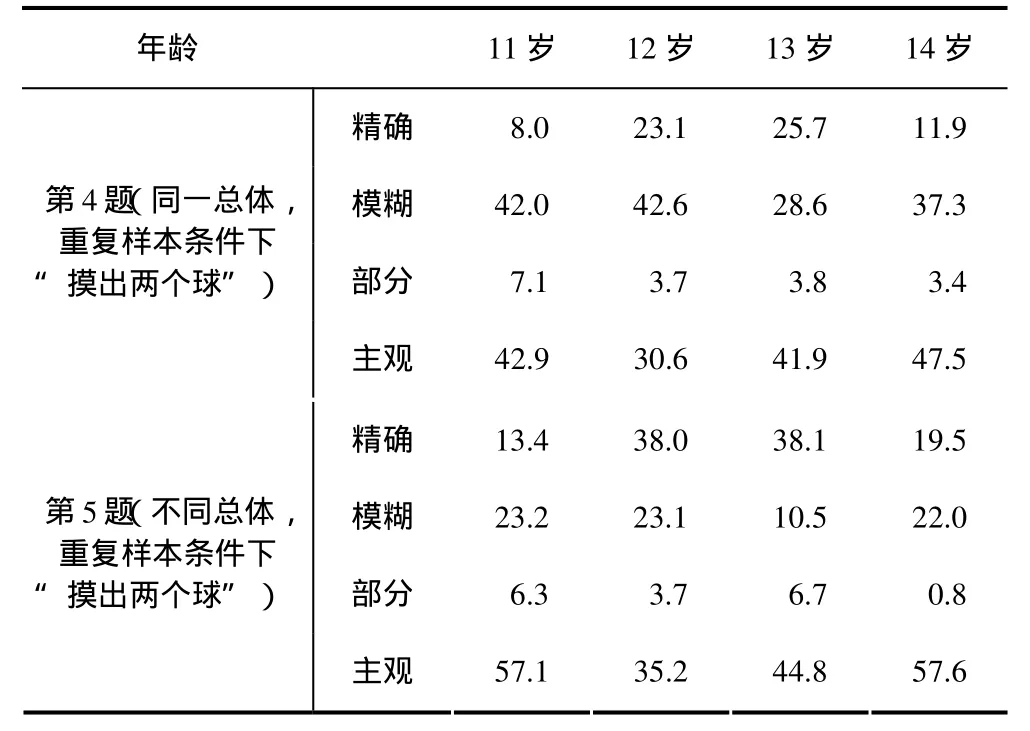
表4 各地区学校学生第4第5两题学生各水平百分比

分别以爸爸学历、妈妈学历为自变量，以学生第3、4、5题平均水平为因变量，进行方差分析．结果表明，Welch爸爸学历(4, 72.310)=6.532，P<0.001，表明爸爸的不同学历之间有着显著性差异．进一步的多重比较表明，小学、初中与大学、研究生之间有着显著性差异，其它之间差异不显著．Welch妈妈学历(4, 76.147)=6.562，P<0.001，表明妈妈的不同学历之间有着显著性差异．进一步的多重比较表明，初中与大学、研究生之间有着显著性差异，其它之间差异不显著．

考察父母不同职业学生可能性比较水平的差异，进行方差分析，

表示通过方差齐性检验．方差分析表明：F爸爸职业=1.696，Sig=0.139；F妈妈职业=1.794，Sig=0.133，表明父母的不同职业学生的可能性比较水平无显著差异．

考察不同性别学生可能性比较水平的差异，进行方差分析，Levene性别(1, 211)=3.296，P=0.071，表示通过方差齐性检验．方差分析表明：F性别=1.926，Sig=0.167，表明不同性别学生的可能性比较水平无显著差异．

综上分析表明：学生关于可能性的比较水平存在学校类型的显著差异，城市地区的学生其可能性比较水平高于城乡结合地区和农村地区的学生；从学历角度，低学历家庭背景（小学、初中）与高学历家庭背景（大学、研究生）之间存在显著性差异；父母职业背景之间的差异不显著；学生性别之间的差异不显著．

4 讨 论

4.1 11—14岁学生可能性比较认知水平的发展趋势和特点

研究根据被试解决可能性大小比较的问题时是否基于样本空间、基于什么样的样本空间，区分出被试可能性比较的4个水平，并以此为依据考察11—14岁学生可能性比较水平的发展趋势和特点．

研究发现，学生在11—12岁阶段关于可能性认知，处于缓慢发展阶段；12—13岁，处于倒退发展阶段；13—14岁，处于停滞发展阶段；对于单一样本可能性的比较，11岁学生基本能够达到较高水平；对于需要组合知识解决的可能性大小的比较，学生的平均水平明显下降，说明学生的组合知识是可能性比较能力的一个影响因素．特别地，在“摸出两个球”情境下，重复样本干扰学生构造样本空间，学生倾向于构造模糊的样本空间甚至主观判断；较之于同一总体，不同总体条件下“摸出两个球”更易构造样本空间．

4.2 11—14岁学生可能性比较认知水平发展中的个体差异

学生的可能性比较水平存在学校类型的差异，并且城市地区学校的学生总体水平高于城乡结合地区和农村地区的学生，这反映了教师的素质、教学条件对于学生学习的重要影响．基于此，研究者通过对中小学各段教材概率部分的研究，发现尽管教材中涉及生活中的概率实例，但这些实例大部分来自于城市生活，对于农村地区学生来说，很难做到联系实际．

父母的学历是影响学生可能性比较水平的影响因素，低学历家庭背景（小学、初中）与高学历家庭背景（大学、研究生）之间存在显著性差异；父母职业背景之间的差异不显著；学生性别之间的差异不显著．这说明较优越的家庭教育质量可能对学生随机认识、概率思维的发展有一定的促进作用．

4.3 学生在可能性比较过程中的典型错误认知

首先，缺乏对可能性大小的客观存在性的认识，采取主观判断的方式解决可能性大小的问题．如表4呈现的第4、5两题有近半数学生采取了主观判断．其中以下3类情况最常见：第一，一些学生认为“概率不能被预言”[5~7]，答题时选择“不知道”，给出的解释是“因为没摸之前，谁也不知道结果”，认为只有事件发生才能知道．第二，一些学生持“等可能偏见”[5~7]，答题时选“可能性一样大”，他们的解释是“每种结果都可能出现”，甚至有的学生明确指出“每种结果出现的可能性都是50%”．第三，对于第4题，相当一部分学生选择“可能性一样大”，而他们的解释是“黑球和白球一样多”．同理，第5题，相当一部分学生选择“黑白可能性大”，而他们的解释是“黑球比白球多”．诸如此类，学生试图从球的数量上解决“摸两个球”情境下的概率问题，这说明这部分学生还不能构造样本，不能基于样本空间比较事件可能性的大小．

其次，重复样本条件下倾向于构造模糊的样本空间．如表4呈现的第4、5两题有相当一部分学生只能基于模糊的样本空间判断可能性大小．比如第4题，学生给出的列举结果是“黑球、黑球，白球、白球，黑球、白球”或“黑球、黑球，白球、白球，黑球、白球，白球、黑球”．这不仅说明组合知识是可能性比较能力的一个影响因素，也表明在重复样本情境下，学生的组合知识存在困扰．

4.4 对课程标准和教材编制及课堂教学的建议

（1）对课程标准的建议．

如果以 20%左右的儿童能够掌握，作为萌芽标准；以50%左右的儿童能够掌握，作为开始理解标准；以80%左右的儿童能够掌握，作为掌握的标准[8]．那么，对于单一样本情境下的可能性比较，11岁的学生已经达到完全掌握的水平；对于需要组合知识解决的可能性比较水平的问题，学生难于摆脱重复样本的干扰，各年级均未达到理解的水平（见表 4）．因而，限于组合知识的不完备，不可以对学生概率的定量化有过高要求．基于此，《全日制义务教育数学课程标准（2011年版）》对其实验稿所做的修订，是基本合理的．

（2）组合知识先于概率量化阶段的学习，加强学生对“样本”概念的理解．

学生的组合知识是影响可能性大小比较的重要因素，这已经得到了众多研究的支撑[2，9]．Piaget还认为，两个条件对概率概念的发展很重要：一是构建排列组合运算的能力，二是建立个体案例与总体分布（本质上是样本空间）的关系的能力[2]．研究进一步表明：重复样本干扰学生组合，从而干扰学生构造精确的样本空间．新课程标准提出用实验、模拟、构造样本空间等方法计算简单等可能事件的可能性大小（概率），基于精确的样本空间判断可能性和可能性大小也就成为学生掌握概率知识的一个重要标准．基于此，组合知识一定程度上可视为学生可能性比较的“预备知识”，应先于概率知识的学习．

其次，在“概率”概念的教学中，加强学生对“样本”概念的理解尤为重要[10~11]．一方面，“样本”描述的是从所研究的对象的全体（即总体）中抽取的部分个体，而一个事件的所有样本即构成“样本空间”．许多学生之所以不能构造精确的样本空间，是因为对“样本”概念的理解偏差，比如第3题第2问：“摸出的球有几种可能的情况”，有学生回答“绿球、白球、黑球”，学生不明白该题的每一个样本（情况）包含两个球．另外，研究者还发现部分学生不能构造样本，对可能性大小进行比较时完全凭主观判断，比如第 4题的第3问，部分学生认为“可能性一样大”，给出的理由是“因为黑球和白球一样多”．另一方面，“样本”对了解总体有重要意义，即具有抽样意义，可以通过样本检验或了解总体．可见，在“概率”概念的教学中，加强“样本”概念的教学十分重要而且必要的．

（3）针对性地消除学生已有错误经验，建立正确的概率直觉．

各年级学生在不同程度上对概率的认识受到错误经验的影响．比如，一些学生选择“无法比较这两个可能性的大小”，认为“机会不能被预言和量化，机会或可能性和运气没什么差别，这种现象根本没有什么规律可循，想要度量或者预测机会或可能性是完全不可能的、毫无意义的”．还有一些学生存在“等可能偏见”，认为“随机试验的每一种可能结果都有50%的机会发生”或“每一个事件的可能性都是相同的”，这些学生虽然对随机试验的“等可能性”有一定认识，但认识是模糊不清的，往往把“等可能性”泛化，而不注意“可能结果”的划分依据的不同．逐步消除错误经验，建立正确的概率直觉是概率教学的一个重要目标．诚然，要实现这一目标，必须让学生亲自经历对随机现象的探索过程，应强调学生的亲身体验[12]．然而，不应该夸大实验（或游戏）的价值，尽量规避不必要的实验（或游戏）．比如，研究者在访谈部分持“等可能偏见”观点的学生时，试图纠正他们的错误观念，组织了一次实验：在一个不透明的盒子里放有3颗白球、两颗黑球，从中摸出一个球，摸出那种颜色球的可能性大？学生有放回地摸10次并记录结果，统计显示5次摸出的是白球，5次摸出的是黑球．学生不仅没能更正错误观念，反而加深了其“等可能偏见”的顽固性．要在“思想实验”的基础上，组织学生进行必要的实验．并且，应该明确实验（或游戏）的真正目的——不是通过实验（或游戏）来验证概率的大小，而是让学生亲历实验，从中获得数学思考、数学体验，从而修正自己的错误经验，体会随机性及随机思想，建立正确的概率直觉．

[1] 教育部．全日制义务教育数学课程标准（2011年版）[M]．北京：北京师范大学出版社，2011．

[2] Piaget J, Inhelder B. The Origin of the Idea of Chance in Children [M]. New York: Norton, 1975.

[3] Green D. Probability Concepts in 11-16 Year Old Pupils 2nd Edition [M]. Centre for Advancement of Mathematical Education in Technology, University of Technology, Loughborough, 1982.

[4] 李文玲，张厚粲．教育与心理定量研究方法与统计分析[M]．北京：北京师范大学出版社，2008．

[5] 李俊．中小学概率的教与学[M]．上海：华东师范大学出版社，2003．

[6] 李俊．关于“可能性大小无法比较”的一项调查研究[J]．数学教学，2003，（6）：28-32．

[7] 李俊．学习概率中认知的发展[J]．数学教育学报，2002，11（4）：1-5．

[8] 沈家鲜，刘范．5—17岁儿童和青少年容积概念发展的研究[J]．心理学报，1984，（2）：155-164．

[9] Fischbein E. Schemata and Intuition in Combinatorical Reasoning [M]. Educational Studies in Mathematics, 1997.

[10] 王秀军．中学生对样本概念理解的调查研究[J]．数学教育学报，2005，14（2）：71-72．

[11] 王秀军．对中学生自发抽样知识的调查研究[J]．数学教育学报，2003，12（3）：67-69．

[12] 章飞．义务教育阶段概率有关知识的内容定位与教材实施[J]．数学教育学报，2004，13（1）：48．