基于状态反馈的黄金分割控制器参数化方法及其在高超声速飞行器上的应用*

早在1963年，美国X-15高超声速飞行器以6.7马赫数在12km的高度进行了成功试飞，标志着人类对高超声速飞行器的研究进入了实质性发展阶段.在2004年，著名的X-43A高超声速飞行器突破了技术瓶颈，利用吸气式超然冲压发动机成功地将飞行器加速到10马赫，进一步增加了人们对该领域的信心.高超声速飞行器能够取代航天飞机作为地球到空间站的往返工具，也可以在地球大气层中长距离飞行.其主要优点包括：1)较航天飞机而言，具有更短的开发周期；2)较航天飞机而言，开发费用更低；3)能够在两小时内到达全球任意地点.上述优点是军事领域和民用领域所迫切需求的.但是，高超声速飞行器研究所面临的挑战是巨大的，尤其是飞行器姿态控制系统的稳定性问题[1-2].高超声速飞行器长期维持在5马赫数以上，甚至高达20马赫数的飞行速度，并且要跨越整个大气层，其气动特性变化剧烈且难以预测，而现阶段地面风洞实验难以长时间地提供可靠的测试环境.因此，在姿态控制系统设计时，对象模型和飞行环境存在非常大的不确定性，表现为非线性、参数大范围摄动和未知外界干扰.同时飞行的高速性使得姿态系统对模型参数和环境变化非常敏感.上述因素给姿态控制系统提出了巨大挑战，传统的鲁棒控制或者自适应控制难以直接适用.

近年来，大量的文献利用不同的控制方法对高超声速飞行器姿态控制系统进行了研究.针对飞行器姿态系统的非线性模型，常见的控制方法包括自适应控制[3]、鲁棒控制[4]和滑膜控制[5].考虑到姿态系统具有慢时变特性，更常见的方法是在若干个特征配平工作点进行线性化，再利用增益调度法实现控制器之间的切换.另一种方法是利用动态逆[6]或tangent线性化方法[7]，得到姿态系统的线性化模型，进而设计控制器. 也有文献将几类控制方法相融合进行控制系统的设计[8].

特征模型和黄金分割自适应控制方法由吴宏鑫院士分别于20世纪90年代和80年代提出[9-10].特征模型的基本思想是根据对象动力学特征、环境特征和控制性能要求，用一个低阶时变差分方程对系统进行建模.与降阶建模不同的是，具有低阶结构的特征模型并没有丢失高阶对象的信息，而是根据控制性能要求和对象特性，将信息合理地压缩至低阶模型中.与通常的自适应控制系统相比，基于特征模型的黄金分割自适应控制策略，具有简洁的形式，不需要在线调试，并且能够保证参数收敛过程中的稳定性，已经在卫星瞬态热流控制、空间交会对接等大量实际工程中得到了验证.近年来，这一方法还在高超声速飞行器再入过程的滑翔段[11-12]和爬升段[13]进行了应用.然而，将这一方法进一步应用于再入过程的初始段，即由再入大气层至滑翔段之前的过程中，由于大气密度和飞行环境的剧烈变化，以及飞行的高速性，使得姿态系统的瞬态响应性能不够满意，对阵风等外界扰动的抵抗能力有待提高.

针对上述问题，本文在现有的基于特征模型的黄金分割自适应控制律基础上，提出了对控制律中的变量λ进行在线自主调节的方法，不再依靠传统的经验试凑的方法，同时提高系统的H2/H∞鲁棒性能，得到的闭环系统同时具备黄金分割控制器下的自适应性和λ在线调节下的鲁棒性，因此能够适应飞行器再入过程所经受的模型参数和飞行环境的大范围变化及一定的外界干扰.

1 预备知识

用R表示实数集合.信号x(k)∈Rn,k=0,1,2,…的L2范数和L∞范数分别为

在再入过程中，高超声速飞行器通常工作于无动力状态，仅仅受到重力和气动力作用，通常采用Bolender和Doman[14]所提出的如下纵平面动力学模型进行研究：

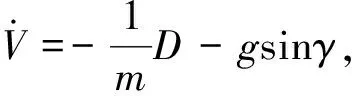
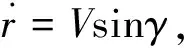
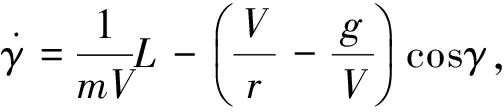
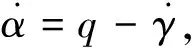
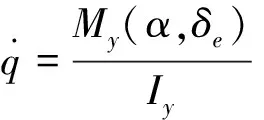
(1)

其中V,r,γ,α,q,m,My,Iy,D,L,g和δe分别为速度，地心距，飞行路径角，攻角(AOA)，俯仰角速率，飞行器质量，俯仰力矩，本体坐标下绕y轴的转动惯量，阻力，升力，重力加速度和俯仰舵偏角.

相对于攻角α，质心动力学模型中的V和r可以看作慢变量，同时，升力系数CL和阻力系数CD可以用如下2阶多项式拟合[15]：

(2)

其中MV为马赫数.由式(2)中各系数可以看出，CL和CD对攻角或速度MV不敏感.因此，当研究攻角的动力学特性时，升力L和阻力D可以看作常量.

攻角的动力学模型的相对阶为2，如下式所示：

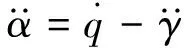
f(α,δe)

(3)

其中Sref和lref分别为参考面积和参考长度，Cmy为y轴力矩系数.

在文献[9,12,16]中已证明，在合适的采样时间δt下，如果式(3)中的非线性函数f(α,δe)满足：

1)|f(α(t+δt),δe(t+δt))|-|f(α(t),δe(t))|0；

2)f(α,δe)关于α和δe的偏导数有界；

3)f(0,0)=0.

那么有下述引理成立：

引理1.当要实现位置保持或位置跟踪控制时，在满足一定的采样周期δt下，式(3)给出的关于攻角α的动力学模型可用如下具有二阶差分方程形式的特征模型描述：

α(k+1)=f1(k)α(k)+f2(k)α(k-1)+

g0(k)δe(k)

(4)

其中g0(k)=O2(δt),且

在实际应用中，参数fi和g0是利用最小二乘法参数递推估计公式或梯度法在线辨识得到[17].

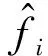
注2.为了改善闭环系统的瞬态响应，在特征模型中有时添加g1(k)δe(k-1)项，如文献[10].

引理2[22].时变系统

x(k+1)=A(k)x(k)

(5)

指数稳定，如果A(k)的特征值一致在单位圆内，A(k)有界且慢时变，其中A(k)∈Rn×n,n≥1.

2 主要结果

基于引理2可以证明，对于模型(4)及黄金分割自适应控制律

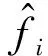
然而，目前缺少对控制器参数λ求解的可靠方法，现有的应用主要依靠经验确定λ值.但是，考虑到高超声速飞行器再入过程穿越整个大气层，模型参数变化范围较大，固定的λ可能难以适应这一变化，因此迫切需要研究控制器参数λ的在线自适应调节方法，以保证高超声速飞行器在整个再入过程的稳定性.

另一方面，考虑到大气环境的不确定性和阵风、切变风等的外界干扰，特别是50km以下稠密大气环境下气动力和气动力矩对不确定性的敏感性，控制系统的鲁棒性，特别是对抗外界干扰的能力，也是评价飞行器姿态控制系统好坏的关键指标.

基于上述分析，在式(5)给出的控制器基础上，考虑如下黄金分割鲁棒自适应控制器

(6)

在以下内容中，将着重研究参数λ(k)的求解方法，使得对一定条件下的外界扰动w(k)和参数摄动，闭环系统满足以下性能指标：

1)外界扰动w(k)对系统输出z∞(k)的传递函数Tz∞w的H∞范数满足

(7)

2)外界扰动w(k)对系统输出z2(k)的传递函数Tz2w的H2范数满足

(8)

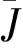
在外界扰动w(k)的作用下，特征模型改写为

α(k+1)=f1(k)α(k)+f2(k)α(k-1)+

g0(k)δe(k)+B2(k)w(k)

(9)

相应的输出为：

(10)

其中C0=C1=[0 1].系统输出z∞对应于扰动w(k)∈L2激发的H∞性能指标，输出z2对应于扰动w(k)∈L∞激发的H2性能指标.

令状态变量x1(k)=α(k),x2(k)=α(k+1),则在控制律(6)下，闭环系统具有如下状态空间表达式：

(11)

其中

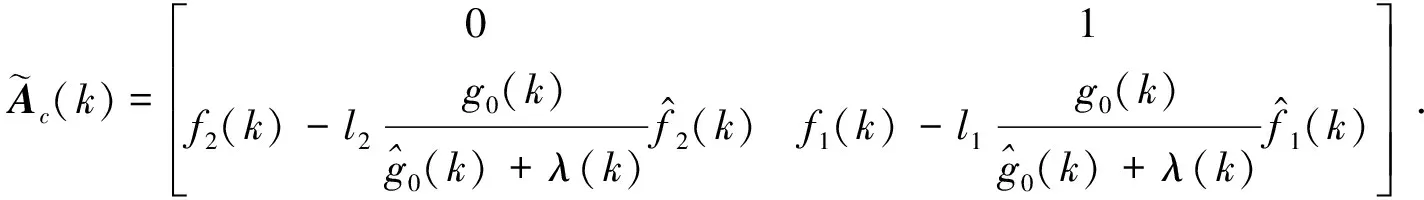
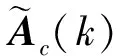
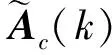
(12)

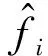
A0+B1Um+ΔA0

(13)

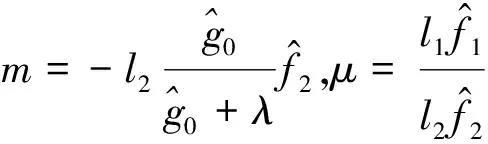
根据注释1，参数f1,f2的估计误差是关于采样时间的无穷小量，因此，不确定矩阵ΔA0是范数有界的结构化输入矩阵：

ΔA0=HFE

(14)

其中FTF≤I.不失一般性，令H=[0h],h∈R且E=eI,e∈R.

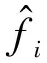
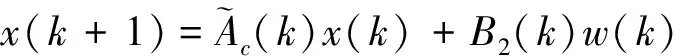
(15)

其中AC=A0+B1Um.

上述引理是文献[18]中结论的直接应用.条件(15)是双线性矩阵不等式，通常情况下可以利用一些处理手段将其转化为线性矩阵不等式形式，从而可借助Matlab工具箱进行求解[19].然而，本文所讨论的问题具有一定的特殊性，主要体现在系统矩阵Ac是关于未知变量m的仿射函数，如式(13)所示.因此，在满足黄金分割控制律这一前提下，传统的状态反馈控制增益的求解问题转化为具有结构约束[1μ]m的关于未知量m的控制增益求解问题.从而增加了求解难度，现有的处理手段无法直接适用.

将矩阵AC,E,C1,C0和H代入式(15)，基于Schur补，得到不等式(15)的等价条件如下

(16)

其中

再次对式(16)应用Schur补，得到等价条件为

G<0，G-(-p3+hβ)-1(v1+mv2)(v1+mv2)T<0

(17)

其中G是矩阵M左上方的4×4对角块且

(18)

考虑不等式

G-(-p3+hβ)-1(v1+mv2)(v1+mv2)T-ZΛZT<0

(19)

或等价的

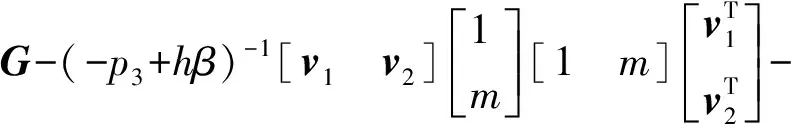
ZΛZT<0

(20)

上述不等式成立的充分条件为：

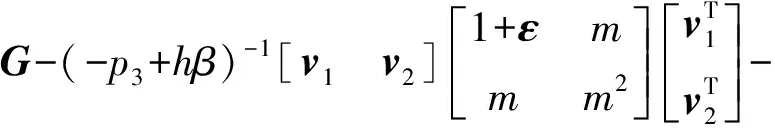
ZΛZT<0

(21)

其中，ε的引入是为了避免出现奇异矩阵.

因此，式(21)或等价的条件(16)成立的充分条件是

其中

(22)

从式(22)中可以看出，等式左边未知变量个数大于等式右边未知变量个数，因此直接求解可能出现无解，下面给出对上述问题的一种解决方法.

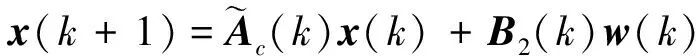
Y1+(-p3+hβ)-Y3m2<0

(23)

证明.证明过程可参考文献[20]，因篇幅限制，在此略去.

条件(23)是线性矩阵不等式，可以利用LMI-toolbox进行计算.为了降低其保守性，可考虑如下优化问题：

min(Y1-Y2-Y3-p3-β)

s.t.(23)成立.

推论3.根据引理2，对于特征模型(9)和控制律(6)组成的闭环系统渐进稳定，且H2和H∞性能指标满足要求的充分条件是，在每一个采样时间内，控制器参数λ(k)满足定理3.

4 高超声速飞行器再入过程的姿态控制

为了体现本文提出的鲁棒自适应控制律对飞行环境大范围变化的适应能力，在仿真中将飞行器的初始高度设定为43km，初始速度为2.5km/s.假设气动参数的不确定性为具有cosine形式的表达式:ΔCm·=±0.3cos(0.05Cm·).在t=3s时，设攻角受到外界扰动使其偏离指令角3°.根据定理3，在每一个采样周期计算控制器参数λ(k)，计算结果如图1所示，相应的高度和速度的变化曲线如图2所示.攻角的指令角为10°，其跟踪曲线如图3所示.其中，实线、点线和虚线分别对应λ(k),λ=0.01和λ=0.000001时的动态响应曲线.在外界扰动作用下，攻角跟踪误差的H2范数和H∞范数的计算结果如表格1所示.通过对仿真数据的比较可知，引入λ(k)在线优化的思想，闭环系统具有更小跟踪误差和更强的抗扰能力，从而验证了本文所提出方法的有效性和适用性.

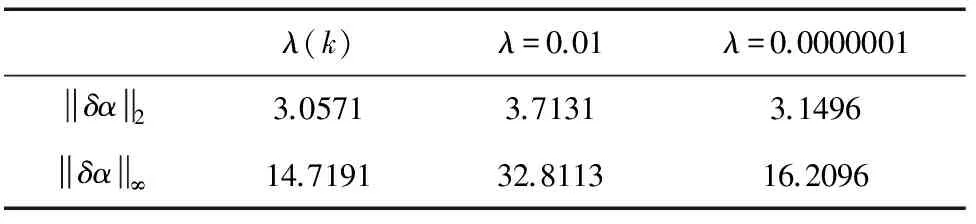
表1 攻角跟踪误差的H2范数和H∞范数

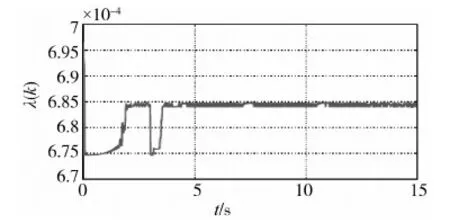
图1 λ(k)的计算结果

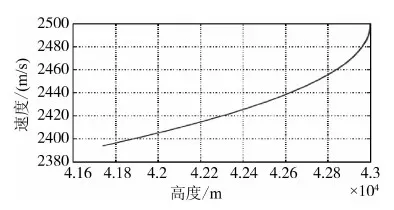
图2 再入轨迹

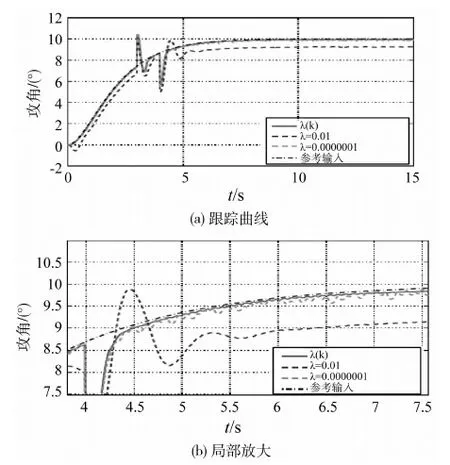
图3 不同的λ对应的攻角跟踪曲线

5 结 论

本文主要研究具有大升阻比的高超声速飞行器再入过程的鲁棒自适应姿态控制方法.针对再入过程环境大范围变化，在现有的基于特征模型的黄金分割自适应控制方法基础上，提出了基于线性矩阵不等式的控制器参数λ(k)的求解方法，改进后的控制律中λ(k)通过在线实时计算得到，且计算效率高，在保证系统稳定性的前提下，提高了瞬态响应性能和抵抗外界干扰的鲁棒性.通过仿真验证了算法的优越性、适应性和有效性.

参 考 文 献

[1]Fidan B , Mirmirani M, Ioannou P A , Flight dynamics and control of air-breathing hypersonic vehicles: review and new directions[C]. The 12thAIAA International Space planes and Hypersonic Systmes and Technologies, Norfolk, Virginia, 2003

[2]Huang L, Duan Z S, Yang J Y. Challenges of control science in near space hypersonic aircrafts[J]. Control Theory & Applications, 2011, 28(10): 1496-1505

[3]Lind R. Linear parameter-varying modeling and control of structural dynamics with aerothermoelastic effects[J].Journal of Guidance Control and Dynamics,2002， 25: 733-739

[4]Fiorentini L, Serrani A, Michael A B. Nonlinear robust/adaptive controller design for an air-breathing hypersonic vehicle model[C]. AIAA Guidance, Navigation and Control Conference and Exhibit, South Carolina, USA, 2006

[5]Xu H J, Mirmirani M D, Ioannou P A. Adaptive sliding mode control design for a hypersonic flight vehicle[J]. Journal of Guidance, Control, and Dynamics, 2004, 27(5): 829-838

[6]Brinker J S, Wise K A. Flight testing of reconfigurable control law on the X-36 tailless aircraft[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(5): 903-909

[7]Cai G B, Duan G R, Hu C H,et al. Tracking control for air-breathing hypersoinc cruise vehicle based on tangent linearization approach[J]. Journal of Systems Engineering and Electronics, 2010, 21(3): 469-475

[8]Reiman S E, Dillon C H, Lee H P, et al.Adaptive reconfigurable dynamic inversion control for a hypersonic cruise vehicle[C]. AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, Hawaii, August 2008

[9]Meng B,Wu H X. A unified proof of the characteristic model of linear time-invariant systems[C]. American Control Conference, New York, USA, 2007

[10]Wu H X, Hu J, Xie Y C. Characteristic model-based all-coefficient adaptive control method and its applications[J]. IEEE Transactions on Systems, Man, and Cybernetics-Part C: Applications and Reviews, 2007, 37(2): 213-221

[11]Luo X,Li J. Fuzzy dynamic characteristic model based attitude control of hypersonic vehicle in gliding phase[J]. Science China: Series F Information Sciences, 2011, 54(3): 448-459

[12]孟斌, 吴宏鑫, 高超声速飞行器基于特征模型的自适应控制[C]. 第26届中国控制会议,张家界，2007

Meng B,Wu H X. Adaptive control based on characteristic model for a hypersonic flight vehicle[C]. The 26thChinese Control Conference, Zhangjiajie, 2007

[13]Meng B, Wu H X, Lin Z L. Characteristic model based control of the X-34 reusable launch vehicle in its climbing phase[J].Science China: Series F Information Sciences, 2009,52:2216-2225

[14]Bolender M A, Doman D B. A nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J]. Journal of Spacecraft and Rockets, 2007, 44(2): 374-387

[15]Bollino K P. High-fidelity real-time trajectory optimization for reusable launch vehicles[D]. Naval Postgraduate School, 2006

[16]吴宏鑫, 胡军, 解永春. 基于特征模型的智能自适应控制[M].北京：中国科学技术出版社, 2009

[17]Qi C, Wu H, Lv Z. The study on the stability of all-coefficient golden section feedback control system[C]. The 3rdWorld Congress on Intelligent Control and Automation, Hefei, 2000

[18]Bernstein D S, Haddad W M. LQG control withH∞performance bound: a Riccati equation approach[J]. IEEE Transactions on Automatic Control, 1989, 34(3): 293-305

[19]Boyd S, Ghaoui L E, Feron E, et al. Linear matrix inequalities in system and control theory[M].Philadelphia: Society for Industry and Applied Mathematics, 1994

[20]Huang H，Wang Y. MixedH2/H∞robust adaptive control of hypersonic vehicles based on the characteristic model[C]. Chinese Control Conference, Hefei, 2012

[21]郭雷, 时变随机系统—稳定性、估计与控制[M].长春： 吉林科学技术出版社, 1993