相空间中类分数阶变分问题的Noether对称性与守恒量

张 毅

(苏州科技学院 土木工程学院，江苏 苏州 215009)

分数阶微积分为科学和工程的不同领域的大量问题提供了一个强有力的数学工具，并在数学物理，经典和量子力学，控制理论，非线性动力学，信号与图像处理，热力学，以及生物工程等领域取得了许多突破性的成果[1-5]。尽管分数阶微积分在许多领域的应用已经确立，但是在其它一些领域的应用研究还刚刚开始，分数阶变分问题及其对称性和守恒量的研究就是后者的一个例子。

为了建立非保守动力学系统模型，El-Nabulsi于2005年提出了一种新的建模方法[24]，即：类分数阶变分方法或可称之为El-Nabulsi分数阶模型。在类分数阶变分方法中，分数阶时间积分仅引进一个实参数α，所得到的Euler-Lagrange方程形式简单且类似于经典的方程。该Euler-Lagrange方程的新颖之处在于存在一个作用在系统上的广义分数阶外力。尤其是在所得到的方程中不出现分数阶导数，而仅仅依赖于分数阶积分的阶α。最近，类分数阶变分方法被进一步推广到Lagrange函数依赖于Riemann-Liouville分数阶导数情形[25]，多维类分数阶变分问题[26]，受完整约束或非完整约束或耗散动力学系统的类分数阶变分问题[27]，按指数规律变化的类分数阶变分问题[28]，并通过引入广义分数阶导数算子给出了普适的类分数阶Euler-Lagrange方程[29]。Frederico和Torres研究了类分数阶变分问题的运动常数，基于El-Nabulsi分数阶模型给出非保守系统的Noether定理[35]，并推广到Lagrange函数含有高阶导数情形[36]，但是由于文中关于Noether准对称性的概念有误，因此所得到的Noether定理是不正确的。

本文在类分数阶变分方法的框架下进一步研究相空间中类分数阶Noether理论。通过求解相空间中类分数阶变分问题，得到了类分数阶Hamilton正则方程；给出了相空间中类分数阶Hamilton作用量变分的两个基本公式，提出了相空间中类分数阶Noether对称变换和准对称变换的定义和判据；建立了类分数阶Hamilton系统的Noether定理，并举例说明结果的应用。

1 类分数阶变分问题

假设力学系统的位形由n个广义坐标qk(k=1,2,…,n)来确定，其所受的约束是理想、完整的，系统的广义动量和Hamilton函数为

(1)

式中L为Lagrange函数。根据El-Nabulsi提出的分类阶动力学建模方法[24]，相空间中类分数阶变分问题可定义如下：

求积分泛函

(2)

在给定边界条件

qk(a)=qk,a,qk(b)=qk,b(k=1,2,…,n)

(3)

上述变分问题可称为相空间中类分数阶变分问题，泛函(2)可称为相空间中类分数阶Hamilton作用量。

根据变分学理论，泛函(2)在qk=qk(τ)，pk=pk(τ)上取得极值的必要条件是其变分等于零，即δS=0，于是有

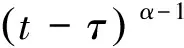
(4)

由于

(5)

由边界条件(3)，得到

δqk|τ=a=δqk|τ=b=0 (k=1,2,…,n)

(6)

利用式(5)和(6)，式(4)给出

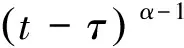
(7)

将式(1)的第二式两边对pk求偏导数，有

(8)

将式(8)代入式(7)，并由δqk的独立性和积分区间的任意性，得

(9)

联合方程(8)和(9)，构成类分数阶Hamilton正则方程[24]，即

(10)

我们称由方程(10)描述的力学系统为类分数阶Hamilton系统。如取α=1，方程(10)给出经典的Hamilton正则方程。

2 类分数阶Noether对称性

引进无限小r参数有限变换群

(11)

或其展开式

(k=1,2,…,n)

(12)

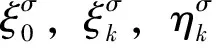
(13)

于是有

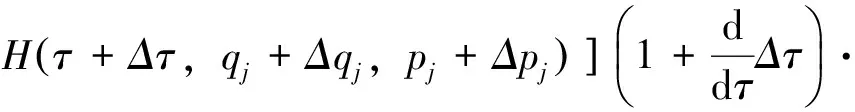
(14)

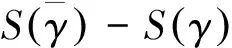
(15)

根据非等时变分Δ与等时变分δ之间的关系式[37]

(16)

其中F为任意可微函数，可以得到

(17)

由式(17),式(15)可表为

(18)

由式(12)，式(18)可进一步表为

(19)

式(15)和(19)是相空间中类分数阶Hamilton作用量变分的两个基本公式。

下面，我们给出相空间中类分数阶Noether对称变换的定义和判据。

定义1 如果相空间中类分数阶Hamilton 作用量(2)是无限小群变换(11)的不变量，即对每一个无限小变换，始终成立

ΔS=0

(20)

则称无限小群变换为相空间中类分数阶Noether对称变换。

由定义1和公式(15)，可得到如下判据1。

判据1 对于无限小群变换(11)，如果满足条件

(21)

则变换是相空间中的类分数阶Noether对称变换。

条件(21)也可表示为

(σ=1,2,…,r)

(22)

当取r=1时，式(22)可称为相空间中的类分数阶Noether等式。

利用判据1可以判断所论系统的类分数阶Noether对称性。

其次，研究相空间中的类分数阶Noether准对称变换。

设H′是另外的Hamilton函数，如果变换(11)精确到一阶小量满足条件

(23)

则称类分数阶Hamilton作用量(2)是无限小群变换(11)下的准不变量。由此确定的H′与H具有同样的运动微分方程，则变换称为相空间中类分数阶Noether准对称变换。此时有

(24)

将式(24)代入式(23)，我们有

(25)

式(25)中G应为一阶小量，故可用ΔG来代替G。

于是有

定义2 如果相空间中类分数阶Hamilton作用量(2)是无限小群变换(11)的准不变量，即对每一个无限小变换，始终成立

(26)

则称无限小群变换为相空间中类分数阶Noether准对称变换。

由定义2和公式(15)，可以得到如下判据2。

判据2 对于无限小群变换(11)，如果满足条件

(27)

则变换是相空间中的类分数阶Noether准对称变换。

条件(27)也可表为

(σ=1,2,…,r)

(28)

其中ΔG=εσGσ.当取r=1时，式(28)可称为相空间中的类分数阶广义Noether等式。

利用判据2，可以判断所论系统的类分数阶Noether准对称性。

3 类分数阶Noether对称性导致的守恒量

首先，给出类分数阶Hamilton系统的守恒量的定义。

定义3 函数I(τ,q,p)称为类分数阶Hamilton系统的守恒量，当且仅当沿着类分数阶Hamilton正则方程(10)的解曲线恒成立

(29)

对于类分数阶Hamilton系统，如果能找到相空间中类分数阶Noether对称变换或准对称变换，便可求得与之相应的守恒量。有如下定理。

定理1 对于类分数阶Hamilton系统(10)，如果无限小群变换(12)是系统的类分数阶Noether对称变换，则系统存在r个线性独立的守恒量，形如

(σ=1,2,…,r)

(30)

证明因无限小群变换(12)是系统的类分数阶Noether对称变换，由定义1，有

ΔS=0

(31)

将式(19)代入上式，得

(32)

将方程(10)代入上式，由εσ的独立性和积分区间[a,b]的任意性，得到

(33)

积分之，便得式(30)。证毕。

定理2 对于类分数阶Hamilton系统(10)，如果无限小群变换(12)是系统的类分数阶Noether准对称变换，则系统存在r个线性独立的守恒量，形如

(σ=1,2,…,r)

(34)

证明由定义2和方程(10)，类似于定理1，可容易证明之。

定理1和定理2称为相空间中类分数阶Noether定理。定理表明，如果能找到所论系统的类分数阶Noether对称变换或类分数阶Noether准对称变换，便能求出系统的守恒量。

4 算 例

例已知二自由度系统的Lagrange函数为

(35)

试研究其类分数阶Noether对称性和守恒量。

由式(1)知

(36)

类分数阶广义Noether等式(28)给出

(37)

方程(37)有解

(38)

(39)

(40)

由本文判据，生成元(38)相应于系统的类分数阶Noether对称变换，生成元(39)，(40)相应于系统的类分数阶Noether准对称变换。由本文定理，对应于生成元(38)，(39)和(40)，守恒量式(34)分别给出为

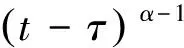
(41)

(42)

I3=0

(43)

其中式(43)表示与式(40)对应的无限小变换是平庸的。

5 结 语

利用分数阶微积分进行非保守力学系统或耗散系统的动力学建模，可以解决用经典微积分方法建立起来的模型所难以解决的问题[4, 6-7]。基于El-Nabulsi提出的分数阶模型，文章研究了相空间中的分数阶变分问题，建立了分数阶模型下的Hamilton正则方程。在El-Nabulsi分数阶模型的框架下，将经典的Noether对称性理论推广到分数阶系统，建立了相空间中的分数阶Noether理论，从而在更一般意义上揭示了动力学系统的对称性与守恒量之间的内在联系。本文的方法和结果具有普遍意义，可进一步推广应用于各类约束力学系统，并且经典的Noether定理是本文的特例。

参考文献：

[1] OLDHAM K B, SPANIER J. The fractional calculus [M]. San Diego: Academic Press, 1974.

[2] MILLER K S, ROSS B. An introduction to the fractional integrals and derivatives-theory and applications[M]. New York: John Wiley and Sons Inc, 1993.

[3] PODLUBNY I. Fractional differential equations [M]. San Diego: Academic Press, 1999.

[4] HILFER R. Applications of fractional calculus in physics [M]. Singapore: World Scientific, 2000.

[5] KILBAS A A, SRIVASTAVA H M,TRUJILLO J J. Theory and applications of fractional differential equations[M]. Amsterdam: Elsevier B V, 2006.

[6] RIEWE F. Nonconservative lagrangian and hamiltonian mechanics[J]. Phys Rev E, 1996, 53(2): 1890-1899.

[7] RIEWE F. Mechanics with fractional derivatives [J]. Phys Rev E, 1997, 55(3): 3581-3592.

[8] KLIMEK M. Fractional sequential mechanics-models with symmetric fractional derivative [J]. Czechoslovak J Phys, 2001, 51(12): 1348-1354.

[9] KLIMEK M. Lagrangian and hamiltonian fractional sequential mechanics [J]. Czechoslovak J Phys, 2002, 52(11): 1247-1253.

[10] AGRAWAL O P. Formulation of euler-lagrange equations for fractional variational problems [J]. J Math Anal Appl, 2002, 272(1): 368-379.

[11] AGRAWAL O P. Fractional variational calculus and the transversality conditions [J]. J Phys A: Math Gen, 2006, 39: 10375-10384.

[12] AGRAWAL O P. Fractional variational calculus in terms of Riesz fractional derivatives [J]. J Phys A: Math Theor, 2007, 40(24): 6287-6303.

[13] AGRAWAL O P, MUSLIH S I, BALEANU D. Generalized variational calculus in terms of multi-parameters fractional derivatives [J]. Commun Nonlinear Sci Numer Simulat, 2011, 16(12): 4756-4767.

[17] JUMARIE G. Fractional Hamilton-Jacobi equation for the optimal control of nonrandom fractional dynamics with fractional cost functions [J]. J Appl Math & Computing, 2007, 23(1-2): 215-228.

[18] BALEANU D, AVKAR T. Lagrangians with linear velocities within Riemann-Liouville fractional derivatives [J]. Nuovo Cimento B, 2003, 119(1): 73-79.

[19] BALEANU D, TRUJILLO J I. A new method of finding the fractional Euler-Lagrange and Hamilton equations within Caputo fractional derivatives [J]. Commun Nonlinear Sci Numer Simulat, 2010, 15: 1111-1115.

[20] BALEANU D, MUSLIH S I, RABEI E M et al. On fractional Hamiltonian systems possessing first-class constraints within Caputo derivatives [J]. Romanian Reports in Physics, 2011, 63(1): 3-8.

[21] ALMEIDA R, TORRES D F M. Necessary and sufficient conditions for the fractional calculus of variations with Caputo derivatives [J]. Commun Nonlinear Sci Numer Simulat, 2011, 16: 1490-1500.

[22] ODZIJEWICZ T, MALINOWSKA A B, TORRES D F M. Fractional variational calculus with classical and combined Caputo derivatives [J]. Nonlinear Analysis, 2011, doi:10.1016/j.na.2011.01.010.

[23] MALINOWSKA A B, TORRES D F M. Generalized natural boundary conditions for fractional variational problems in terms of the Caputo derivative [J]. Comput Math Appl, 2010, 59: 3110-3116.

[24] EL-NABULSI A R. A fractional approach to nonconservative Lagrangian dynamical systems [J]. Fizika A, 2005, 14(4): 289-298.

[25] EL-NABULSI A R. Necessary optimality conditions for fractional action-like integrals of variational calculus with Riemann-Liouville derivatives of order (a,b) [J]. Math Methods Appl Sci, 2007, 30: 1931-1939.

[26] EL-NABULSI A R,TORRES D F M. Fractional action-like variational problems [J]. J Math Phys, 2008, 49:053521.

[27] EL-NABULSI A R. Fractional action-like variational problems in holonomic, non-holonomic and semi-holonomic constrained and dissipative dynamical systems [J]. Chaos, Solitons and Fractals, 2009, 42: 52-61.

[28] EL-NABULSI A R. Fractional variational problems from extended exponentially fractional integral [J]. Applied Mathematics and Computation, 2011, 217: 9492-9496.

[29] EL-NABULSI A R. Universal fractional Euler-Lagrange equation from a generalized fractional derivate operator [J]. Central European Journal of Physics, 2011, 9 (1): 250-256.

[30] CRESSON J. Fractional embedding of differential operators and Lagrangian systems [J]. Journal of Mathematical Physics, 2007, 48: 033504.

[31] RABEI E M, NAWAFLEH K I, HIJJAWI R S, et al. The Hamilton formalism with fractional derivatives [J]. J Math Ahal Appl, 2007, 327: 891-897.

[32] RABEI E M, ABABNEH B S. Hamilton-Jacobi fractional mechanics [J]. J Math Anal Appl, 2008, 344: 799-805.

[33] RABEI E M, RAWASHDEH I M, MUSLIH S,et al. Hamilton-Jacobi formulation for systems in terms of Riesz’s fractional derivatives [J]. Int J Theor Phys, 2011, 50: 1569-1576.

[34] TARASOV V E. Fractional dynamics[M]. Beijing: Higher Education Press, 2010.

[35] FREDERICO G S F, TORRES D F M. Constants of motion for fractional action-like variational problems [J]. Int J Appl Math, 2006, 19(1): 97-104.

[36] FREDERICO G S F, TORRES D F M. Non-conservative Noether’s theorem for fractional action-like variational problems with intrinsic and observer times [J]. Int J Ecol Econ Stat, 2007, 9(F07): 74-82.

[37] MEI F X, WU H B. Dynamics of constrained mechanical systems[M]. Beijing: Beijing Institute of Technology Press, 2009.