股指期货波动率的半参数预测模型及其MCS检验
2013-04-24田凤平
杨 科,田凤平
(1.华南农业大学经济管理学院,广东 广州 510642;2.中山大学国际商学院,广东 广州 510275)
股指期货作为以股票指数为标的资产的特殊金融衍生品,具有价格发现、套期保值和市场调节等多重市场功能,现已发展为国际资本市场上最为活跃的金融衍生品。作为我国唯一上市的金融期货产品——沪深300股指期货的正式上市交易,进一步完善了我国的资本市场结构,增加了我国资本市场的流动性和有效性,在我国资本市场价格发现和风险防范过程中扮演着越来越重要的角色。然而,股指期货是一柄“双刃剑”,在为资本市场提供风险管理工具的同时亦难以摆脱衍生产品固有的高风险特性。由于采用的是保证金交易、逐日盯市以及强行平仓制度等,期货价格的波动会造成投资者获利和损失成倍放大,其市场风险远远高于股票现货交易,使用不当极易诱发资本市场风险乃至金融危机。因此,准确刻画和预测股指期货市场波动率对投资者有效规避投资风险以及管理层科学合理发挥股指期货的市场调节功能,最终促进资本市场平稳较快发展具有重要的理论价值和现实意义。
自从Engle的ARCH模型[1]、Bollerslev的GARCH模型[2]以及Taylor的随机波动率模型[3]开创以来,GARCH类模型和随机波动率类模型在股指期货等各类金融资产收益的波动率估计和预测中的主导地位逐渐得到广泛的认可,这两类模型至今仍然不断获得扩展和改进。但是,这些模型都是利用低频收益率数据来估计和预测金融资产波动率,损失了大量的日内交易信息,对波动率的估计和预测存在较大的偏差,并且这些模型在处理多维问题和矩估计有效性方面存在着难以克服的缺陷。近年来,随着电子化交易的普及和信息存储技术的发展,以高精度时间“分”、“秒”为刻度来存储信息的高频环境逐步建立,并开始成为股指期货等各类金融资产价格波动度量以及预测研究的重点和热点。高频数据可以迅速有效地捕捉市场信息,比低频数据更能反映金融市场的真实状况。以Anderson等[4-8]为代表的一些国外学者提出基于金融资产高频数据的已实现波动率(Realized Volatility,RV)的方法。该方法可以获得更加准确的波动率估计值,并且不需要建立模型,也不需要进行复杂的参数估计,而且还可以将已实现波动率看成一个已观测到的时间序列(在GARCH类模型和随机波动率类模型中波动率都是潜在的,无法直接观察到),以此为基础,金融资产收益波动率的估计、建模和预测研究大为拓展。
在高频数据的已实现波动率预测建模方面,最为经典的两类模型是Andersen等[8]构建的对数已实现波动率的ARFIMA模型和Corsi[9]基于异质市场假说和HARCH模型的思想构建的HAR模型。Andersen等[8]研究发现,基于高频数据的ARFIMA模型的样本外预测能力比基于低频数据的长记忆参数模型FIGARCH模型、FIEGARCH模型以及其他相关的方法的样本外预测能力好。Corsi[9]通过Monte Carlo模拟和实证检验发现,HAR模型对已实现波动率的样本外预测能力与ARFIMA模型极为相近,并且该模型估计方法更为简便。在ARFIMA模型的基础上,国内学者对基于高频数据的已实现波动率预测建模方面,也做了一些研究,例如,郭名媛等[10]基于赋权已实现波动率建立的ARFIMA模型进一步提高了波动率的预测精度。魏宇等[11]实证比较了对数已实现波动率的ARFIMA模型与随机波动率模型、GARCH模型对中国股市波动率的预测精度,他们的研究结果发现,对数已实现波动率的ARFIMA模型对我国股市波动率的预测精度要明显高于随机波动率模型和GARCH模型。魏宇[12]基于多分形波动率(Multifractal Volatility),构建了多分形波动率的ARFIMA模型,并运用SPA检验法,实证比较了多分形波动率模型与现有的如已实现波动率模型、GARCH模型以及随机波动率模型对市场波动率预测能力的优劣。在股指期货波动率研究方面,Areal等[13]以及Xie等[14]分别采用已实现波动率和传统历史波动率方法对美国等地股指期货波动率进行了刻画,国内魏宇[15]以沪深300股指期货仿真交易的5分钟高频数据为例,运用滚动时间窗的样本外预测和SPA检验,比较了基于日收益数据的历史波动率模型和基于高频数据的已实现波动率模型对波动率的刻画和预测能力。
然而,ARFIMA模型和HAR模型及其扩展模型一般是建立在扰动必须服从正态分布且不存在条件异方差的假设下。通过对沪深300股指期货日已实现波动率的分析,笔者发现尽管对数已实现波动率的分布比RV本身更加近似于正态分布,但在所有标准的显著水平上都拒绝为正态,虽然已实现波动率的对数转换能够部分消除条件异方差,但仍然存在条件异方差的证据。因此,用ARFIMA模型和HAR模型来预测股指期货市场的波动率是不精确的,可以通过不设定扰动项的具体分布形式以及去异方差的转换等方式得到进一步改善。
鉴于此,为了克服现有文献存在的缺陷, 本文在Barndorff-Nielsen等[16-17]的线性非负模型的基础上,运用Yu等[18]的建模思想,首先对已实现波动率进行幂转换,然后不设定非负扰动部分的相关结构以及扰动项的具体分布形式,构建了一个股指期货市场波动率的半参数预测模型。该模型采用基于极值估计量的两阶段估计法进行估计,本文中还进一步探讨了模型参数估计量的渐进性质并设计两个Monte Carlo模拟实验考察模型参数估计方法的效果。最后,本文还运用最新发展起来的MCS(Model Confidence Set)检验,在多种稳健损失函数下,评价和比较了新建立的半参数预测模型和其他波动率预测模型对沪深300股指期货已实现波动率的预测能力。
1 模型与研究方法
1.1 股指期货波动率的高频估计

(1)
由于股指期货市场不是24小时连续交易,能观察到和记录的高频交易数据只能反映有交易时段的市场波动状况,而无法包含无交易时段的市场波动信息,因此,式(1)所述的已实现波动率估计量是市场真实波动率的有偏估计量。为了考虑股指期货市场休市期间的波动状况,本文采用Martens[20]的尺度参数δ对式(1)所述的估计量进行偏差修正,修正后的已实现波动率估计量可以表述为
(2)

1.2 半参数预测模型
Barndorff-Nielsen等[16]基于波动率的连续时间模型构建的线性非负模型和Yu等[18]通过Box-Cox转换代替对数转换扩展Taylor[3]的随机波动率模型而得到的Box-Cox模型对波动率建模很有用,但尚未有文献讨论其在已实现波动率预测方面的用处。此外,这两个模型各自都存在缺陷:线性非负模型需假设扰动项是独立同分布序列,因此该模型不容许有条件异方差,而Box-Cox模型则面临“截取问题”。
本文首先将Yu等[18]的Box-Cox模型转换为已实现波动率RVt的形式
h(RVt,λ)=α+βh(RVt-1,λ)+εt,t=2,…,T
(3)

(4)
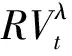
RVt=(α+1)+β(RVt-1-1)+εt
(5)
当λ=0时模型(4)常见的对数-线性高斯AR(1)模型(后文记为lnRV-LinAR模型)
lnRVt=α+βlnRVt-1+εt
(6)
与lnRV-LinAR模型相比,模型(4)更具有一般性,但存在两个缺陷:① 该模型的右边必须为非负数,与正态分布的支撑是整个实数域相矛盾;② 该模型对已实现波动率的幂转换强加了一个AR(1)结构,而Andersen和Bollerslev等[8]的研究发现波动率的真实动态特征比AR(1)结构更复杂,例如,AR(1)结构无法捕获波动率的长记忆性。
鉴于模型(4)的缺陷,本文结合Barndorff-Nielsen等[16]线性非负模型的思想,构建了下面形式的半参数模型
(7)
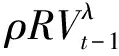
1.3 模型的估计及预测
若λ已知,可以采用极值估计量(Extreme Value Estimator)来估计半参数模型(7)的参数ρ
(8)
文献中已经证明,当模型(7)的扰动项为独立同指数分布的随机变量时,式(8)所示的极值估计量也是参数ρ的极大似然估计量[21]。类似于OLS估计量,极值估计量的一致性也不需要假定扰动项服从一个具体分布,但极值估计量在ρ<1时的收敛速度比OLS估计量快,并且极值估计量的一致性的存在条件不涉及任何高阶矩的存在性。
由于在实证研究中,参数λ是未知的,因此本文运用基于极值估计量的两阶段估计法来同时估计模型(7)的参数ρ和λ。具体步骤如下:
(9)
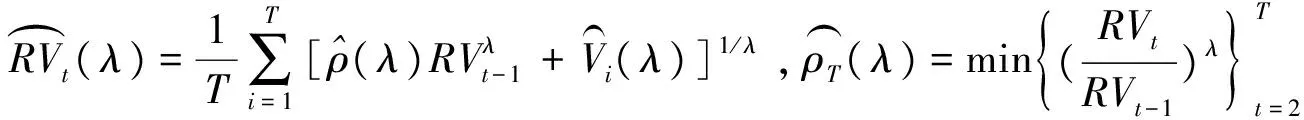
第二步,运用极值估计法来估计参数ρ
(10)
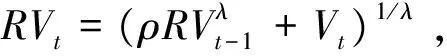
本文估计参数λ采用的是最小化向前一步预测误差的平方和,也可采用最小化向前一步预测误差的绝对值和,但通过模拟实验以及大量的实证研究,发现采用最小化向前一步预测误差平方和对股指期货市场已实现波动率的样本外预测精度最高。
第三步,运用估计的λ和ρ,可以得到模型(7)的半参数向前一步预测的表达式
(11)

1.4 估计方法的渐进性质
本文构建的股指期货市场波动率的半参数预测模型采用基于极值估计量的两阶段估计法进行估计,得到的参数估计值在一定的假设条件下是一致的,这些假设条件如下:
假设1 假设在模型(7)中,参数λ≠0,ρ>0,初始值RV1大于0;扰动项{Vt}是独立同分布且非负的连续随机变量;对于所有0 假设2 假设式(9)中的Λ是紧集,即Λ=[λmin,λmax],其中-∞<λmin<λ<λmax<0。 假设3 假设对于任意的λ′≠λ以及任意的i,有 E(RVt|RVt-1) 假设4 假设E(Vt)<∞ 值得注意的是,上述的假设条件都是基本的假设条件,并且容易检验。假设1能保证扰动项Vt是平稳和遍历的,从而可以推断已实现波动率序列RVt也是平稳和遍历的。假设2是标准的紧条件,假设3与非线性最小方差估计的识别条件密切相关,而假设4可以看成一个简单的矩条件。在假设1-假设4的条件下,本文得到如下命题: 假设6 存在r>2,满足下式 E|(RVt-E(RVt|RVt-1))· 值得注意的是,命题2中只给出了参数λ估计值的渐进分布。Barndorff-Nielsen等[21]的研究表明,非负AR(1)模型中的扰动项若具有指数分布,则模型参数的极值估计量为非对称和非标准的指数分布,而半参数模型(7)中参数ρ是采用基于极值估计量的两阶段估计法得到,其渐进分布的具体形式应更难获得,因此命题2中没有给出参数ρ的估计量渐进分布,但在下文中,采用Monte Carlo模拟来考察参数ρ和λ的估计值的渐近性质。 为了考察半参数预测模型(7)参数ρ和λ的估计值的渐近性质,本文设计了两个Monte Carlo模拟实验,采用由下式所示的非负模型产生实验数据 其中,本文采用独立同分布的标准指数分布生成扰动项ξt。参数λ和ρ采用1.3节阐述的基于极值估计量的两阶段估计法进行估计。 表1 模拟结果1 表2 模拟结果2 说明:参数λ和ρ的真实值分别为-0.42和0.68,模拟结果是通过5 000次的Monte Carlo模拟得到,样本大小均为T=1 200图和的柱状图 说明:参数λ和ρ的真实值分别为-0.28和0.54,模拟结果是通过5 000次的Monte Carlo模拟得到,样本大小均为T=1 200图和的柱状图 本文实证研究的数据样本为沪深300股指期货交易的5 min高频数据。沪深300股指期货于2010年4月16日正式交易,当月合约通常在每月第3个星期五(15日附近)进行交割。为了保证交易数据的完整性,本文选择2010年5月14日至2010年12月22日(总共146个交易日)沪深300股指期货当月连续合约的5 min高频交易数据作为研究样本。由于沪深300股指期货交易每天有4 h30 min交易时间,因此每个交易日可以记录54个5 min高频数据,全部样本合计7 884个5 min高频数据。本文数据来源于中国金融期货交易所 (http://www.cffex.com.cn)和Wind资讯金融终端8.2提供的高频行情数据终端(TAQEXP) 图3给出了沪深300股指期货的日对数收益率和已实现波动率序列图(由式(2)估计得到)。从图中可以看到,沪深300股指期货在2010年的4月-6月以及10月-12月波动幅度要大于7月-9月,并且对数收益率在大幅波动后往往会跟随一个大的波动,小幅波动后往往有更多的小幅波动,具有较为明显的波动聚集效应,表明沪深300股指期货收益变化的线性趋势不明显。 图3 日对数收益率序列和已实现波动率序列Fig.3 Daily logarithmic returns and realized volatilities 从表3的描述性统计结果可以看到,日收益率序列及其平方,已实现波动率序列都表现出明显的“尖峰厚尾”特征,这说明沪深300股指期货的波动幅度较为剧烈,远远超出了正态分布假定的范围(J-B统计量都很显著),只有对数已实现波动率序列和已实现波动率的幂(这里的幂取值为-0.139)非常接近于正态分布(J-B统计量在5%水平上不显著),但已实现波动率的幂比对数已实现波动率更加接近于正态分布,说明对已实现波动率进行幂转换导出正态分布比取对数更加有效,因此,本文构建的股指期货市场波动率的半参数预测模型采用已实现波动率的幂转换是合理的。此外,收益率序列之间不具有显著的自相关,而已实现波动率、收益率平方、对数已实现波动率以及已实现波动率的幂转换在很长的时间范围内都展现出非常显著的自相关特征(Q统计量都很显著),这从一方面说明了沪深300股指期货的波动率存在较为显著的长记忆性。进一步,ADF单位根检验和Pillips-Perron单位根检验结果显示各个序列都是平稳的。 表3 日收益率序列和已实现波动率序列的描述性统计 说明:**和***分别代表在5%和1%水平下显著,J-B为Jarque-Bera统计量,Q(n)为滞后n期的Ljung-Box Q统计量,ADF和P-P分别表示以最小AIC准则确定最优检验滞后阶数后得到的Augmented Dickey-Fuller单位根检验以及Pillips-Perron单位根检验结果。 文献中关于已实现波动率预测建模的研究最早开始于指数平滑模型(Exponential Smoothing,ES),其表述形式如下 (12) Andersen等[8]的研究发现,ARFIMA(p,d,q)模型能较好的捕获对数已实现波动率的长期记忆性,并且该模型对波动率的样本外预测效果要比GARCH(1,1)和RiskMetrics等一些基于收益平方的预测模型好。该模型(后文记为lnRV-ARFIMA)可以表述为 Φ(L)(1-L)d(lnRVt-μ)=Θ(L)εt (13) 最近,Corsi[9]基于异质市场假说的思想和HARCH模型构建了一个简单的已实现波动率近似长记忆模型——异质性自回归已实现波动率模型(Heterogeneous Autoregressive Realized Volatility model),后面记为HAR模型。该模型可表述为 (14) 由于本文新构建的半参数预测模型仅考虑扰动项的分布形式、已实现波动率序列的相关关系以及异方差,而并没有考虑已实现波动率的其他特征,如不对称性等,因此在本文的实证研究中只评价和比较新构建的半参数预测模型与4种不考虑波动率其他特征的ARFIMA模型(ARFIMA(1,d,0)、ARFIMA(0,d,1)、ARFIMA(1,d,1))和HAR模型的滚动时间窗的样本外预测精度,旨在研究通过幂转换以及不设定扰动项的具体相关结构和分布形式构建的半参数模型与经典模型相比确实进一步提高了波动率的预测精度。同时,本文实证研究还评价和比较半参数预测模型与RV-LinAR模型(式(5))和lnRV-LinAR模型(式(6))的滚动时间窗的样本外预测精度,旨在研究幂转换以及不设定扰动项的具体相关结构和分布形式确实进一步改善的RV-LinAR模型和lnRV-LinAR模型对已实现波动率的预测能力。本文的滚动时间窗的样本外预测方法如下: 图4 已实现波动率半参数模型在预测样本区间的预测结果Fig.4 Forecasting results for semiparametric model during forecasting sample (15) 本文选取当b=1,-1,2,-2,3,-3时的6类稳健损失函数来评价和比较半参数预测模型、ARFIMA(1,d,0)模型、ARFIMA(0,d,1)模型、ARFIMA(1,d,1)模型、HAR模型、ES模型、RV-LinAR模型以及lnRV-LinAR模型的样本外预测精度。 在波动率预测评价和比较中还存在一个特别值得关注的问题,即在某一特定的数据或者某一种损失函数下,得到的预测模型预测能力优劣的结论,可能无法推广到其他的损失函数或者其他类似的数据样本中。Hansen等[23]基于Bootstrap提出的SPA检验法(Test for Superior Predictive Ability),较好地解决这一问题,但SPA检验需要选择基础模型。为了克服这个缺陷,本文采用SPA检验的修正形式——MCS检验(参见文献[25])来评价和比较各类股指期货市场波动率预测模型的预测精度。 dij,m=Lb,i,m-Lb,j,m (16) MCS检验的过程是从候选模型M0中序贯的剔除一些预测能力较差的模型。因此,在每一步中,零假设条件是任意两个候选模型具有相同的预测能力(Equal Predictive Ability, EPA),可以表述如下: (17) (18) 表4给出了10 000次Bootstap模拟得到的MCS检验结果,表中第一列表示当b=1,-1,2,-2,3,-3时的6类稳健损失函数(见式(15)),表中数字表示MCS检验的p值,p值越大,表明越拒绝零假设。小写字母m加下标表示不同的波动率预测模型。其中,m1表示ES模型,m2表示RV-LinAR模型,m3表示lnRV-LinAR模型,m4表示ARFIMA(1,d,0)模型,m5表示ARFIMA(0,d,1)模型,m6表示ARFIMA(1,d,1)模型,m7表示HAR模型,m8表示半参数模型。按照Hansen等[25]的建议,本文设定p=0.1为基准p值,p值小于0.1的波动率预测模型是样本外预测能力差的模型,将在MCS检验过程中被剔除,而p值大于0.1的波动率预测模型是样本外预测能力较好的模型,在MCS检验中能幸存下来。 从表4可以看出,当稳健损失函数取b=1,b=-1,b=3时,ES模型 、RV-LinAR模型、lnRV-LinAR模型、ARFIMA(1,d,0)模型、ARFIMA(0,d,1)模型、ARFIMA(1,d,1)模型以及HAR模型不管是基于TR统计量还是TSQ统计量得到的MCS检验的p值都小于0.1,意味着这7类波动率预测模型将在MCS检验过程中被剔除,唯一幸存下来的模型是半参数预测模型,因此,在稳健损失函数取b=1,b=-1,b=3时,相对于其他7类预测模型,半参数预测模型是样本外预测能力最好的模型。当稳健损失函数取b=-2,b=-3时,ES模型 、RV-LinAR模型、lnRV-LinAR模型、ARFIMA(1,d,0)模型、ARFIMA(0,d,1)模型、ARFIMA(1,d,1)模型的MCS检验p值不管是基于TR统计量还是TSQ统计量都小于0.1,在MCS检验过程中将被剔除,HAR模型和半参数预测模型的MCS检验p值都大于0.1,两者在MCS检验中最终都能幸存下来,但在p=0.1的基准p值下,无法判断HAR模型和半参数预测模型孰好孰坏,因此,在稳健损失函数取b=-2,b=-3时,相对于其他6类预测模型,HAR模型和半参数预测模型是样本外预测能力最好的模型,两者对股指期货市场波动率的预测能力相当。然而,当稳健损失函数取b=2时,只有ES模型的MCS检验p值小于0.1,其他预测模型的p值都大于0.1,因此,当稳健损失函数取b=2时,除ES模型外,其他预测模型都能幸存下来,它们的预测能力相当,这也说明稳健损失函数取b=2时,对波动率预测精度不敏感,在MCS检验中无法区分各预测模型预测能力的好坏。 总而言之,本文新构建的股指期货市场波动率的半参数预测模型,在绝大多数的稳健损失函数下,相对于其他模型来说,是预测精度最高的模型。 表4 不同已实现波动率模型的MCS检验结果 本文在线性非负模型的基础上,通过对高频环境下股指期货市场的已实现波动率进行幂转换,同时不设定模型非负扰动部分的相关结构以及具体分布形式,构建了一个股指期货市场波动率的半参数预测模型,用来预测股指期货市场的波动率。该模型同时克服了经典的Box-Cox模型的“截取问题”和ARFIMA模型需要设定扰动项具体结构以及不能存在异方差的缺陷。模型采用基于极值估计量的两阶段估计法进行估计,通过Monte Carlo模拟实验发现该估计方法的渐进性质表现良好。最后,以沪深300股指期货的5 min高频数据为例,运用滚动时间窗的样本外预测和最新发展起来的具有Bootstrap特性的MCS检验,在多种稳健损失函数下,实证评价和比较了新构建的半参数预测模型与指数平滑模型(ES模型)、线性高斯模型、对数-线性高斯模型以及HAR模型对高频环境下沪深300股指期货波动率的预测能力。实证结果表明:在多种稳健损失函数的评价标准下,本文构建的股指期货波动率的半参数预测模型是预测预测能力最好的模型。 这项研究具有多重现实意义:首先,有利于股指期货投资者预先作出合理的投资决策。合理预测股指期货市场波动率能使投资者更早地认识到股指期货市场未来价格波动率的变动规律,在特定的投资目标下作出更为合理的投资决策;其次,有利于提高机构和个人投资者的风险管理水平。股指期货是一柄“双刃剑”,在为资本市场提供风险管理工具的同时亦难以摆脱衍生产品固有的高风险特性。其价格的急剧性波动往往是机构投资者破产的最大原因,因此准确地预测股指期货市场波动率将有利于投资者合理控制投资风险;最后,有利于监管部门制定相关政策以及提高监管水平。 参考文献: [1] ENGLE R F. Autoregressive conditional heteroskedasticity with estimates of the variance for U.K. infortion [J]. Econometrica, 1982, 50(3):987-1007. [2] BOLLERSLEV T. Generalized autoregressive conditional heteroskedasticity [J]. Journal of Econometrics, 1986, 31(2): 307-327. [3] TAYLOR S J. Modelling stochastic volatility[J]. Mathematica Finance, 1994, 4(2):183-204. [4] ANDERSEN T G, BOLLERSLEV T. Answering the critics:yes, ARCH models do provide good volatility forecasts [C]//National Bureau of Economic Research, 1997:1-37. [5] ANDERSEN T G, BOLLERSLEV T, DIEBOL F X, et al. Exchange rate returns standardized by realized volatility are (nearly) Gaussian [J]. Multinational Finance Journal, 2000, 4(3):159-179. [6] ANDERSEN T G, BOLLERSLEV T, DIEBOL F X, et al. The Distribution of realized exchange rate volatility [J]. Journal of the American Statistical Association, 2001, 96(3):42-55. [7] ANDERSEN T G, BOLLERSLEV T, DIEBOL F X, et al. The Distribution of realized stock return volatility [J]. Journal of Financial Economics, 2001, 61(5):43-76. [8] ANDERSEN T G, BOLLERSLEV T, DIEBOL F X, et al. Modelling and forecasting realized volatility [J]. Econometrica, 2003, 71(2):579-625. [9] CORSI F. A simple approximate long memory model of realized volatility [J]. Journal of Financial Econometrics, 2009, 7:174-196 [10] 郭名媛,张世英. 赋权已实现波动及其长记忆、最优抽样频率选择[J]. 系统工程学报,2006, 21(6):568-573. [11] 魏宇,余怒涛. 中国股票市场的波动率预测模型及其SPA检验[J]. 金融研究,2007, 7:138-150. [12] 魏宇. 金融市场的多分形波动率测度、模型及其SPA检验[J]. 管理科学学报,2009, 12(5):88-99. [13] AREAL N M, TAYLOR S J. The realized volatility of FTSE-100 futures prices [J]. Journal of Futures Markets, 2002, 22(7):627-648. [14] XIE H, LI J. Intraday volatility analysis on S&P 500 stock index future [J]. International Journal of Economics and Finance, 2010, 2(2):26-34. [15] 魏宇. 沪深300股指期货的波动率预测模型研究[J]. 管理科学学报,2010, 13(2):66-76. [16] BARNDORFF-NIELSEN O E, SHEPHARD N. Non Gaussian Ornstein-uhlenbeck-based models and some of their uses in financial economics [J]. Journal of the Royal Statistical Society:Series B,2001, 63(2):167-241. [17] BARNDORFF-NIELSEN O E, SHEPHARD N. Econometric analysis of realized volatility and its use in estimating stochastic volatility models [J]. Journal of the Royal Statistical Society, Series B, 2002, 64(2):253-280. [18] YU J, YANG Z. A class of nonlinear stochastic volatility models[C]//Singapore Management University, 2006:1-24. [19] ANDERSEN T G, BOLLERSLEV T. Answering the skeptics:Yes, standard volatility models do provide accurate forecasts [J]. International Economic Review, 1998, 39(4):885-905. [20] MARTENS M. Measuring and forecasting S&P 500 index‐futures volatility using high‐frequency data [J]. Journal of Futures Markets, 2002, 22(6):497-518. [21] BARNDORFF-NIELSEN O E, SHEPHARD N. Likelihood analysis of a first-order autoregressive model with exponential innovations [J]. Journal of Time Series Analysis, 2003, 24(3):337-344. [22] PHILLIPS P C B. Time series regression with a unit root [J]. Econometrica, 1987, 55(2):277-301. [23] HANSEN P R, LUNDE A. A test for superior predictive ability [J]. Journal of Business and Economic Statistics, 2005, 23(4):365-380. [24] POTTON A J. Volatility forecast comparison using imperfect volatility proxies [J]. Journal of Econometrics, 2011, 160(1):246-256. [25] HANSEN P R, LUNDE A, JAMES M N. The model confidence set [J]. Econometrica, 2011, 79(2):453-497.




2 Monte Carlo模拟实验及结果




3 实证分析
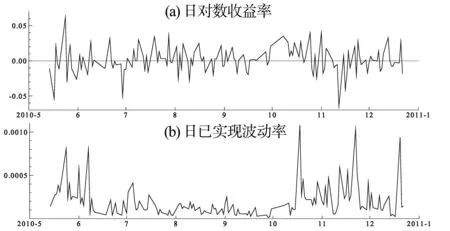
3.1 数据以及描述性分析

3.2 其他已实现波动率预测模型



3.3 滚动时间窗的样本外预测方法
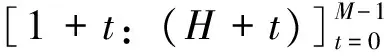

3.4 基于Bootstrap模拟的MCS检验


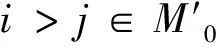

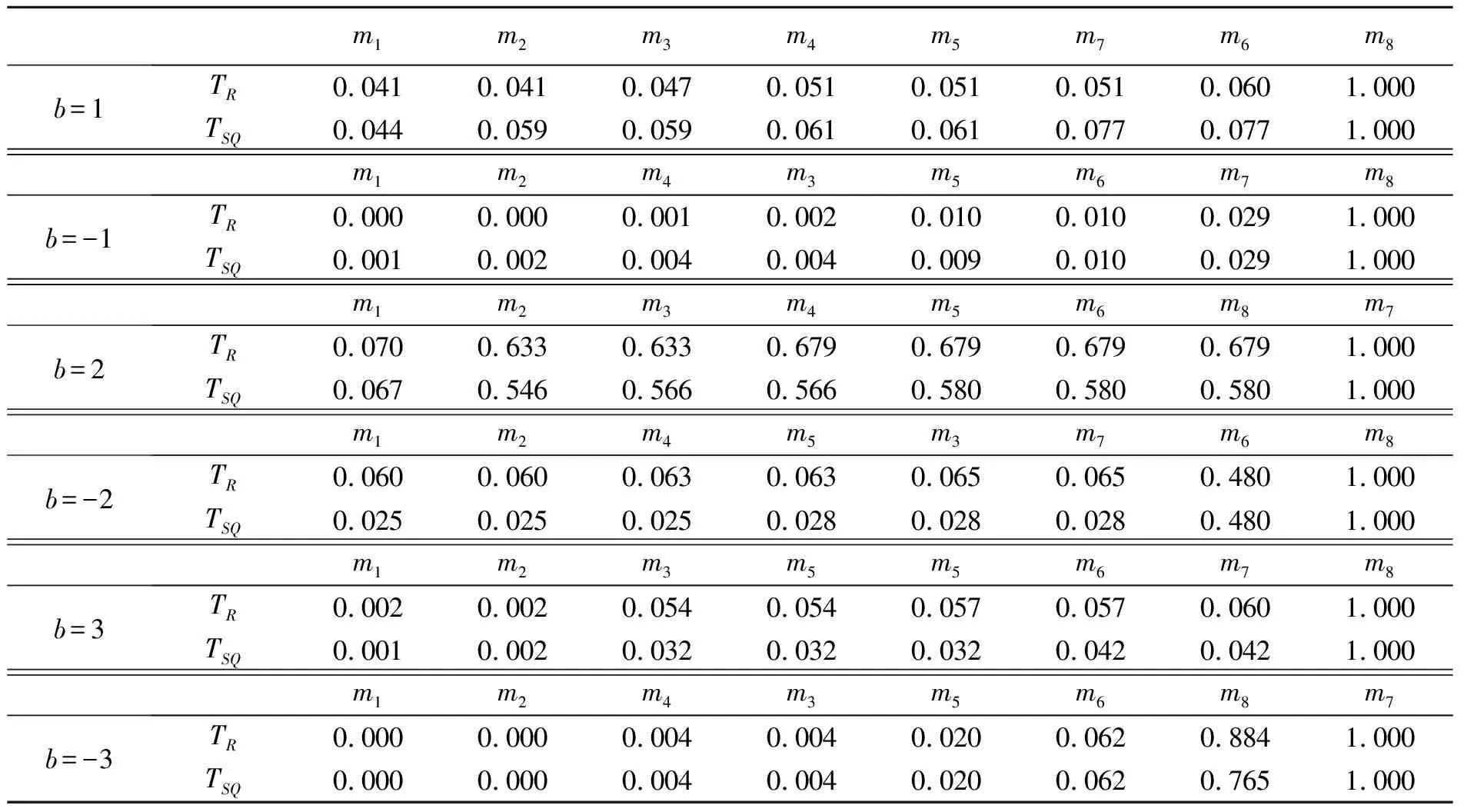
3.5 MCS检验评价比较结果
4 结 论
