时间测度链上一类三阶动力方程的振动准则

张晓建，杨甲山

(邵阳学院理学与信息科学系，湖南 邵阳 422004)

近年来时间测度链上动力方程有关理论的研究引起了国内外学术界的广泛兴趣和高度关注[1-13]。本文考虑下面的时间测度链上一类非常广泛的具有非线性中立项的三阶非线性变时滞动力方程

{r(t)φ([a(t)yΔ(t)]Δ)}Δ+

P(t)F(φ(x(δ(t))))=0,t∈T,t≥t0

(1)

这里y(t)=x(t)+B(t)g(x(τ(t))),T为任意时间测度链;φ(u)=|u|λ-1u,λ≥1为实常数;r(t),a(t),B(t),P(t) ∈Crd(T,R);τ(t),δ(t)均为定义在T到T上的滞量函数;g(u),F(u)∈C(R,R),且ug(u)>0(u≠0),uF(u)>0(u≠0)。

关于时间测度链上的分析理论和时间测度链上动力方程的基本理论可参阅文献[1]。在本文中，讨论的是方程解的振动性, 所以总假设时间测度链T是无界的:supT=+∞。设t0∈T且t0>0, 定义时间测度链区间[t0,+∞)T=[t0,+∞)∩T。方程(1)的解是指定义在T上满足方程(1)的非平凡实值函数x(t),t∈T。方程(1)的解x(t)称为振动的, 如果x(t)既不最终为正, 也不最终为负。否则, 称为非振动的。方程(1)称为振动的, 如果它的所有解都是振动的。本文仅关注方程(1)的不最终恒为零的解, 并总假设下列条件成立：

(H2) 0≤B(t)≤1;P(t)>0;r(t)>0,rΔ(t)≥0;a(t)>0,aΔ(t)≥0。

关于方程(1)的特殊情形,已有文献作过研究[2-6], 本文的目的是研究方程(1)的振动性, 改善对方程的条件限制, 得到了该方程振动的几个新的充分条件, 推广并改进了现有文献中的某些结果。

1 几个基本引理

引理1[1]若x(t)是Δ可微的且最终为正或最终为负，则

(2)

引理2[7]设下面的条件成立：

引理3 设x(t)是方程(1)的一个最终正解, 则∃t1∈[t0,+∞)T, 当t∈[t1,+∞)T时, 只有下列两种情况：

(i)y(t)>0,yΔ(t)>0,[a(t)yΔ(t)]Δ>0,{r(t)φ([a(t)yΔ(t)]Δ)}Δ<0;

(ii)y(t)>0,yΔ(t)<0,[a(t)yΔ(t)]Δ>0,{r(t)φ([a(t)yΔ(t)]Δ)}Δ<0。

证明完全类似于[4]中的引理2.1, 在此从略。

引理4[8]设a,b为非负实数, 则rabr-1-ar≤(r-1)br,r>1,等号成立当且仅当a=b。

引理6 设x(t)是方程(1)的满足引理3情形(ii)的一个正解, 如果

(3)

或者

(3)'

{r(t)φ([a(t)yΔ(t)]Δ)}Δ=

-P(t)F(φ(x(δ(t))))≤

-LP(t)(x(δ(t)))λ<0

(4)

所以

{r(t)φ([a(t)yΔ(t)]Δ)}Δ≤

(5)

若(3)成立，则对(5)式两边从t2到t(t∈[t2,+∞)T)积分,得

r(t)φ([a(t)yΔ(t)]Δ)≤

r(t2)φ([a(t2)yΔ(t2)]Δ)-

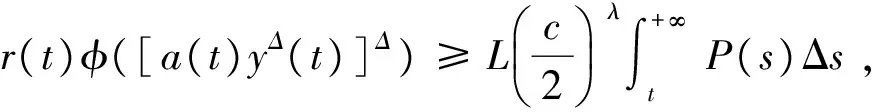
上式两边从t2到t(t∈[t2,+∞)T)积分, 得

y(t)≤y(t2)-

Δv→-∞(t→+∞)

鉴于此, 以下均假设(3)或(3)'之一是成立的。

2 主要结果和证明

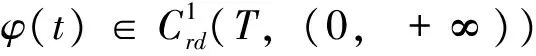
(6)

[1-βB(t)]y(t)≤x(t)

(7)

定义广义的Riccati变换

(8)

则V(t)>0(t∈[t1,+∞)T), 注意到(4), (8)式, 进一步可得

(9)

令u(t)=a(t)yΔ(t), 则由引理3的(i), 得u(t)>0,uΔ(t)>0, 由

{r(t)[a(t)yΔ(t)]Δ}Δ={r(t)uΔ(t)}Δ=

rΔ(t)uΔ(σ(t))+r(t)uΔΔ(t)<0

a(σ(t))yΔ(σ(t))≤

(10)

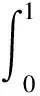
[(a(t)yΔ(t))λ]Δ≥

λ(a(t)yΔ(t))λ-1(a(t)yΔ(t))Δ

(11)

将(7), (10),(11)式代入(9)式, 得

(12)

(13)

因此, 由(10) ,(13)式, ∃T0∈[t0,+∞)T且T0≥max{t2,t1/2}, 使得当t∈[T0,+∞)T时, 有

在台达吴江生产制造基地，生产台达自动化产品的智能制造示范线已落成投运，通过引入工业机器人、RFID检测识别、机器视觉及AGV物料配送等智能化设备，配合制造执行系统（MES），实现产线优化与升级。生产使用面积减少62%、产线操作人员数降低88%的同时，产能提升40%。实践的成功经验将在台达各厂区上百条产线复制展开，结合大数据与AI分析技术持续优化完善，最终成为工业客户实施“智造升级”时至关重要的保障。

将上式代入(12)式, 得

(14)

现取

代入引理4中的不等式, 得

将其代入(14)式, 得

φ(σ(t))Ψ(t)≤-VΔ(t)+

(15)

两边积分, 得

所以

上式取上极限, 得与(6)式矛盾! 定理证毕。

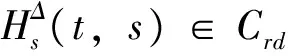
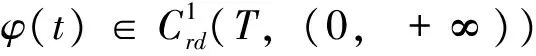
(16)

证明同定理1, 只需证明x(t)满足引理3中的情形(i)即可。由定理1的证明可得(15)式, 即当s∈[T0,+∞)T时, 有

上式两边同时乘以H(t,s), 并从T0到t(t∈[T0,+∞)T)积分, 由时间测度链上的分部积分法可得

H(t,T0)V(T0)≤H(t,t0)V(T0)

于是

上式取上极限, 得与(16)式矛盾! 定理证毕。

注2 选择恰当的不同的函数H(t,s)和φ(t), 就能得到方程(1)的许多不同的具体振动准则。 现在定理2中取H(t,s)=(t-s)m,φ(t)=M(M>0为常数), 则得

推论2 如果存在常数m≥1使得

此推论就是三阶微分方程的Kamenev型振动准则的推广。

例1 考虑三阶微分方程

{t3[(tx'(t))']4}'+t2(t-1)3·

(4t2-11t+3)x4(t)=0,t≥2

例2 考虑时间测度链上的三阶动力方程

P(t)F(φ(x(δ(t))))=0,t∈2Z,t≥2

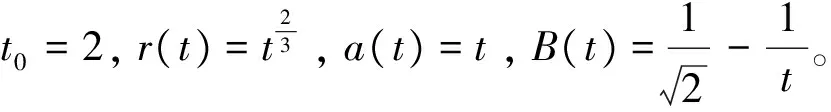
参考文献：

[1] BOHNER M, PETERSON A. Dynamic equations on time scales, an introduction with applications[M]. Boston: Birkhauser, 2001.

[2] HAN Z, LI T, SUN S, et al. Oscillation criteria for third order nonlinear delay dynamic equations on time scales[J]. Ann Polon Math, 2010, 99: 143-156.

[3] HAN Z, LI T, SUN S, et al. Oscillation behavior of third-order neutral Emden-Fowler delay dynamic equations on time scales[J]. Adv Diff Eq, 2010: 1-23.

[4] HASSAN T S. Oscillation of third order nonlinear delay dynamic equations on time scales[J]. Math Comput Model, 2009, 49:1573-1586.

[5] ERBE L, HASSAN T S, PETERSON A. Oscillation of third order nonlinear functional dynamic equations on time scales[J]. Differential Equations Dynamical Systems, 2010,18:199-227.

[6] 张少艳，王其如. 一类三阶非线性时标动态方程的振动性[J]. 中山大学学报：自然科学版, 2012, 51(4): 50-55.

[7] SAHINER Y. Oscillation of second order delay differential equations on time scales[J]. Nonlinear Analysis, TMA, 2005, 63: e1073-e1080.

[8] AGARWAL R P, BOHNER M, LI W T. Nonoscillation and oscillation: Theory for functional differential equations[M].New York: Marcel Dekker, 2004.

[9] ERBE L, PETERSON A, SAKER S H. Hille and Nehari type criteria for third order dynamic equations[J]. J Math Anal Appl, 2007, 329: 112-131.

[10] 李同兴，韩振来，张承慧，等. 时间尺度上三阶Emden-Fowler动力方程的振动准则[J]. 数学物理学报, 2012, 32A(1): 222-232.

[11] 张全信，高丽，刘守华. 时间尺度上具阻尼项的二阶半线性时滞动力方程的振动准则(Ⅱ)[J].中国科学：数学，2011, 41(10): 885-896.

[12] 韩振来，孙书荣，张承慧. 时间尺度上二阶中立型时滞动力方程的振动性[J]. 中山大学学报：自然科学版,2010,49(5):21-24.

[13] 杨甲山. 时间测度链上一类具阻尼项的二阶动力方程的振动准则[J]. 上海交通大学学报, 2012, 46(9):1529-1533，1538.