高海拔地区控制网长度变形异常的处理

　

(中铁工程设计咨询集团有限公司济南设计院， 山东济南　250022)

1　概况

胜利西三煤矿销煤铁路专用线位于内蒙古自治区锡林郭勒盟境内，线路自锡林浩特站北咽喉引出，至胜利西三煤矿装车站，正线全长5.228 km，预测运量为370×104t/年，设1个装车站。

2　投影长度变形的构成

我国坐标系统是采用高斯-克吕格正形投影(简称“高斯投影”)，即先由大地面投影到参考椭球面，再由参考椭球面投影到高斯平面；而高程面则是投影到大地水准面上。变形主要由以下两个方面构成。

(1)高程改正

控制点的坐标是在参考椭球面上平差计算而得，全站仪或电磁波测距仪所测的距离，应将其归算到参考椭球面上，才能进行平差计算。

则改化公式为

式中D为大地点Q1和Q2之间的斜距，H1和H2分别为Q1和Q2的大地高，RA为地球曲率半径。

如果在海拔高度较低的地区，这项改正很小，但在海拔较高的高原和山地，就不得不考虑其影响。

(2)高斯投影改正

高斯投影是正形投影，保证了投影角度的不变性，图形的相似性以及在某点各方向上的长度比的同一性。我国采用的地图投影即为高斯投影，规定按经差6°和3°进行投影分带，在大比例尺测图和工程测量中采用3°带投影，工程控制网也可采用任意带投影。

高斯投影将椭球面上的边长归算到平面上，将不可避免地产生长度变形，这种变形在中央子午线上为0，离中央子午线越远所产生的变形越大。高斯投影改正的计算公式为

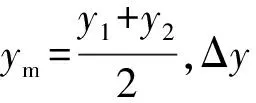
在平均海拔高程很大或远离中央子午线的地区，长度变形的影响很大。对于导线测量，可导致坐标闭合差和边长相对闭合差的超限。而对于一些工程测量，如公路、桥梁、隧道的施工放样，不考虑其影响，将导致整个工程精度的低下。

3　减小投影长度变形的常用方法

选择合适的参考椭球投影面，抵偿高斯分带投影变形。

平移高斯投影的中央子午线，抵偿观测边长归算至参考椭球面的变形影响。

综合采用以上两种方法，共同抵偿观测边长归算至参考椭球面和高斯投影的变形影响。

4　工程应用实例

本工程所在区域有煤矿提供D级控制点两个，为满足本工程的设计要求，现场又重新增设了E级控制点四个，但在接下来的工作中发现，GPS测出两点之间的距离与全站仪测出两点之间的距离有较大差别。两个D级GPS控制点如表1，GPS测得两点之间的距离与全站仪测得两点之间的距离如表2。

《铁路工程测量规范》规定：边长投影变形值宜不大于25 mm/km，以满足勘测设计和施工测量的要求，这一要求也是我国各行业建立工程测量控制网所采取的基本原则。

D级控制点的坐标为：北京54坐标系统，6°带，中央子午线117°，高程为85高程系统，高程投影面为0，而作业范围所在区域中央子午线为116°，高程在1 000 m左右。

表1　GPS控制点坐标　m

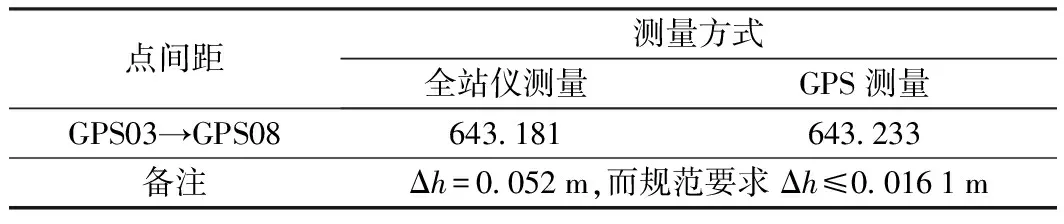
表2　两点之间的距离对比　m

由此可以看出，在平均海拔高程很大或远离中央子午线的地区，长度变形较大，对工程的精度影响也最大。为此从这两个方面入手制定如下对策：加密控制网，并利用已知点的成果(中央子午线117°，0高程投影面)为约束条件获得加密控制点坐标，将新控制网的成果换算为中央子午线116°，1 000高程投影面的成果。

坐标变换的基本情况如表3所示。

加密控制点网形如图1所示。

图1　加患控制点网形

外业静态测量完成后，内业经过了标准化整理、基线处理、控制网平差几个过程，主要技术指标如基线向量异步环闭合差、重复基线较差、三维平差二维平差后方位角精度及边长精度等均能达到相应的规范要求。三维无约束平差计算后精度统计如表4所示。

由三维无约束平差精度统计表可以看出：控制网的基线向量网自身的内符合精度较高，基线向量网没有明显的系统误差和粗差，基线向量网的质量比较可靠，可以进行下一步的二维约束平差。

二维约束平差计算后精度统计如表5所示。

二维约束平差后，基线最弱边精度为1/2 182 000，方向中误差最大为0.09″，基线向量精度满足《铁路工程测量规范》(TB10101—2009)中五等最弱边相对中误差≤1/40 000、方向中误差≤3.0″的精度要求。

重新复测GPS03、GPS08之间的距离如表6所示。

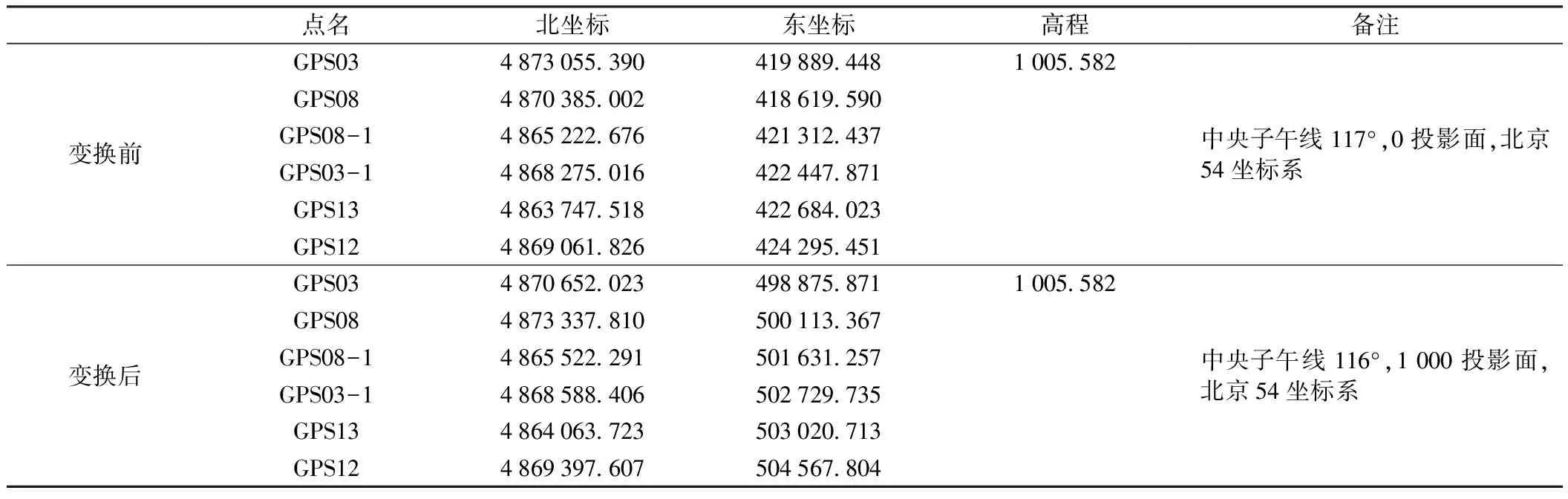
表3　GPS控制点坐标变换　m

表4　三维无约束平差精度统计

表5　二维约束平差精度统计

表6　两点之间的距离对比　m

5　结束语

经过理论分析及数据处理，证明采用平移投影中央子午线结合抬高投影面处理长度变形超限方法的正确性，满足了本次测量工作的精度要求。处理投影长度变形的方法多种多样，应根据工程的实际情况采用最适宜的解决方法。

[1]徐正扬，等.大地控制测量学[M].北京：解放军出版社，1992

[2]陈永奇.工程测量学[M].北京：测绘出版社，1995

[3]郝瀛.铁道工程[M].北京：中国铁道出版社，2000

[4]冯仲科.测量学原理[M].北京：中国林业出版社，2002

[5]魏二虎,黄劲松.GPS测量操作与数据处理[M].武汉：武汉大学出版社，2004

[6]中铁一院.铁路工程卫星定位测量规范[S].北京：中国铁道出版社，2010

[7]中铁二院.铁路工程测量规范[S].北京：中国铁道出版社，2009

[8]张竞强，李汝晓.减少测区的长度变形[J].现代测绘，2005(3)