利用向量代数和空间解析几何原理确定岩层产状的方法

2013-04-16

铁道勘察 2013年2期

(铁道第三勘察设计院集团有限公司，天津　300251)

山区铁路勘察时，岩层产状的量测非常重要，特别是路堑工程，产状的准确性直接关系到开挖边坡是否顺层的判定。但是，有时工程附近没有很好的岩层出露，不能就近使用罗盘直接测量，只能借鉴附近区域的数据。另外，野外出露的岩层面受风化作用的影响，并不平整，不便找代表性的平面测量。当遇到软质岩或岩层倾角平缓时，又会受到张开风化裂隙的影响，测量误差有时较大，而且多组数据的离散性也较大，给勘察设计带来了困难。这就需要探索能够确定岩层产状的更为准确、有效的方法。

1　几种常见的求解岩层产状的方法

实践中，采用间接法计算岩层产状的方法较多，常见的主要有以下几种。

1.1　三点法[1]

原理：已知同一倾斜岩层面上不在同一直线上的三点的空间坐标，过最高点与最低点的连线上可以找到与中间点高程相等的点，该点与中间点连线即为岩层的走向线，过最高点或最低点做一走向线，并做两走向线的公垂线，则可根据立体几何解析原理求解出倾向和倾角。

该方法精度高，但是计算步骤较多。

1.2　相邻等高线法[1]

在地形地质图上找到岩层界线与同一等高线的两个交点，交点连线即为走向线，过该岩层界线与第二条等高线的交点做走向线，过任意点做两条走向线的公垂线，以任一垂足为端点，在走向线上按比例截取与两条走向线高程差相等的线段，得直角三角形，高程差线段边的对角即为岩层倾角，平面上使用量角器测量。其原理与三点法是一样的。

该方法需要详细的地质调绘资料，精度低；岩石出露条件不好时，应用受到限制。

1.3　视倾角公式反算法[2，3]

原理：已知同一倾斜岩层面上不在同一直线上的三点的空间坐标，任意两点连线视为剖线，则剖线走向可求，视倾角亦可根据点坐标求解，取任意两条剖线，根据视倾角换算公式列两个方程，计算出岩层倾向和倾角。

该方法精度高，但是计算公式繁琐，需要分别修正视倾向和真倾向值，计算步骤较多。

1.4　单个倾斜钻孔计算法[4，5]

其原理是根据钻孔的测斜数据和岩芯轴法角与岩层法线之间的关系，建立三元线性方程，求解岩层产状。

该法在煤炭领域应用较广，由于需要测井数据，一般工程勘察中不适用，仅长大隧道工程有测井资料时可以借鉴。

三点法、相邻等高线法和视倾角公式反算法均利用了不在同一直线上的三点确定一个平面的几何原理。笔者通过摸索，利用向量代数和空间解析几何的基本原理，总结了两种求解岩层倾向和倾角的方法。

2　空间解析几何法

已知不在同一直线上三点的空间坐标，则可利用向量代数的原理求得该岩层面的平面方程，该平面与水平面的交线即为岩层的走向线。利用空间解析几何的原理，求解水平面内走向线的垂线方程，可得岩层倾向线方程，求出倾向线方程与大地坐标系X轴的夹角，判断倾向所在象限，对夹角进行修正即可求得岩层的倾向。岩层面的平面方程与水平面的夹角即为岩层的倾角。其原理与岩层走向、倾向、倾角的基本概念吻合。

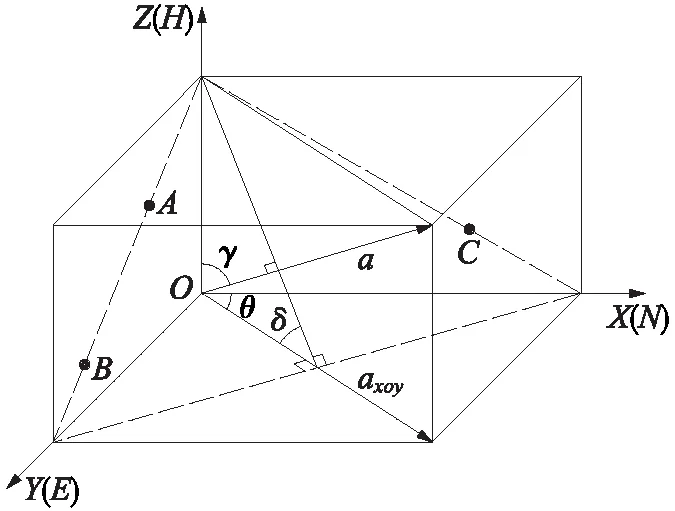
图1　岩层产状计算示意

2.1　利用向量代数的原理求解岩层面的平面方程

如图1所示，设不在同一直线上的任意三点坐标分别为

A(XA，YA，HA)
B(XB，YB，HB)
C(XC，YC，HC)

其中X和Y分别为大地坐标系内点的北坐标和东坐标，H为点的高程。

利用向量代数的原理可得

(1)

式中

(2)

于是，过A、B、C三点的平面方程，即岩层平面方程可表示为

axx+ayy+azz+D=0

(3)

2.2　求岩层走向线方程

过坐标原点的水平面方程为

z=0

(4)

与岩层面的平面方程联立，即为两平面的交线方程，亦即岩层走向线方程：

(5)

式(5)中两方程简化可得

axx+ayy+D=0

(6)

2.3　求岩层倾向

倾向线方程与走向线方程相互垂直，两直线的斜率乘积应为-1，则由式(6)可得倾向线方程为

ayx-axy+M=0

(7)

则倾向线与X轴的夹角θ′可由下式求得

(8)

夹角θ′根据ax和ay值的正负进行修正即可得岩层倾向θ，如表1。

表1　倾向基本角θ′修正

2.4　求岩层倾角

岩层的倾角δ，即岩层面与水平面的夹角，可由式(3)、(4)求得

(9)

3　向量代数法

过不在同一直线上三点确定的平面法向量的z轴方位角为γ，其取值范围为0°～360°，当不考虑γ′的方向性，约束其取值范围为0°～90°时，由图1可以证明：法向量与z轴的夹角γ′与岩层的倾角δ相等。

法向量在xoy平面的投影向量的方向即为岩层倾向。

求解过程如下：

(1)求解岩层面法向量，与式(1)相同，记为a(ax，ay，az)；

(2)设a(ax，ay，az)在z轴方向的方位角为γ，则

(10)

约束γ的取值范围为0°～90°，则

(11)

可见，式(11)与式(9)完全一致，也就是说γ′与岩层的倾角δ相等。

(3)岩层面法向量a(ax，ay，az)在水平面上的投影向量为axoy(ax，ay，0)，设沿X轴正方向的任一向量b(bx，0，0)，则axoy(ax，ay，0)与b(bx，0，0)夹角可由下式求得

(12)

由式(12)可求得

(13)

式(13)与式(8)其实是相同的。

4　获得点坐标的方法

工程勘察中，点坐标的获取方法主要有以下两种。

(1)使用测量仪器实测

野外寻找代表性的地质剖面，找到层位稳定(岩层连续、厚度变化小)，具代表性的标志层，使用仪器实测，实测标志层层面至少三个点的坐标，即可计算出岩层产状。为减小误差，可增加采取点的数量或选取不同的标志层，任意组合三个点的坐标分别计算产状，统计求平均值。

优点是方便、快捷，可以短时间内采集大量数据求平均值，精确度高。但需注意采集点的间距不宜太小，太小可能出现较大误差。坐标值应精确至cm级计算。目前铁路、公路勘测已经广泛使用RTK技术作业，此方法精度高，受场地条件影响小。

(2)利用钻孔资料计算

利用三个不共线的钻孔地层资料，找到相同的层位，计算层位顶面高程，即可计算求得产状。

工程附近缺少良好的地质剖面时，使用此方法较为合适，可求解某特定层位的产状。缺点是不能直观判断各岩层的稳定性，岩性接近时，有时不好选择标志层，而且当标志层厚度变化较大时，计算结果代表性不强。为找到合适的标志层，减小误差，有时需要增加钻孔深度，选择多个标志层。对钻探质量要求较高，孔深误差需得到严格控制，岩芯摆放次序不能乱、深度需准确。另外，钻孔间距和钻孔间夹角均不宜太大或太小。