基于EGM2008模型的GPS高程拟合方法在铁路勘测中的应用研究

　

(中铁第四勘察设计院集团有限公司，湖北武汉　430070)

铁路勘测过程中，线路沿线的高程数据是确定线路纵断面的基础数据。这些高程数据要么是采用几何水准测量方法测量的正常高，要么是采用GPS高程拟合方式拟合出的正常高。传统的几何水准测量虽然精度相对较高，但作业效率低，尤其在相对高差大的山区及荒漠无人区，不能很好地满足大量高程数据快速采集的要求。近年来，GPS技术以其高精度、全天候、低成本、高效率的优点被广泛应用于铁路勘测的各个环节。GPS测量的参考椭球为WGS84椭球，GPS直接测得的高程是相对于WGS84椭球面的大地高，与勘测过程中采用的正常高系统不一致，故将GPS测得的大地高用GPS高程拟合的方法转换为工程中需要的正常高是一项必要工作。常规的GPS高程拟合方式需要联测较为密集的高程点，且拟合精度较低。

1　EGM2008地球重力场模型

地球重力场模型是采用一类基本参数的集合，用逼近或拟合的方式来描述和表示地球重力场的模型。2008年4月，NGA(美国国家地理空间情报局National Geospatial-Intelligence Agency)发布了最新的全球重力场模型，命名为EGM2008[1]。EGM2008研究和总结了以往地球重力场模型理论和经验，采用了各种先进的基础数据，其中包括：

①以PGM2007为基础演变出来的PGM2007B为参考模型；

②利用了带有ITG-GRACE03S位系数信息以及相应协方差信息的GRACE卫星卫星跟踪数据；

③利用了卫星测高数据(TOPEX)和全球5′×5′空间分辨率的地面重力异常数据；

④利用了高精度、广域覆盖的地面重力数据。

EGM2008重力场模型的球谐系数阶次完全至2 159阶，扩展到2 190阶，相当于约9 km的模型空间分辨率，是目前最高分辨率和精度的重力场模型。EGM2008重力场模型提供了包括2 190阶次的全球重力场模型、全球5′×5′网格重力异常、全球5′×5′、2.5′×2.5′网格大地水准面、全球5′×5′网格垂线偏差(ξ，η)的最终成果。

针对我国情况，国内学者进行了深入的研究：EGM2008重力场模型提供的高程异常在我国大陆地区的总体精度为20 cm，中东部地区12 cm，北方地区达到9 cm，西部地区为24 cm[2]。应用EGM2008地球重力模型进行的大地水准面计算、重力位计算、不同尺度重力场分析计算等将更为精确。

2　GPS高程拟合

如图1所示，H为大地高，Hg为正高，Hr为正常高，hg为大地水准面到地球椭球面的距离，ξ为似大地水准面到地球椭球面的高差，叫做高程异常。

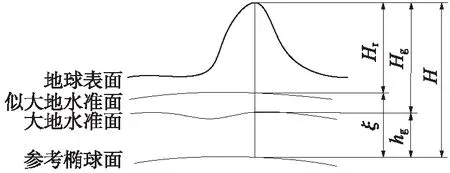
图1　高程异常

GPS测量的参考椭球体位WGS-84椭球，测得的大地高H是基于WGS-84椭球表面的大地高H84，我国铁路勘测中采用的国家1985高程基准的85高程H85是基于似大地水准面的正常高Hr，这种WGS-84椭球面与似大地水准面之间的差距叫高程异常，可表示为

ξ=H-Hr=H84-H85

通常采用GPS高程拟合的方法获取这些正常高，因此计算出精度可靠的高程异常十分重要。GPS高程转换的基本原理是通过测得GPS点的大地高和已知该GPS点的正常高获得该点的对应高程异常值。由于高程异常在小区域范围内的变化相对平缓，可以用一些拟合的方法对区域内的高程异常值进行估计，然后利用已知点正常高计算出拟合系数，求出待定点的高程异常值，进而获得该点的正常高。

3　基于EGM2008模型的GPS高程拟合方法

在以地球质心为坐标原点、Z轴与地球自转轴相重合坐标系中的球坐标中，以r表示向径，θ表示纬度，λ表示经度，由Bruns公式可以推导出地球表面上任意一点P的高程异常

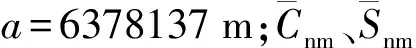
根据物理大地测量学的理论，高程异常可表示为

ξ=ξGM+ξΔG+ξT

其中ξT表示短波部分，可以通过求解地形改正得到；ξΔG为中波部分，可以通过求解重力异常的边值得到；ξGM为长波项，可由重力场模型计算出[4]。采用基于EGM2008地球重力场模型中的重力场中长波信息可以求解ξGM项，而其中的中波、短波部分可通过GPS测量中若干已知正常高的GPS点逼近，拟合出其他点ξΔG、ξT两项值。

基于EGM2008模型的GPS高程拟合方法在实际工程应用中具体步骤可概括为：

①求取GPS点高精度的WGS84平面坐标及大地高H84。在实际工程中，可以通过建立GPS网，并与IGS站联测来实现。

②利用EGM2008地球重力场模型求解由重力场模型所计算的各GPS点高程异常的长波项ξGM。

③利用GPS网中部分已知正常高的GPS点，通过GPS高程拟合的方法拟合出未知正常高的GPS点正常高Hr。

4　算例分析

某新建铁路工程位于天山南麓，线路长度约130.5 km。线路起点、终点位于两条国道附近，能收集到已知正常高的GPS点；其间线路穿越约80 km的无人区，无控制点资料。测区最低处海拔约1 600 m，最高处海拔约3 700 m，平均海拔约2 500 m。勘察初期，沿线路方向建立了CPI控制网[5](带状的四等GPS网)，全网共计40个CPI点；并在线路约0 km、12 km、100 km及130 km处联测了已知正常高的GPS点；勘察中期，采用16台Dini12电子水准仪，按三等水准作业要求对全部CPI点进行了水准测量；工程控制网及联测情况如图2所示。通过传统的GPS高程拟合与基于EGM2008地球重力场模型的GPS高程拟合实验，根据拟合的高程结果和几何水准成果进行统计分析，得出了一些结论。

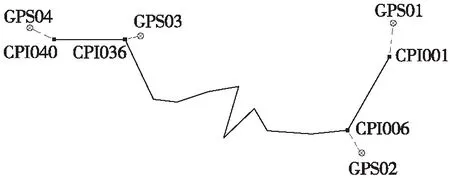
图2　工程控制网及联测情况示意

4.1　传统GPS高程拟合

先按照传统的GPS高程拟合的方法进行高程拟合。由于4个已知正常高的GPS点位于GPS网两端，网段中间大于80 km无约束点。采用首末两个已知正常高的GPS点约束拟合时，离起算点远的CPI点拟合高程与几何水准高程之差最大达1 137 mm；用四个已知正常高的GPS点约束拟合时，离起算点远的CPI点拟合高程与几何水准高程之差最大达1 654 mm。传统的GPS高程拟合不能满足测量要求，且离起算点越远差值越大，约束点间距越远差值越大(如图3所示)。

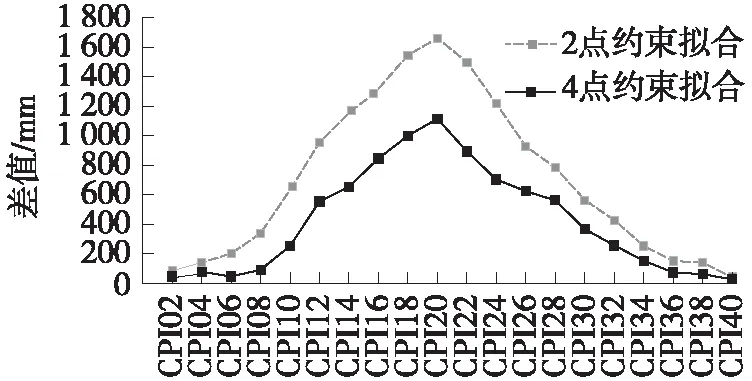
图3　传统GPS高程拟合结果与几何水准高程比较

4.2　基于EGM2008地球重力场模型的GPS高程拟合

采用基于EGM2008地球重力场模型的GPS高程拟合时，先根据GPS网测得的高精度WGS84平面坐标及高精度的大地高H84，解算出高精度的WGS84三维坐标，故能得到高精度的WGS84椭球大地高。利用EGM2008地球重力场模型求解由重力场模型所计算的长波项ξGM(如表1所示)。

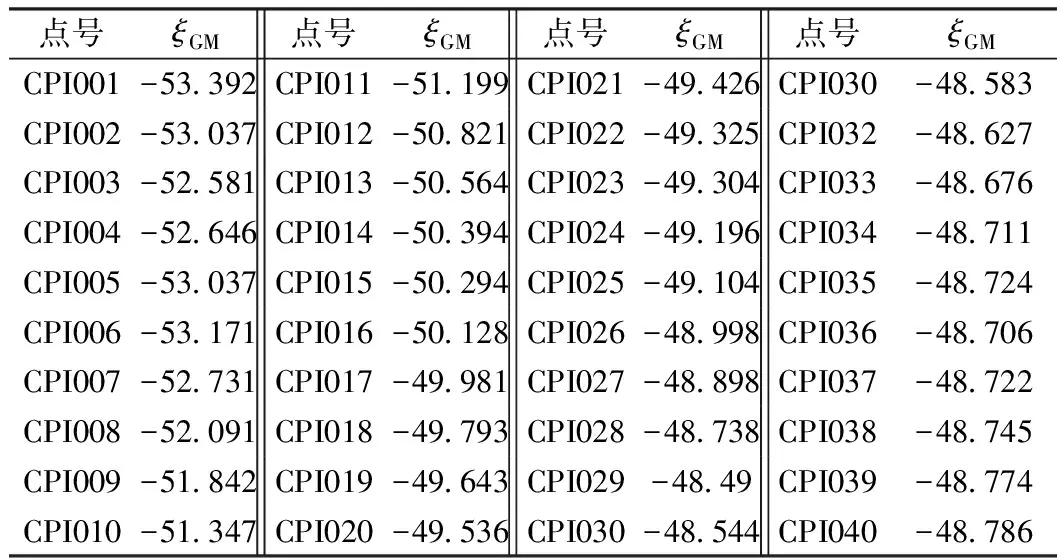
表1　各CPI点高程异常长波项　m

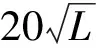
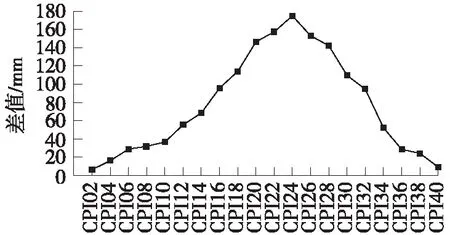
图4　基于EGM2008模型的GPS拟合高程与几何水准高程比较

5　结束语

利用基于EGM2008模型的GPS高程拟合方法进行高程拟合可以明显提高高程拟合的精度，拟合精度可以达到四等精度要求。

利用基于EGM2008模型进行GPS高程拟合，已知水准点的间距可以放宽至80 km左右。不同地区的已知水准点间距有待进一步研究。

采用基于EGM2008模型进行GPS高程拟合时，需要采集较高精度拟合点的WGS84椭球大地高。

[1]Pavlis N K，S A Holmes，S C Kenyon，et all.An Earth GravitationalModeltoDegree 2160: EGM2008[R]. Presented atthe 2008 General Assembly of the European Geosciences Union， Vienna， Austria， April， 2008:13-14

[2]章传银，郭舂喜，陈俊勇，等.EGM2008地球重力场模型在中国大陆适用性分析[J].测绘学报，2009，38(4)：283-289

[3]魏子卿，王刚.用地球位模型和GPS/水准数据确定我国大陆似大地水准面[J].测绘学报，2003，32(1)：1-5

[4]陈俊勇.高精度局域大地水准面对布测GPS水准和重力的要求[J].测绘学报，2001，30(3)：189-192

[5]TB10101—2009铁路工程测量规范[S]

[6]胡明城.现代大地测量学的理论及其应用[M].北京：测绘出版社，2003

[7]武鹏.GPS拟合高程应用于铁路定测的研究[J].铁道勘察，2009，35(6)：11-13

[8]孙风华，吴晓平，张传定.我国1′×1′高程异常模型的建立及应用[J].地球物理进展，2005，20(4)：986-990

[9]夏哲仁，石磐，李迎春.高分辩率区域重力场模型DQM2000[J].武汉大学学报：科技信息版，2003，28：124-128

[10]左虎，范东明.GPS高程转换的新方法[J].铁道勘察，2006，32(6)：6-8