子午线收敛角变化规律及其在贯通定向中可靠性应用研究
2020-09-03贺清清刘梦颖王明明
贺清清,徐 彬,李 昊,刘梦颖,王明明
(如东县自然资源局,江苏 如东 226400)
在贯通定向工程中,陀螺仪的作用是通过在地面已知高精度控制边上进行量测,获取陀螺观测数据后,联系地面上下边的子午线收敛角常用测量学计算公式,经过公式计算后可以获得地下待测边在相关分带中的高斯投影坐标方位角;根据子午线收敛角的变化分布概略情况,为计算方便,在用常用测量学计算公式计算子午线收敛角时,存在子午线收敛角计算残差情况;但是具体在各个分带投影中,子午线收敛角残差变化规律以及残差影响数值,以致对相关高精度隧道贯通的相对影响及应用适应性如何,目前研究的比较少;并且由于井上下有的控制边的部分点布设成了普通全站仪强制对中台,陀螺仪定向时仪器不得不安置在部分缺少平面坐标的对向点,最后的子午线收敛角计算不得不使用另外一个点的坐标;因此陀螺定向边两点之间的距离及方向对子午线收敛角变化的影响规律也需要深入的研究[1]。
1 陀螺全站仪定向及子午线收敛角的应用计算
1.1 陀螺全站仪定向过程及相关计算
陀螺全站仪在定向过程中,综合考虑精度及经济适用性,一般采用的是3+3+3方式进行定向,即在井下仪器常数定向边进行三测回的定向,井下待定向边进行三测回的定向后,测后再在井上仪器常数定向边进行三测回的定向[2],通过陀螺定向陀螺方位角计算待测边坐标方位角,如图1所示。
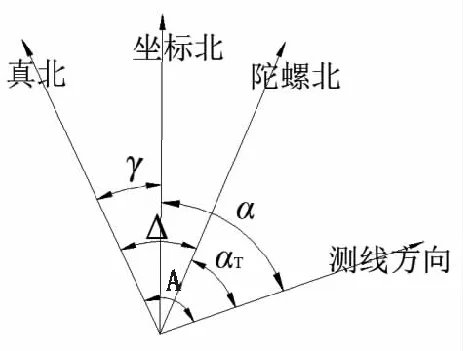
图1 陀螺定向示意图
图中,αT为定向边所测陀螺方位角;Δ为定向区域的陀螺仪仪器常数;A为陀螺定向边的真北方位角;γ为陀螺仪安置点的子午线收敛角;α为定向边测线方向坐标方位角。
假设地面仪器常数定向边测线方向已知坐标方位角为α0,陀螺全站仪安置点子午线收敛角为γ0,仪器在该常数定向边测得的陀螺方位角为αT0,设陀螺全站仪的仪器常数为Δ,则Δ=α0+γ0-αT0
(1)
(2)
如上式(2)可知,井下待测边的坐标方位角测定计算值,与常数定向边及井下待测边陀螺全站仪安置点的子午线收敛角差值有关,对于高精度的陀螺定向,必须考虑两边陀螺定向安置点子午线收敛角的差值影响,并探求相关影响规律[3]。
1.2 常用子午线收敛角计算公式分析
(1)赫里斯托夫七次项计算公式
(3)

(2)测量学近似公式
子午线收敛角的计算公式相当于取式(3)的第一部分,即
γ=sinBl
(4)
(3)平面坐标计算子午线收敛角
平面坐标子午线计算公式其实是基于公式(3)的另一种形式,计算公式如下
(5)
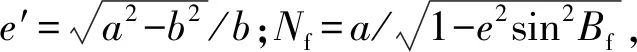
(4)工程测量近似计算公式
工程测量近似计算公式其实是对式(5)仅取第一项的结果,计算公式如下:
(6)
(5)矿井常用子午线收敛角计算公式
γ=Ky
(7)
式中,γ为子午线收敛角,以分为单位;y为点的横坐标,km;K为系数,以纵坐标x(以km计)为引数由表查取。
2 不同分带投影下子午线常用收敛角计算残差极值及对贯通定向影响分析
2.1 常用子午线收敛角计算公式残差变化一般规律分析
由式(3)及式(4)可知,子午线收敛角计算可以使用点位的经纬度,也可以使用点位的平面坐标,而两个公式是对等计算公式的两种形式[4];根据子午线收敛角的严密计算式(3)可知,子午线收敛角计算值是经差l的奇函数,在中央经线以东为正,在中央经线以西为负,且在同一纬度上,经差越大,子午线收敛角越大;同一子午线上,纬度越高,子午收敛角也越大[5]。式(3)的赫里斯托夫七次项计算公式计算的精度可达到0.001",根据式(3)和简易计算式(4),得出子午线收敛角一般测量学计算公式的残差A为:
(8)
由上式可知,在纬度既定的情况下,子午线收敛角测量学计算公式较严密计算公式计算残差随着点位的经差的增大而增大,具体考虑到高斯投影一般最大带宽为6°带以及必要的分带控制点重合情况,选取最不利的经差为l=3.5°为区间,使用MATLAB软件程序,图示化子午线收敛角测量学计算公式残差分布情况,如下图2所示。
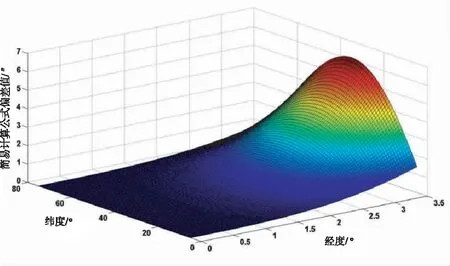
图2 简易计算公式子午线收敛角计算残差
由上图可知,当点位纬度一定时,子午线收敛角计算残差随着点位离分带中央经线的经差的增大而增大,并且残差变化越来越剧烈;当点位经度一定时,子午线收敛角计算残差随着纬度的增大先增大后变小,在中纬度地区残差值达到最大,并且随着经度的增大,这种残差影响值越来越不可忽略不计。
2.2 6°带子午线收敛角计算残差最大值及影响分析
由赫里斯托夫七次项与简易公式差值式(8)的特性,结合图2的相关结论,发现在高斯投影6°带分带投影中,简易公式子午收敛角计算差值在经差3.5°端点处取得最大值;取相应经差截面,得出子午线收敛角简易计算公式计算残差值变化情况如下图3所示。
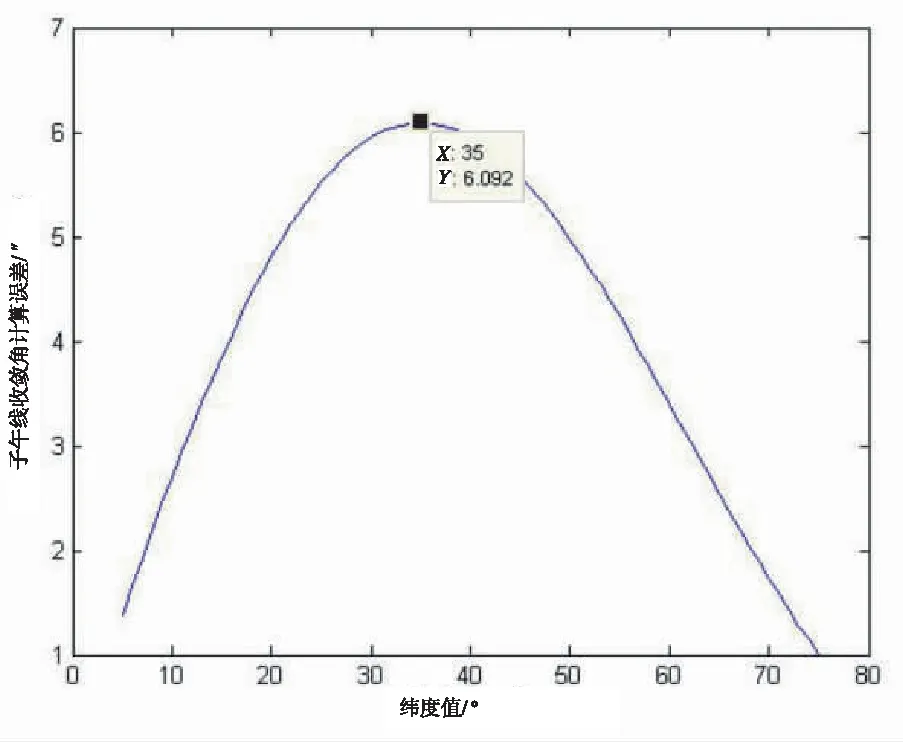
图3 经差为3.5°时简易计算公式计算子午线收敛角残差
由上图3可知,在6°带中,在取极限经差3.5°的基础上,当纬度为35°时,简易计算公式子午线收敛角计算残差达到最大值6.092″;假设在实际工程运用中,考虑一个隧道区间相邻两开挖孔洞距离长度为4 km,横向贯通误差限差为100 mm,则此残差引起的贯通定向横向误差为118.1 mm,简易公式适用性极差;当然目前分带一般使用的是3°带分带,因此,对子午线收敛角计算残差在3°带中的极致研究更加重要[6]。
2.3 3°带子午线收敛角计算残差最大值及影响分析
由图2可知,纬度既定的时候,子午线收敛角简易计算公式的残差随着经差增大而增大;在高斯投影3°带分带中,取极限经差为1.75°,取相应函数截面,最终此极限经差条件下,子午线收敛角计算残差值变化情况如下图4所示。
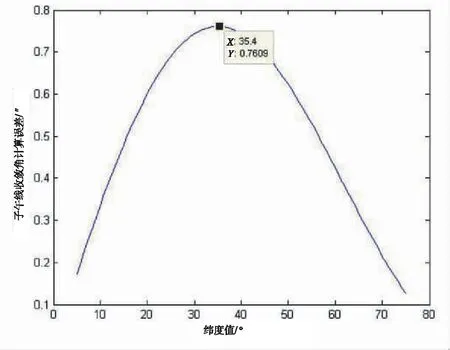
图4 经差为1.75°时简易计算公式计算子午线收敛角残差
由上图4可知,在3°带分带中,在取极限经差1.75°的基础上,当纬度为35.4°时,简易计算公式子午线收敛角计算残差达到最大值0.760 9″;假设在实际工程运用中,考虑一个隧道区间相邻两开挖孔洞距离长度为4 km,横向贯通误差限差为100 mm,则此残差引起的贯通定向横向误差为14.8 mm,按照控制边影响1/3原则,简易公式适用性好,说明在3°带分带中,从残差绝对影响量方面,可以使用子午线收敛角测量学简易计算式[7]。
2.4 子午线角简易计算公式残差相对影响量分析
这些简易公式与子午线收敛角计算精度达到0.001"的赫里斯托夫七次项计算公式相比较,在3°带分带边缘经度1.75°、纬度35°处有最大差值为0.76";且由式(8)赫里斯托夫余项A对简易公式进行相比,得到的相对影响量如下图5所示。
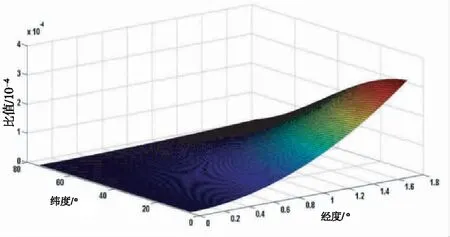
图5 子午线收敛角计算余项相对影响量
如图5所示,在余量影响最大处,也仅仅只有104级,因此在3°带分带的任何一个区域,可以通过简易公式进行子午线收敛角变化规律及应用研究。
3 局部地区子午线收敛角变化梯度规律分析及应用
3.1 子午线收敛角变化梯度规律分析
在实际应用中,有时候由于观测条件限制,只能在陀螺定向边某一端点进行陀螺定向,而恰好此端点暂时没有平面坐标值(例如某些高精度GPS网点全部设置的是强制对中装置,陀螺无法安置进行仪器常数观测,且暂时不可能立即测设新点坐标);并且很多工程井下定向边陀螺安置点位与地面仪器常数定向点距离较近,两点间子午线收敛角的差值影响将会导致系统误差传入井下定向边,因此有必要考虑点位相互之间的距离及方位在各个经纬度位置对子午线收敛角的具体影响及规律[8]。
根据子午线收敛角简易计算公式(4),子午线收敛角值和经纬度有关,根据方程梯度公式,子午线收敛角在经纬度面的变化梯度为
(9)
我国领土最南部的南海南沙群岛中的曾母暗沙,处于纬度北纬4°附近;最北方漠河以北黑龙江主航道的中心线为界限,处于纬度北纬53°附近。根据式(9),同样纬度的情况下,经差越大,南北纬度方向影响量越大,因此在3°带分带边缘l=1.5×3 600=5 400"前提下,设梯度分量比值
(10)
当B=5°时,上式b=3.34,此时在纬度为5°的3°带边缘地带,纬度变化对子午线收敛角的影响达到最大,约为经度方向的1/3不到;在北纬15°以北地区,点位的子午线收敛角变化梯度在经度方向影响量至少为纬度方向的10倍以上。
因此,由式(10)结果及上述结论得知,在我国大部分范围内,子午线收敛角变化总体上是东西经度方向变化较南北纬度方向变化剧烈得多。
3.2 基于子午线收敛角变化规律的陀螺定向边选取影响分析
联系式(8),运用MATLAB软件,假设两定向点Δx=0,且Δy为变量时,两定向点的子午线收敛角差值如下表1所示。
根据子午线收敛角简算公式,在用高斯投影的3°带分带内,我国区域内的子午线收敛角最大值约为1.2°。因此可以认为在分带投影区间内各点坐标xy南北、东西方向和经纬度方向接近一致。
由表1及式(9)可知,在3°带中各个既定纬度条件下,同等边长的两点之间的子午线收敛角差值与两点所处经度无关,两点之间处于东西方向时,子午线收敛角差异较大[9]。以徐州所处北纬35°为例,在东西100 m长的边上子午线收敛角差值达到2.26",在500 m长的边上差值达到11.28"。使用5"~10"的陀螺全站仪定向时,不能忽略两点因东西方向距离较大引起的此子午线收敛角差值。
当两定向点为变量时,两定向点收敛角差值如下表2所示。
由表2可知,当两定向点位于南北方向时,两点之间的子午线收敛角差值比较小。以实际工程为例,仪器常数定向点和井下点距离一般都在500 m以内,此南北方向的距离引起的子午线收敛角差值最大为0.42";在徐州地区,南北方向500 m的距离子午线收敛角差值也只有0.35",对于高精度仪器及方案设计施工的影响可以忽略不计。
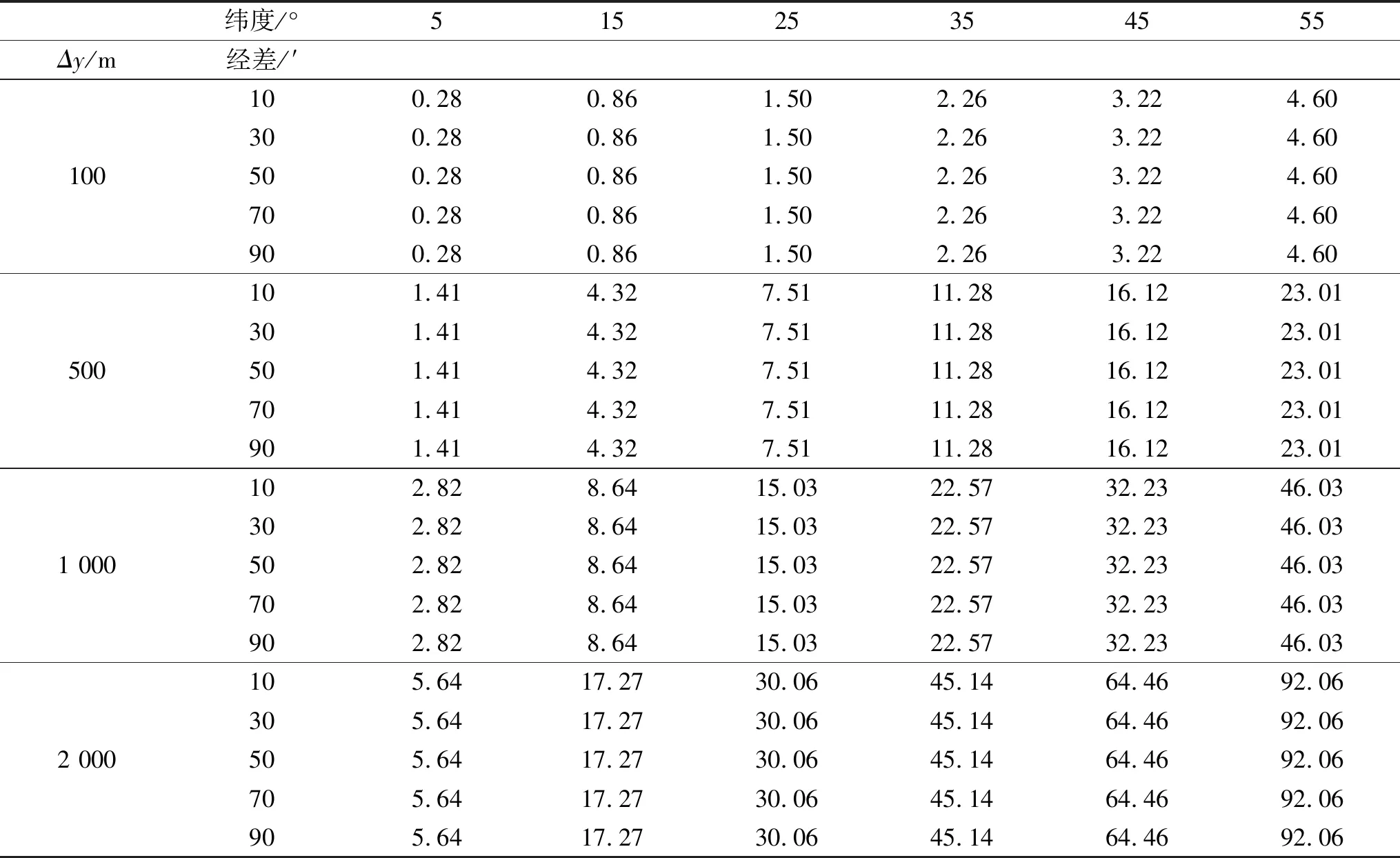
表1 Δx=0,且Δy为变量时,子午线收敛角差值/"
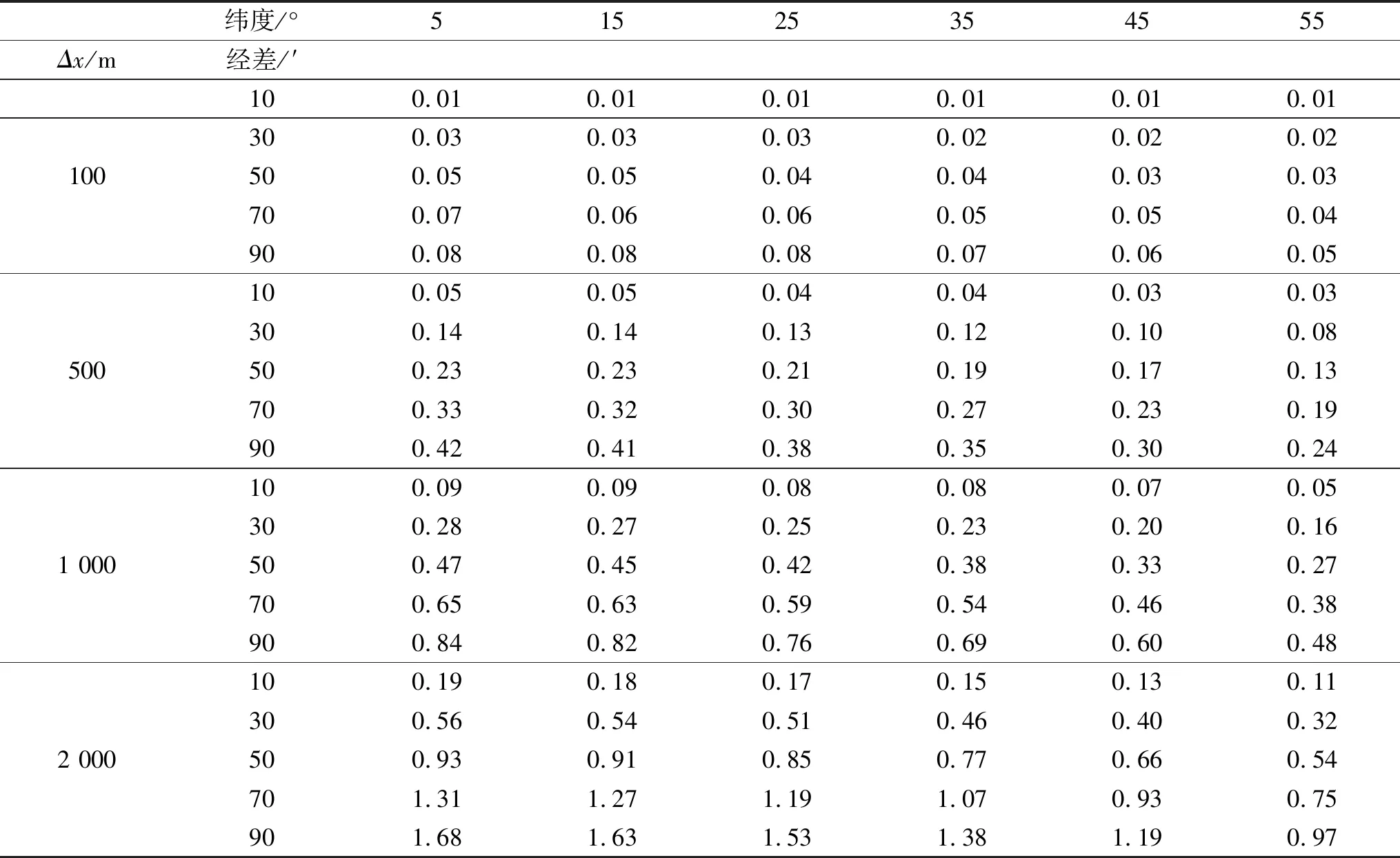
表2 Δy=0,且Δx为变量时,子午线收敛角差值/"
3.3 基于子午线收敛角变化规律的贯通定向边布设可靠性应用分析
3.3.1 境内煤炭学子午线收敛角简算公式可靠性应用分析
因此在实际运用中,一般对于煤矿常用的子午线收敛角差值计算式δγ=32.23tanB(y0-y),根据式(10)及相关结论,在国内范围内陀螺定向边进行陀螺定向时,一般纬度变化引起的子午线收敛角变化介于经度变化引起的子午线收敛角变化的1/39~1/3;对于我国境内而言,煤炭资源几乎都分布在中纬度以上,此时,纬度变化引起的子午线收敛角变化相对经度来说都小于1/10;考虑到现行的矿井贯通及后续控制定向中,一般使用的都是5"~10"陀螺全站仪,联系2.4结论,简易公式计算残差不到1",煤矿常用子午线收敛角计算中纬度影响导致的二次残差不到0.11"。因此,针对现行国家通用的2000坐标系下的3°带高斯投影中,我国国内煤矿常用子午线收敛角计算公式精度能完全保障煤矿贯通及定向控制测量中高精度要求,并且联系2.4及3.1相关结论,可以作出严格残差评定的结果要求。
3.3.2 子午线收敛角变化规律在轨道交通定向边布设应用分析
所以针对煤矿常用的平面坐标子午线收敛角差值计算方法,大部分时候,尤其在中纬度及以上区域,从绝对及相对精度上来说,都是极其适用的。在实际工程中,要充分考虑仪器常数定向边及井下定向点的距离及方位关系;当井上下点距离在500 m范围内时,点位相对位置在近似南北方向时,可以忽略子午线收敛角差值,其他情况下必须要分别计算;另外,城市轨道交通贯通定向中,在4 km的区间段,横向贯通限差为10 mm,根据2.3结论,也可以在一般的3°带任意处使用简易计算公式进行子午线收敛角或者是子午线收敛角差值计算;并针对子午线收敛角变化梯度规律,设计具有相应方向和位置的控制边及定向边,联立高精度测量机器人及巷道内双向贯通的交叉导线同时进行高精度二次控制测量,满足贯通定向面的横向精度要求。而目前,在一些城市地铁建设中,使用的一般是独立坐标系,点的平面坐标短时间难以获得,因此可以通过手机GPS软件进行GPS定位获取大地坐标并使用简易公式进行子午线收敛角计算,使用大地坐标简易计算公式时,在3°带边缘地区,计算最大误差仅仅也只有0.48"。可以使用手机中的GPS工具箱软件,经纬度定位都在亚秒级,平面20 m以下,根据式(9)梯度公式,考虑计算公式误差,最后反映在子午线收敛角的计算精度也肯定在1"以内。但此类坐标方位角是基于84椭球计算的,后期需要通过坐标转换将结果转换到待使用坐标系中[10]。
4 结 论
(1)本文将测量学常用子午线收敛角计算公式与赫里斯托夫七次项严密计算公式进行对比,发现残差相对影响量只有10-4量级;但是在6°带分带,尤其是纬度35°边缘投影处,因为简易公式残差带来的子午线收敛角计算误差达到最大,数值达到6.092″,在4 km贯通隧道上的影响达到了118.1 mm,误差很大;而在3°带分带,尤其是纬度35.4°边缘投影处,因为简易公式残差带来的子午线收敛角计算误差达到最大,数值达到0.760 9″,在4 km贯通隧道上的影响达到了14.8 mm,相对100 mm的贯通误差要求几乎可以忽略不计;
(2)本文基于经纬度方向,进行了子午线收敛角变化梯度计算分析,对比发现在国内范围内,从南到北区域里,基于某区域内陀螺定向的定向点的子午线收敛角变化差值都集中在经纬度,也就是大致东西方向;而纬度变化导致的子午线收敛角变化较经度来说只有1/39~1/3,在纬度15°以上区域,就已经达到了1/10;考虑到地面及地下控制边,有时候因为一些强制对中点存在无法安置陀螺全站仪,其他点可以参考此次研究成果,联系定向点之间相互距离及方向,设计控制及定向边,应用此次具体研究的子午线收敛角变化规律。
