基于FEM的板料回弹预测与补偿研究进展

王广凯，成思源，李苏洋，张家访，2，张湘伟

(1.广东工业大学机电工程学院，广东广州510006;2.中国科学院深圳先进技术研究院，广东深圳518055)

回弹是汽车外覆盖件成形过程不可避免的物理现象[1]，由于在成形过程中既存在塑性变形，又存在弹性变形，卸载后由于弹性变形的恢复，即产生回弹现象。零件的最后回弹形状是其整个成形历史的累积效应，而板料成形过程与模具几何形状、材料特性、摩擦接触等众多因素密切相关，所以板料成形的回弹问题非常复杂。

由于对汽车轻量化设计的要求不断提高，高强度钢板材料占汽车车身的比重越来越大。然而用一般冲压方法生产出的高强度钢零件形状往往不在误差允许范围控制内，不能适合实际的应用，车身零件回弹对车身品质的影响日益突出。国内外许多汽车公司正在开展“2 mm”工程，这无疑也增加了对冲压件成形精度的要求。现代制造业要求在设计阶段就能解决产品整个生命周期所遇到的所有问题，过去基于经验和反复工艺实验的回弹控制方法显然无法满足这样的要求，未来解决回弹问题的主要途径应该在于数值模拟技术[2]。冲压成形中的回弹问题一直是研究的热点和难点，目前回弹的预测、测量、控制及补偿的研究还只是处于初级水平[3]。从20世纪70年代FEM仿真开始应用于回弹问题以来，众多学者进行了深入的研究，文中着重介绍FEM 在回弹预测和回弹补偿的应用与发展。

1 FEM 在回弹预测中的应用与发展

对回弹变形做出准确预测是有效控制回弹缺陷的前提。长期以来，人们在回弹预测方面做了大量的工作，常见的研究方法有解析法、实验法和有限元数值模拟方法[1]。但是解析法难于处理复杂三维冲压件的成形回弹问题。实验法使用也具有局限性，不仅受实验条件的影响，还与实验数据的处理方法、经验公式的应用条件等许多因素有关，并且一种经验公式只适用于实验状况相当接近的生产过程。但是解析法和实验法的研究为用有限元法解决回弹问题提供了一定的理论和实验支撑。而有限元法可以很好地弥补解析法和实验法的不足，随着有限元技术的不断进步，它在回弹预测方面的应用取得了快速的发展，在材料模型、单元类型、接触处理和FEM算法方面都有许多的成果，也得到越来越多研究者的关注。

(1)材料模型方面。有限元模拟的准确性在很大程度上取决于材料的本构关系能否真实地反映材料真实的力学特性。目前板料成形常用的是弹塑性材料，具有明显的各向异性，因此采用一种能充分体现板料面内各向异性的弹塑性材料模型非常重要。屈服准则是本构关系的重要内容，对屈服准则的研究成为研究板料成形的关键问题之一。20世纪60年代末开始，各向异性材料的屈服行为成为各国学者研究的热点，很多各向异性屈服准则被相继提出。HILL 在1948年提出Hill’48 各向异性屈服准则，在随后的数十年内针对剪应力分量、厚向异性系数r 等问题，他又进行了多次改进，提出了多个各向异性屈服准则，成为了其他学者的研究基础。1989年，BARLAT等[4]提出了能较好地描述板料面内各向异性的Barlat’89 屈 服 准 则。随 后，虽 然 Barlat’91[5]、Barlat’97[6]和Barlat’2003[7]等相继被提出，但是由于参数的复杂性及缺乏足够验证还没有得到广泛的应用。在HILL 和BARLAT的屈服准则研究基础上，很多新的屈服准则被不断地提出。柳玉起等[8]在平面各向异性三参数Barlat-Lian 屈服准则的基础上加入两个横向剪切应力分量σxz和σyz，提出一个改进的5参数Barlat-Lian 屈服准则，结合BT或BWC 壳单元，模拟了板料在成形过程中的各向异性行为。陈志英等[9]基于Hill’48 各向异性弹塑性屈服准则，发展了可以用来描述各向异性多孔延性材料损伤演化发展的GTN弹塑性细观损伤本构模型，将材料的塑性各向异性行为和损伤发展有机地耦合起来，从而可以同时描述材料的弹塑性行为和损伤演化规律。

在材料的强化模型方面，由于冲压成形所用板料不是理想弹塑性材料，它具有硬化效应，所以后继屈服函数与初始屈服函数不一致，需考虑其强化模型。材料强化模型通常有等向强化、随动强化和混合强化3种[3]。一些研究通过这3种模型的模拟与实验对比[10－13]，发现最适合用于板料回弹模拟的是非线性混合强化模型，这种模型结合了等向强化和随动强化的特性，充分体现了循环加载时的包申格效应。用此模型作出的回弹预测结果与试验测量结果十分吻合[10]。建立考虑板料反向加载过程中包申格效应的各向异性材料强化模型是未来的发展方向。

另外，先进高强度钢、铝镁合金等高性能材料目前已广泛应用于板料冲压生产中，这些新材料的工艺特性、成形规律、内部组织等与传统钢板存在很大区别。所以在实际应用中带来更多的成形与回弹问题。李光耀等[14]在高性能材料本构关系及基础参数获取方面做了较为详尽的论述。利用更加科学的实验方法获取能反应板料实际加载特征的模型对提高数值模拟的准确性有着重要的意义。

(2)单元类型和尺寸方面。板料成形数值模拟分析发展过程中，出现过薄膜单元、实体单元、壳单元、实体壳单元等单元类型。目前，在板料冲压成形有限元数值模拟分析中，通常采用壳单元。该类单元位移和转动各自为独立函数，表达格式简单。采用壳单元离散板料可使之简化为二维问题，板料平面的单元尺寸不受板厚限制，从而可以减少单元数量、缩减计算量且可以避免因刚度矩阵元素间相差过大而导致求解困难。但在分析板料厚度较薄的冲压成形及回弹问题时，易于产生剪切锁死问题。Hughes-Liu (HL)壳单元和Belytschko-Tsay (BT)壳单元是应用得最广泛的壳单元模型。近年来，新型的单元类型不断被提出，尤其是实体壳单元。BüCHTER[15]和 SANSOUR[16]提出了七参数壳单元，每个节点需7个自由度，考虑了壳单元厚度方向上的应力应变。一些研究者[17－18]结合壳单元和实体单元的优点提出了实体壳单元，该单元突破了传统壳单元的限制，考虑了壳单元厚度方向的应力和应变，不含转动自由度，这给处理实际问题带来了很大的方便，特别是大变形分析问题。LI 等[19]通过实例比较了实体单元和壳体单元，建议半径厚度比(R/t)在5～6以上，选用壳单元;在5～6之下，选择实体单元。ALVES de SOUSA等[20]提出了一种选择缩减积分实体壳单元RESS，并用于线性和非线性分析。许江平等[21]提出了一种新型的八节点实体壳单元(MSSS)，在厚向划分一层网格，采用多点积分获得了厚向应力应变分布，采取黏性沙漏控制算法，克服了零能模式，用来模拟板料成形、回弹现象。但该单元类型处理静态问题的效果未加证明。

(3)接触处理方面。板料成形与回弹的整个过程中，模具与板料之间就在不断地发生接触变化，接触界面之间的相互作用的准确模拟对回弹模拟结果的可靠性至关重要。接触处理中的主要问题包括接触面的搜寻、接触力的计算、摩擦力的计算。在有限元法中，接触面实际上被离散而由接触点的组合来代替，因此，接触面的计算就转化为接触点的搜寻，其实质就是对板料上任一节点找出与之接触点的位置。最常用的搜索方法有基于解析曲面的一次搜索法[22]、针对有限元网格和参数曲面的主从搜索法[23]以及非参数曲面的级域搜索法[24]等。然而至今各个方法仍然存在一些问题，例如有限元网格描述的模具型面接触搜索简便，但计算稳定性较差;基于参数曲面描述的模具型面接触搜索的计算稳定性良好，但接触求交计算存在收敛性问题。有些学者在上述搜索算法的基础上提出了新的改进方法，提高了计算效率[25－29]。

目前接触力计算常用的算法有拉格朗日乘子法和罚函数法，它们的共同点在于将有约束条件的变分问题转化为无约束条件的变分问题。拉格朗日乘子法模拟出的结果更为准确，但是计算效率较差，而且对于变形大的单元容易造成收敛困难。罚函数控制方程的阶数和带宽都小于拉格朗日乘子法，但是罚函数法因子的取值对计算结果精度的影响很大。

2018年11月8日下午3时，随着汽笛声传来，由白俄罗斯开往重庆的第三趟传化乳制品直达班列顺利抵达团结村中心站。该班列由41个集装箱组成，满载白俄罗斯优质乳制品，全程8000多公里，历时12天。这是继今年首趟重庆直达白俄罗斯班列开通后双方的再一次深入合作，也是白俄罗斯到中国的首个整装班列，当天举行了隆重的接车活动。

在摩擦力计算方面，人们常用经典库仑摩擦定律来计算摩擦力，但是板料冲压成形中采用经典库仑定律会带来数值稳定性问题[3]。不少学者对库仑定律进行了修正[3，22]。

(4)FEM算法方面。一般分为静态隐式算法、动态显式算法和显/隐结合算法。静态隐式算法在计算大型成形问题时收敛性差、效率低，计算量大，但进行回弹计算时效率很高。动态显式算法无收敛问题，算法效率高，且无需建立总体刚度矩阵，是求解板料成形问题的有效方法，但对于回弹计算效果并不理想。WANG 在板料回弹预测、测量可靠性及补偿技术研究现状中指出，显/隐式相结合的方法是处理板料成形回弹问题的有效方法[13]。陈喜娣等[30]用显/隐结合法进行了成形与回弹研究，对材料厚度、件变形量对回弹的影响进行了分析，板材成形是一个相当复杂的过程，既有弹性变形，又有塑性变形，一般属于动态接触问题，如果采用隐式算法，收敛就难以保证(特别是出现失稳起皱时)，即使收敛，耗费CPU时间也很长。而显式算法因不涉及收敛问题，无需构造刚度矩阵就可以完成求解。动态显式算法模拟板材成形过程效率很高，但若进行回弹计算则非常困难。回弹是冲压后的卸载过程，可简化为非接触问题，这时，即使采用隐式算法，也不会出现收敛困难，计算时间不会很长。这样，回弹过程的模拟就变成求解存在初应力的变形体的静力平衡问题。采用动/静态联合算法求解，能极大地提高回弹计算效率和精度。

2 基于FEM的回弹补偿的研究进展

板料冲压成形过程中的回弹是卸载过程产生的反向弹性变形，是一种普遍存在的物理现象。对于回弹问题常用的方法有两种:(1)通过工艺参数的控制，如设置合适的拉延筋和压边力等，来减少回弹量;(2)进行模具补偿，即在考虑回弹量的基础上，对模具型面进行相应的补偿，使得冲压件回弹后的形状刚好满足设计要求[31]。第一种方法没有从根本上解决回弹量的问题，它只是在一定程度上减少回弹量。第二种方法的实施有3种常用的方式:(1)在实际生产中反复试冲，然后根据试冲件和设计模型的差别进行模具型面的修整。为了实现实际模型和设计模型的比较，在生产中一般先根据设计模型制造出检具，然后将实际冲压件套在检具型面上进行比较，工人结合检验结果和自己的经验对模面进行修整。(2)实际冲压完之后，借助三维扫描仪获取回弹后的零件形状，通过某种手段与目标零件对比，获取回弹量，然后根据该回弹量对模具型面进行修正，从而得到满足精度要求的冲压件。(3)获取冲压件的CAD模型后，板料的成形、回弹、补偿全都利用FEM 进行，用最终获取的补偿后的模具型面，进行生产获得需要的零件。FEM可以应用到方式2 和3的回弹补偿中，要取得良好的补偿效果，需要得到精确的回弹量，以及高效的补偿算法。下面从这两个方面进行论述。

2.1 回弹测评方面

应用有限元数值模拟技术对回弹补偿进行研究是目前及今后解决回弹问题的重要手段，但进行回弹补偿的前提是获取精确的回弹量。龚志辉等[32]提出一种基于逆向工程技术的回弹评测方式，对实际冲压件进行激光扫描后重构出型面，根据弹性变形的特点对模型进行强制变形以找到节点的对应关系，并根据模型的几何中心计算出曲面的重合点，以对应节点的距离为适应度函数利用遗传算法搜寻出最佳旋转位置，并计算出各节点的法向偏移距离作为该节点的回弹量。邵鹏飞等[33]采用动力显式有限元计算程序MSC/DYTRAN，采用动力松弛法模拟了板料成形及回弹过程，计算出板料成形后的回弹量，并应用于回弹补偿。邹付群等[31]利用软件Geomagic Qualify 对冲压件的点云数据和CAD模型进行3D 比较、2D 比较和边界比较，分别检测了冲压件的整体、重要截面以及边界的回弹情况，并将检测结果以图文方式直观显示出来。

2.2 补偿算法方面

基于FEM的回弹补偿是依据所测得的回弹引起的位移或内力，运用一定的补偿算法直接对形状进行修改获得模具型面，所以补偿算法的优劣会直接影响回弹补偿的精度，也成为回弹问题的一个研究重点，被国内外众多学者持续深入地研究。WEBB 等[34]提出了一种用于过程控制的DTF法，借助实验设备获取回弹后模面的坐标数据，将模具形状和零件形状通过傅里叶变换转至频域，然后通过建立实验模具形状和目标零件形状之间的传递函数来计算模具的补偿型面，再利用新模面冲压零件，测量回弹后的曲面与零件形状比较，如果误差在允许范围之内则停止，否则迭代此过程则获得最终型面。其控制过程如图1所示。

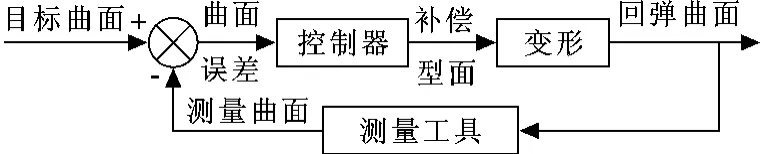
图1 DTF控制过程图

KARAFILLIS 等[35]提出了基于有限元技术的FDM法(Force Descriptor Method)，通过有限元法计算板料在每次成形仿真结束时的内力，然后将该内力反向施加在此次成形的模具形状上，来获得补偿后的新模具型面，将此过程迭代至回弹量达到误差范围之内。该方法在经过2～3次迭代之后，可以减小回弹误差90%以上。FDM法的一个缺点是:由于直接将成形后的内力反向施加到此次成形的模具型面上，一旦出现“反向”现象，将导致计算的不收敛。该算法迭代流程图如图2所示。

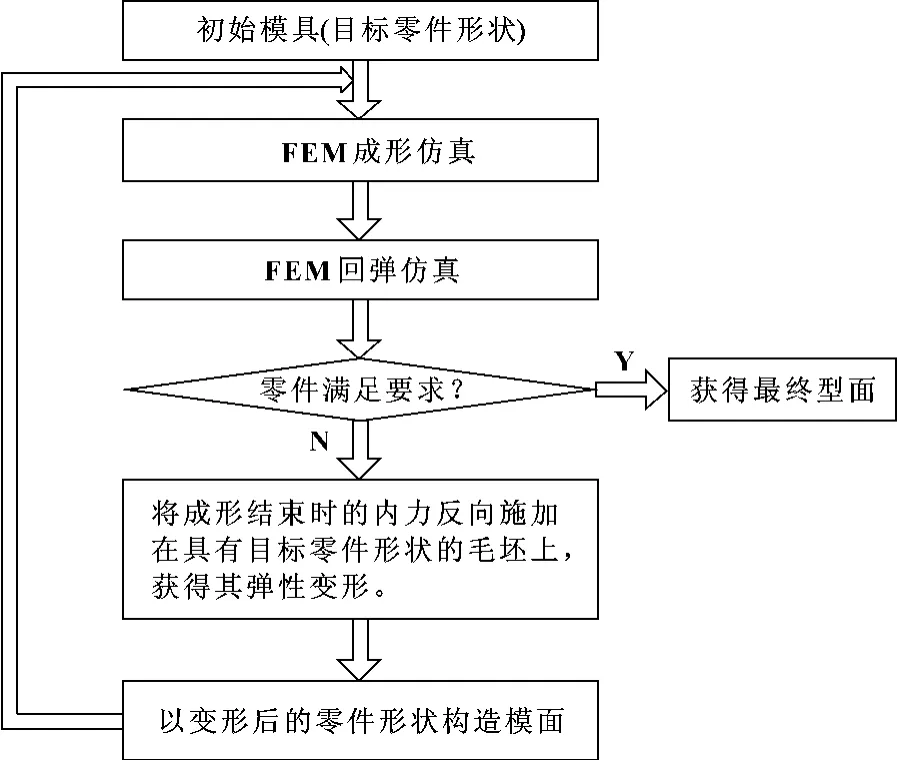
图2 FDM法的流程图

WU 等[36－38]验证了该方法的实用性并为首次成形后内力F 增加了个乘数因子α，α为回弹补偿因子，以αF 对零件进行有限元模拟仿真，当α=1时候，进行的是正常的回弹模拟，当α ＜0，板料成形后呈现的是反向的回弹。以后的每次迭代计算中α取不同的值，通过选择合适的α 进行板料回弹补偿可以使得板料的变形在误差允许的范围之内。

ANAGNOSTOU[39]对WU的方法进行了修改，对每次回弹补偿的补偿因子应用了另一种取值方法，提出了MSF法 (Modified Springforward Method)，图3介绍了该方法中α的取值方法。

FDM 等几种方法都是以力为研究手段，在解决回弹补偿问题上，操作位移也是一种重要的研究手段。GAN 等[40]提出了DA法 (Displacement Adjustment Method)，其思想是按照回弹反方向移动节点获得补偿型面。成形回弹计算后，将回弹结果和目标零件形状进行比较获得各节点的y坐标方向偏差值，然后将这些反向偏差值反向补偿到此次成形模面的对应节点上，构成新的模具型面，再以该补偿型面为基础按上述方法迭代计算，直到冲压件回弹仿真后的形状在误差范围之内。DA法的不足之处是只对某个方向进行补偿，补偿精度受到一定影响，而且在回弹计算的时候零件其他两个方向的数值将被改变，而且对于竖直的侧壁，DA法计算也不能收敛。另外该法形状补偿只能在坯料网格进行，而不能作用在其他的模具网格，也不能作用在CAD模型上[41]。

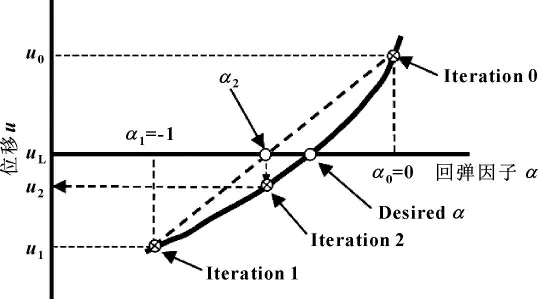
图3 MSF法α的取值方法

WEIHER 等[42]基于DA法提出了SDA法(Smooth Displacement Adjustment Method)。SDA法是将模具曲面(无论是离散的三角形网格、四边形网格，还是有控制点的CAD模型)用一个近似的连续且光顺的函数来表达，然后便可将回弹变形量应用于这些曲面进行迭代补偿。这样带来的好处是:(1)模具型面的光顺性得到保留;(2)模具的模面间距保持一致;(3)补偿时压边圈可以保持不变;(4)可以避免冲压负角的出现[43]。

SCO法[40](The Surface Controlled Overbending Method)也是由DA法演变而来，继承了DA法的基本原理，并且可以将形状修改直接用于CAD模型，然后CAD模型就可直接用于构建模具形状。但是SDA法和SCO法也存在其局限性，SDA法的逼近函数丢失了模型的局部细节，补偿效果不如DA，虽然可以使用高阶多项式，保留更多的细节，但是随着阶数的增加，该算法的不稳定性也随之增加。SCO法的控制曲面更适用于2D形状补偿，对于复杂的型面补偿，控制曲面的控制点要增加很多，这也会导致曲面匹配和回弹补偿的不稳定。

CHENG 等[44]总结了DA、FDM、MSF 等方法，结合几何修正和回弹计算，提出了一种加速的回弹补偿方法，继承了迭代法的基本思想，但是每次迭代开始所用的内力不是上一次成形结束阶段的内力，而是将此次成形回弹后的形状变形至理想零件形状所需要的内力。这个方法可以取得更快的收敛速度，但只是在2D 弯曲件的情况下得到验证，对于复杂的三维零件，收敛速度优越性还有待验证。

ANGGONO 等[45]将FDM法和DA法结合起来，在回弹补偿的首次迭代中应用DA法，之后如果回弹量在误差允许范围之内则停止;否则下面的迭代使用FDM法，直至满足要求。这种方法只是简单的组合，并没有带来补偿精度上的提高，但是结合了两者的优点，可以提高计算速度，因为DA法收敛速度快，首次迭代中使用可以尽快减少误差，之后误差较小刚好适用FDM法，因为FDM 收敛速度比较慢但比较稳健[40]。

聂昕等人[46]提出了SGD (Shape Global Deformation)算法并将其应用于回弹补偿分析中，进行补偿面的修改。SGD算法的基本原理是:基于最小能量原理，通过建立一个变形函数能够将一个整体进行变形，同时保持其原模型的连续性。龚志辉等[47]提出了基于仿真误差补偿模型的回弹补偿新方法。

YANG 等[48]以回弹补偿方向为研究角度，将补偿方法分为了RS法(冲压方向法)、RD法(连线补偿法)、RN法(法向补偿法)，分析了这3种方法的特点、适用情况与不足之处，提出了CC法(综合补偿法)。这种方法利用了2D 纯弯曲的几何关系并引入角度系数λ 来获得更准确的补偿方向。他们依据DA法位移补偿原理，在补偿方向上分别应用这4种方法(DA法本身属于RS法)，用V形和U形零件进行实验并验证了CC法的优越性。这种方法的理论构建与实验是建立在二维简单零件的基础之上，但是该方法是从一个新的角度来研究如何提高回弹补偿精度，取得了较好的补偿的效果。

上述回弹补偿方法的提出与验证都是从简单零件入手，但补偿的最终目的还是应用于实际生产。对于上述补偿方法在工业复杂零件上的应用，一些学者进行了实验研究，也取得了不错的回弹补偿效果。LINGBEEK 等[49]对NUMISHEET 2005benchmark #1 应用SDA法进行了回弹补偿，该零件形状十分复杂，但最终变形量减少了80%以上。LINGBEEK 等[50]以一个大众汽车翼子板为例，应用DA法进行回弹补偿，变形量减少了90%以上。尽管FEM技术解决回弹问题的精度已经得到了很大的提高，现在的精度和稳定性还不足以使该技术在工业中全面推广应用[43]。但是，随着FEM技术和回弹补偿方法研究的不断进步，数值模拟技术将逐步地应用于实际生产，成为解决回弹问题的关键手段。

3 基于FEM 回弹预测与补偿研究的发展方向

国际板料成形数值模拟会议(NUMISHEET)的标准考题体现了该领域的的研究热点，从1993年至今年在韩国召开的NUMISHEET2011，都涉及到回弹问题，并占据了比较大的比重，不难看出回弹问题研究的难度与热度及其重要性。越来越多的企业开始意识到回弹预测与补偿模拟技术的价值。根据目前发展状况可知，今后一段时期的几个研究发展方向包括:(1)继续提高精度。目前，众多国际著名的汽车公司在汽车覆盖件模具设计制造中，都要求在设计完成后必须经过计算机模拟检验，才能进行模具的制造。仅仅对成形过程来说，虽然板料成形FEM 模拟已达到了实用程度，但是作为回弹模拟的前提，其误差还会积累到回弹过程，成形精度还需进一步提高。回弹问题过程复杂，涉及的影响因素繁多，回弹模拟结果仍然不尽人意。应该更深入地探究零件和模具形状、拉延筋、压边力、材料模型、摩擦润滑条件、冲压设备等因素对成形结果与回弹性能的影响，发展与应用新的本构方程、屈服准则和摩擦模型，特别是对于某些新材料的材料模型。提高数值模拟的精度仍然是未来较长一段时期内回弹研究的重点。(2)采用新的研究手段。回弹问题十分复杂，具有非线性，涉及多学科知识、理论不完善、实验难等问题，目前的研究水平要用精确的数学表达形式来描述是不可能的。随着计算方法、计算机等技术的发展，应用一些新的研究方法也是研究回弹问题的有效策略。如FORCELLESE 等[51]和KAZAN 等[52]结合FEM与神经网络，FU 等[53]结合FEM 和遗传算法、BP 神经网络应用于回弹预测与控制，取得了一定的效果。(3)完善补偿算法。回弹补偿算法直接影响补偿效果，但现在的补偿算法在某些方面(比如补偿原理、收敛性、稳定性、计算效率、复杂零件适用性等)还存在一些不足，尤其是针对复杂模型的时候，模拟效果还不够理想，在今后仍需继续完善回弹与补偿算法，提高回弹模拟精度，进而研究控制回弹的更有效方法。(4)智能化和集成化。采用目前的技术处理回弹问题时效率仍然比较低，需花费较高的成本。随着技术的高速发展、竞争的日益激烈、客户需求的不断攀升，种种挑战和困难迫使企业需更快速地随需变革，如何用较少的资金、时间、人力去适应多变的市场需求，则成为现代制造企业应对挑战、赢得主动的关键。将人工智能、专家系统等智能技术应用于回弹控制技术，获取优化方案，并与其他技术集成起来、实现产品的CAD/CAE/CAM 一体化是也是FEM 回弹控制技术的重要发展方向。

4 结论

近年来，回弹预测与补偿问题逐渐成为了板料成形模拟领域的研究重点，作者首先从材料模型、单元类型、接触处理以及FEM算法等方面分析并论述了FEM 在回弹预测方面的发展现状;然后介绍了最近发展的几种回弹测评的方法，并对回弹补偿算法的研究历史和最新发展状况作了较全面的介绍;根据研究与发展的历史与现状，概括了该技术的未来的几个重点发展方向。文中的研究对回弹问题的研究具有一定的指导意义。随着FEM技术的发展、生产要求的提高以及越来越多的企业与研究者的不断深入探索，基于FEM的回弹预测与补偿技术将会得到更大的发展。

【1】钟志华，李光耀.薄板冲压成型过程的计算机仿真与应用[M].北京:北京理工大学出版社，1998:11－16.

【2】朱东波，孙琨，李涤尘，等.板料成形回弹问题研究新进展[J].塑性工程学报，2000，7(1):11－16.

【3】林忠钦.汽车覆盖件冲压成形仿真[M].北京:机械工业出版社，2004:22－24.

【4】BARLAT F，LIAN J.Plastic Behavior and Stretch Ability of Sheet Metals:Part I:A Yield Function for Orthotropic Sheets under Plane Stress Conditions[J].International Journal of Plasticity，1989，5:51－66.

【5】BARLAT F，LEGE Daniel J，BREM John C.A Six-component Yield Function for Anisotropic Materials[J].International Journal of Plasticity，1991，7:693－712.

【6】BARLAT F，BECKER R C，HAYASHIDA Y，et al.Yielding Description for Solution Strengthened Aluminum Alloys[J].International Journal of Plasticity，1997，13(4):385－401.

【7】BARLAT F，BREM J C，YOON J W，et al.Plane Stress Yield Function for Aluminum Alloy Sheets:Part 1:Theory[J].International Journal of Plasticity，2003，19:1297－1319.

【8】柳玉起，徐丹，许江平.改进的5参数Barlat-Lian 屈服准则[J].华中科技大学学报:自然科学版，2008，36(1):129－131.

【9】陈志英，董湘怀.各向异性GTN 损伤模型及其在板料成形中的应用[J].上海交通大学学报，2008，42(9):1414－1418.

【10】刘艳，谢值州，肖华，等.影响板料成形回弹数值模拟精度的因素分析[J].断崖装备与制造技术，2005，41(5):55－59.

【11】TAHERIZADEH Aboozar，GHAEI Abbas，GREEN Daniel E，et al.Finite Element Simulation of Springback for a Channel Draw Process with Drawbead Using Different Hardening Models[J].International Journal of Mechanical Sciences，2009，51(4):314－325.

【12】VLADIMIROV I N，PIETRYGA M P，REESE S.Prediction of Springback in Sheet Forming by a New Finite Strain Model with Nonlinear Kinematic and Isotropic Hardening[J].Journal of Materials Processing Technology，2008，209(8):4062－4075.

【13】张冬娟.板料冲压成形回弹理论及有限元数值模拟研[D].上海:上海交通大学，2007.

【14】李光耀，王琥，杨旭静，等.板料冲压成形工艺与模具设计制造中的若干前沿技术[J].机械工程学报，2010，46(10):31－39.

【15】BüCHTER Norbert，RAMM Ekkehard，ROEHL Deane.Three Dimensional Extension of Non-linear Shell Formulation Based on the Enhanced Assumed Strain Concept[J].International Journal for Numerical Methods in Engineering，1994，7:2551－2568.

【16】SANSOUR C.A Theory and Finite Element Formulation of Shells at Finite Deformation Involving Thickness Change[J].Archive of App-lied Mechanics，1995，65:194－216.

【17】PARISCH H.A Continuum-based Shell Theory for Nonlinear Applications[J].International Journal for Numerical Methods in Engineering，1995，38(11):1855－1883.

【18】HAUPTMANN R，SCHWEIZERHOF K.A Systematic Development of‘Solid-shell’Element Formulations for Linear and Nonlinear Analyses Employing Only Displacement Degrees of Freedom[J].International Journal for Numerical Methods in Engineering，1998，42(1):46－69.

【19】LI K P，CARDEN W P，WAGONER R H.Simulation of Springback[J].International Journal of Mechanical Sciences，2002，44:103－122.

【20】ALVES de SOUSA Ricardo J，CARDOSO Rui P R，FONTES VALENTE Robertt A，et al.A New One-point Quadrature Enhanced Assumed Strain(EAS)Solid-shell Element with Multiple Integration Points along Thickness:Part I:Geometrically Linear Applications[J].International Journal for Numerical Methods in Engineering，2006，67(7):160－188.

【21】许江平，柳玉起，杜亭，等.一种新的实体壳单元在板料成形中的应用[J].塑性工程学报，2009，16(2):48－52.

【22】吴勇国.板料成形过程数值模拟研究[D].武汉:华中理工大学，1995.

【23】MALONE James G，JOHNSON Nancy L.A Parallel Finite Element Contact/Impact Algorithm for Non-linear Explicit Transient Analysis:PartⅠ:the Search Algorithm and Contact Mechanics[J].International Journal for Numerical Methods in Engineering，1994，37(4):559－590.

【24】YANG D Y，YOON J W，YOO D J.Finite Element Simulation of Sheet Metal Forming by Using Non-parametric Tool Description with Automatically Refined Patches[C]//Proceeding of the Fourth ICTP，Beijing，China，1993:799－804.

【25】王晓林，周贤宾.板料成形数值模拟接触搜索模型的研究[J].塑性工程学报，2000，26(3):348－351.

【26】钟志华，李光耀.冲压成形CAE技术中接触摩擦计算的新方法[J].机械工程学报，2001，37(2):33－37.

【27】ZHONG Z H.Finite Element Procedures for Contact-impact Problems[M].New York:Oxford University Process，1993:256－330.

【28】WANG S P.Nonlinear Arc Contact and Friction Modeling in Dynamic Explicit Finite Element Analysis[OL].Numishe-et’96.

【29】陈中奎，施法中.板料冲压成形过程有限元分析中的接触搜索算法[J].塑性工程学报，2000，7(2):44－47.

【30】陈喜娣，蔡中义，李明哲.板材无压边多点成形中回弹的数值模拟[J].塑性工程学报，2003，10(5):9－13.

【31】邹付群，成思源，李苏洋，等.基于Geomagic Qualify软件的冲压件回弹检测[J].机械设计与研究，2010，26(2):79－81.

【32】龚志辉，钟志华.基于逆向工程技术实现汽车覆盖件回弹评测[J].湖南大学学报:自然科学版，2007，34(1):24－29.

【33】邵鹏飞，王秀喜，车玫.板料成形中的回弹计算和模具修正[J].机械强度，2001，23(2):187－189.

【34】WEBB R D，HARDT D E.A Transfer Function Description of Sheet Metal Forming for Process Control[J].Journal of Engineering for Industry，1991，113(1):44－52.

【35】KARAFILLIS A P，BOYCE M C.Tooling and Binder Design for Sheet Metal Forming Processes Compensation Springback Error[J].International Journal of Machine Tools and Manufacture，1996，36(4):503－526.

【36】WU L，DU C，ZHANG L.Iterative FEM Die Surface Design to Compensate for Springback in Sheet Metal Stampings[C]//Proceedings of NUMIFORM’95，New York，1995:637－641.

【37】WU L.Generate Tooling Mesh by FEM Virtual Forming Model for Springback Compensation in Die Surface Design of Sheet Metal Stamping[C]//Proceedings of the 1996 SAE International Congress ＆ Exposition，Detroit，1996:643－649.

【38】WU L.Tooling Mesh Generation Technique for Iterative FEM Die Aurface Design Algorithm to Compensate for Springback in Sheet Metal Stamping[J].Engineering Computations，1997，14(6/7):630－648.

【39】ANAGNOSTOU E L.Optimized Tooling Design Algorithm for Sheet Metal Forming over Reconfigurable Compliant Tooling[D].Stony Brook:State University of New York，2002.

【40】GAN Wei，WAGONER R H.Die Design Method for Sheet Springback[J].International Journal of Mechanical Sciences，2004，46(7):1097－1113.

【41】LINGBEEK R，HUéTINK J，OHNIMUS S，et al.The Development of a Finite Elements Based Springback Compensation Tool for Sheet Metal Products[J].Journal of Materials Processing Technology，2005，169(1):115－125.

【42】WEIHER J，RIETMAN B，KOSE K，et al.Controlling Springback with Compensation Strategies[C]//AIP Conference Proccedings，2004:1011－1015.

【43】MEINDERS T，BURCHITZ I A，BONTE M H A，et al.Numerical Product Design:Springback Prediction，Compensation and Optimization[J].International Journal of Machine Tools and Manufacture，2008，48(5):499－514.

【44】CHENG Hang Shawn，CAO Jian，XIA Z C.An Accelerated Springback Compensation Method[J].International Journal of Mechanical Sciences，2007，49(3):267－279.

【45】ANGGONO A D，SISWANTO W A，OMAR B.Combined Method of Spring-forward and Spring-back for Die Compensation Acceleration[C]//Modeling，Simulation and Applied Optimization(ICMSAO)，Kuala Lumpur，2011:1－6.

【46】聂昕，成艾国，申丹凤，等.型面修改的新算法SGD 及其在回弹补偿中的应用[J].中国机械工程，2008，19(24):2972－2976.

【47】龚志辉，李光耀，钟志华，等.基于仿真误差补偿模型的回弹补偿新方法[J].中国机械工程，2008，19(11):1358－1363.

【48】YANG X A，RUAN F.A Die Design Method for Springback Compensation Based on Displacement Adjustment[J].International Journal of Mechanical Sciences，2011，53(6):399－406.

【49】LINGBEEK R.A，HUETINK J，OHNIMUS S，et al.Iterative Springback Compensation of NUMISHEET Benchmark#1[C]//NUMISHEET 2005，6th International Conference and Workshop on Numerical Simulation of 3D Sheet Metal Forming Processes，Detroit，2005:328－333.

【50】LINGBEEK R，MEINDERS T，OHNIMUS S，et al.Springback Compensation:Fundamental Topics and Practical Application[C]//Ninth ES-AFORM Conference on Material Forming.Glasgow，U K，2006:403－406.

【51】FORCELLESE A，GABRIELLI F，RUFFINI R.Effect of the Training Set size on Springback Control by Neural Network in an Air Bending Process[J].Journal of Materials Processing Technology，1998，80/81:493－500.

【52】KAZAN R，FIRAT M，TIRYAKI A E.Prediction of Springbackin Wipe-bending Process of Sheet Metal Using Neural Network[J].Materials ＆ Design，2009，30:418－423.

【53】FU Z，MO J，CHEN L，et al.Using Genetic Algorithm Back Propagation Neural Network Prediction and Finiteelement Model Simulation to Optimize the Process of Multiple-step Incremental Air-bending Forming of Sheet Metal[J].Materials ＆ Design，2010，31:267－277.