磁流变阻尼器磁场响应时间分析和校正电路设计

杨哲，朱超，郑佳佳，王炅

(南京理工大学机械工程学院，江苏南京210094)

磁流变阻尼器作为一种半主动减振装置，具有结构简单、能耗低、提供阻尼力大等优点[1]，使其得到了广泛的应用。磁流变阻尼器的性能指标除了输出阻尼力大小、可调范围以外，磁流变阻尼器的响应时间是另一个重要指标，它直接决定着阻尼器的控制效果[2]。响应时间越短，越有利于实时控制，控制效果越好。尤其是在高冲击载荷下，作用过程迅速，通常只有几百毫秒，这对磁流变阻尼器实时控制系统快速响应提出了更加苛刻的要求，减少磁流变阻尼器的响应时间尤为重要。

到目前为止，对磁流变阻尼器响应时间的研究主要集中在响应时间的测量、影响响应时间因素的分析，已有的改进响应时间的研究也只限于磁路设计、更换电流源以及使用双向驱动电路等方面[3－4]。作者从控制工程的角度建立响应时间的传递函数模型，在此模型的基础上，设计了有超前相位的补偿传递函数，并据此设计了超前校正电路，类似的研究未见报导。

1 响应时间

磁流变阻尼器从感知扰动到产生控制力的过程所需要的时间为阻尼器的响应时间。由磁流变阻尼器的工作原理可知，磁流变阻尼器响应时间分为磁流变液材料的响应时间和电磁回路的响应时间两部分[5]。磁流变液装置的相容性和产生磁场的能力是影响磁流变液响应时间的两个主要因素[6]，在阻尼器结构设计完成后磁流变液的响应时间就基本确定，而电磁回路的响应时间与控制方法和电路硬件的设计有关，灵活性较大，所以这里主要考虑电磁回路的响应时间。

1.1 电流和磁场响应时间分析

影响电流和磁场响应的主要因素是电路中的电感和涡流。当控制电流变化时，由于以上两种因素对电流对磁场的迟滞作用，使电磁回路中的电流和磁场不能及时的发生变化，从而影响阻尼器的响应时间。

下面首先分析电流的响应时间。当忽略阻尼器铁芯中的涡流作用时，阻尼器的电磁回路可以简化为电阻和电感的串联模型，如图1所示。

图1 磁流变阻尼器的简化电磁模型

根据基尔霍夫定律，阻尼器两端的压降U(t)与所加的电流i(t)满足方程:

式中:U(t)是加在阻尼器上的电压;L是线圈的等效电感;R是阻尼器的等效电阻;i(t)是流过阻尼器的电流。

在阻尼器的工作过程中，控制电流的变化形式是不确定的，所以定义上述电路的响应时间如下:在零时刻，往电路两端加载一恒定的电压，电流从零变化到稳定值的95% 所用的时间。设加载的电压为U0时，由(1)式可得:

1.2 响应时间的传递函数

对式(2)进行拉普拉斯变换得:

经整理得:

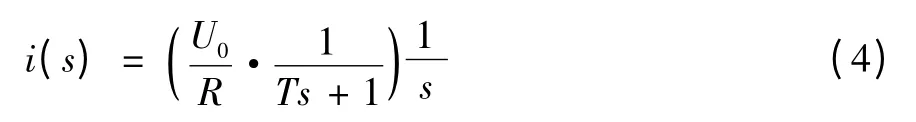
由此可以看出，阻尼器简化的电磁模型可以看成传递函数中的一阶惯性系统，电流在恒定电压下的响应可以看成一阶惯性系统对阶跃信号的响应。

文中设计的目的是:通过改变电路的传递函数来改善电流的响应时间。由于阻尼器设计完成之后，其传递函数是一定的，所以只能通过串联或者并联新的传递函数来改变电路的性能。常用的超前校正传递函数为:

其中:0 ＜α ＜1;T为超前传递函数的时间常数。超前校正传递函数有正相移，即在相位上超前于输入，所以能加速峰值的到来。但是，超前校正有增益损失，必须进行增益补偿。

2 超前校正电路的设计

2.1 校正电路的设计

为了得到超前校正传递函数，设计了超前校正电路，如图2所示。

图2 超前校正电路图

其中Xi(s)为输入，Xo(s)为输出，其传递函数为:

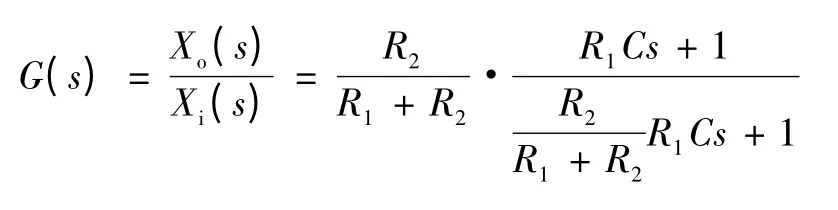
令:

2.2 确定传递函数和校正电路参数

为了验证磁流变阻尼器在恒定电压下电流和磁场的响应模式，进行了实验测试。选用的阻尼器为三级串联，电阻为5.8 Ω，由于电感不容易精确计算得出，所以通过实验来间接测量电感。另外，直接测阻尼器两端的电压信号容易出现干扰，因此，在电路中串联一个功率电阻，通过测量功率电阻两端的电压信号来观察电路中电流的变化，用高斯计的Monitor端口与示波器相连来记录阻尼器线圈上的磁场变化。由公式(2)可知，响应时间与电压大小无关，这一点在测试的时候也得到了证明。图3和图4分别是在线圈两端稳定电压为11.6 V时的阶跃电压信号下测得的电流和磁场随时间的上升曲线。

图3 电流(用电压表示)随时间的上升曲线

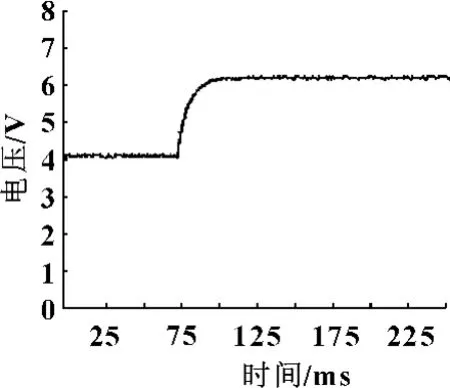
图4 磁场(用电压表示)随时间的上升曲线

图3和图4的横坐标是时间，图3中每格代表2.5 ms，图4中每格代表25 ms;纵坐标是电压，图3中每格代表2V，图4中每格代表1V。因为主要关注的是上升时间，为方便对比，用MATLAB 把两图画在一起时对两图的幅值归一化处理，如图5所示。

图5 电流和磁场响应时间对比

从图5可以清楚地看到，由于涡流的存在，使得磁场建立的时间远大于电流的响应时间。令式(4)中通过反复试凑，可以找到两条和实际测得的响应曲线符合较好的一阶惯性传递函数:

电流响应传递函数:

磁场响应传递函数:

由式(9)可得，磁场响应的时间常数是TM=0.006 5，由:

其中，LM是考虑涡流影响时磁路的等效电感。由于磁场的响应时间大于电流响应时间，所以磁场的响应时间便是阻尼器的电路的响应时间。在确定超前校正电路参数时就以式(9)为依据。因为一阶系统总是稳定的[8]，因此设计校正传递函数时，让式(5)分子与式(9)分母相等。即令:

令R1=3 Ω，由式(6)和式(7)可得:R2=1 Ω，C=2.17 mF。

3 仿真

在MATLAB 中对增加传递函数前后磁场响应时间进行仿真，其仿真模型如图6所示。

图6 磁场响应时间仿真模型

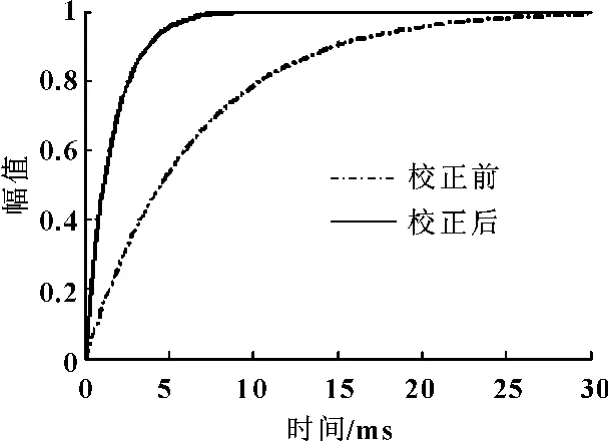
图7 磁场响应时间仿真结果

可以看出，校正后磁场响应时间要快得多，只需5 ms 就可以达到稳定幅值的95%，而不加校正的话则需要20 ms。

在PROTEUS 中分别建立未加校正电路和增加校正电路的磁流变阻尼器磁场响应电路来仿真校正效果，电路图如图8和图9所示，仿真结果见图10。

图8 阻尼器磁场响应等效电路图

图9 校正后的磁场响应等效电路图

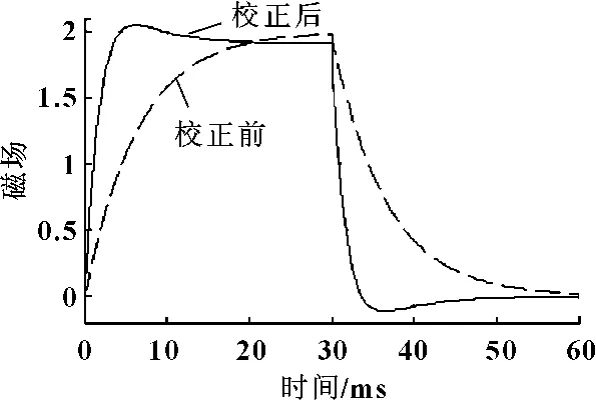
图10 磁场在阶跃上升和下降电压下的响应曲线

其中图8中加载的电压幅值为11.6 V，为使响应信号有相同的幅值，图9中加载的电压幅值是图8中的4倍。由仿真结果图10可以看出，校正前磁场响应时间在20 ms 左右，校正后响应时间缩短至5 ms左右，这与在MATLAB 中的仿真结果是一致的。同样可以看出，在阶跃下降信号时，校正后电路的磁场响应也比校正前迅速得多。

4 结论

首先从阻尼器的简化模型推导出了阻尼器电流响应的传递函数，然后通过实验，拟合出了磁场响应的传递函数。并利用超前校正传递函数理论，设计了超前校正电路，在MATLAB 和PROTEUS 中对设计的电路进行了仿真，结果表明所设计的电路能够有效缩短磁场的响应时间。但是，电路中提供的电压值也必须升高。在作用时间很短，对响应时间要求苛刻的快速、高冲击减振过程中，上述电路能充分发挥自身的优势。

【1】CESMECI Sevki，ENGIN Tahsin.Modeling and Testing of a Field-controllable Magnetorheological Fluid Damper[J].International Journal of Mechanical Sciences，2010，52(8):1036－1046.

【2】YANG G，SPENCER Jr B F，CARLSON J D，et al.Largescale MR Fluid Dampers:Modeling and Dynamic Performance Considerations[J].Engineering Structures，2002，24(3):309－323.

【3】黄曦，余淼，陈爱军，等.磁流变阻尼器动态响应及其影响因素分析[J].功能材料，2006，37(5):808－813.

【4】YANG G.Large Scale Magneto-rheological Fluid Damper for Vibration Mitigation Modeling Testing and Control[D].Department of Civil Engineering and Geological Sciences，Notre Dame，Indiana，2001.

【5】周玉丰，吴龙.磁流变阻尼器响应时间分析研究[J].重型机械科技，2006(2):10－13.

【6】汪建晓，孟光.磁流变液研究进展[J].航空学报.2002，23(1):6－12.

【7】郭鹏飞，关新春，欧进萍.磁流变液阻尼器响应时间的试验研究及其动态磁场有限元分析[J].振动与冲击，2009，28(6):1－4.

【8】董景新，赵长德，熊沈蜀，等.控制工程基础[M].北京:清华大学出版社，2003.