基于PSO搜索潜在滑裂面非极限状态土压力计算*
2013-03-19陈昌富肖重阳唐仁华
陈昌富,肖重阳,唐仁华
(湖南大学岩土工程研究所,湖南长沙 410082)
作用于刚性挡土墙上的土压力通常采用经典的朗肯或库仑土压力理论进行计算,但其计算的土压力与实测结果间往往会存在较大差异已是岩土工程界的共识.这两种理论只能求得极限状态的土压力,而在许多实际情况下,刚性挡土墙的位移量非常小,土压力处于极限土压力与静止土压力之间.为了更准确地进行挡土墙设计,有必要对非极限状态时的土压力计算进行研究.
Bang[1]认为土体从静止状态到极限状态是一个渐变的过程,提出了中间主动状态的概念,指出土压力计算应同时考虑墙体变位模式和位移的大小.Fang,Ishibashi[2]对不同变位模式下的土压力进行了模型试验研究,试验表明挡土墙土压力受墙体变位模式和位移大小的影响很大.Matsuzawa[3]等对不同变位模式下的挡土墙主动土压力进行了理论分析.蒋波等[4]改进了极限平衡理论,用于非极限状态主动土压力的研究,得到了平动变位模型下非极限状态主动土压力.徐日庆等[5]分析了最不利情况下墙后土楔的受力情况,得到考虑位移效应的非极限状态土压力计算公式.张永兴等[6]分析墙后填土微分单元体,得到了墙背竖直、填土面水平的非极限土压力理论公式.
已有的非极限状态土压力计算将滑裂面视为直线,而实际滑裂面为曲线.因此,本文对其作如下改进:1)将滑裂面视为一任意曲线,改进水平层分析法[7],对平动模式下墙后填土进行分析,推导非极限状态主动方向土压力分布、合力大小及作用点的计算公式.2)引入粒子群优化算法[8]对潜在滑裂面进行搜索从而获得非极限主动方向土压力最优解,并进行实例分析以及参数分析.
1 公式推导
1.1 非极限状态下摩擦角
由土体渐进破坏机理可知,当墙后土体处于非极限状态时,只有部分土体进入极限状态,假定非极限状态时土体内存在一潜在滑裂面,并假定在该潜在滑裂面上土体的抗剪强度部分、均匀地发挥,以此替代不便于计算的滑裂面上土体抗剪强度不均匀发挥,非极限状态下墙后填土的内摩擦角和墙土摩擦角分别用φm,δm表示,龚慈[9]根据Matsuzawa[3]和Sherif等[10]试验数据进行回归分析,得到以下公式:其中φ,δ为极限状态下的内摩擦角和墙土摩擦角;φ0,δ0分别为初始内摩擦角和墙土摩擦角;η=S/Sc为挡土墙实际位移与极限位移之比.

位移之比0≤η=S/Sc≤1.当η=0时,实际位移S=0,为静止状态;当η=1时,实际位移S=Sc为极限状态;当0<η<1时为非极限状态.Sherif等[10]基于试验数据提出了计算砂土所需Sc的经验公式:Sc=H(7.0-0.13φ)10-4.
对于δ的取值Matsuzawa和Hazarika[3]建议采用2φ/3,所得的挡土墙主动土压力系数与模型试验实测值最为接近.δ0如果没有给出确切的值,一般取δ0=φ/2.
土体初始内摩擦角φ0为静止状态时土体的内摩擦角,对于正常固结土体,若不考虑初始状态时墙土摩擦角δ0的影响,则

式中K0为静止侧土压力系数,K0=1-sinφ′,φ′为土体的有效内摩擦角.如果考虑δ0的影响则可采用改进的库伦公式:

由以上公式可以看出,非极限状态土压力的求解思路就是通过位移比η来控制内摩擦角和墙土摩擦角φm,δm的变化,从而得出挡土墙位移过程中土压力的变化情况.
1.2 模型的建立和公式推导
如图1所示,假定挡土墙在位移过程中形成的潜在破裂面为一通过墙踵的任意曲面,墙后填土为均质砂土.

图1 挡土墙计算模型Fig.1 Calculation model of retaining wall
挡土墙墙高为H,将墙后填土均匀地离散为n份,每个薄层微元高为h.以墙踵O点为原点(x1=0,y1=0),建立直角坐标系,第i个薄层微元右下角点坐标为(xi,yi),第i个薄层微元潜在滑裂面与水平面倾角为θi.
根据图1,图2可以得到如下递推关系:

式中Wi为薄层微元所受重力,γ为墙后填土重度.

图2 薄层微元受力分析Fig.2 Thin-layer element analysis
薄层单元的受力情况如图2所示(平动模式下薄层微元间水平剪力很小,忽略不计),由薄层单元水平方向力的平衡可得:

式中Pi为墙背反力,Ri为滑裂面反力.
由薄层单元竖直方向力的平衡可得:
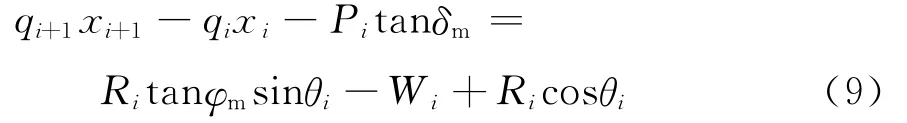
式中qi,qi+1为相邻薄层微元之间作用力.
对微元体滑裂面中点取力矩平衡可得:
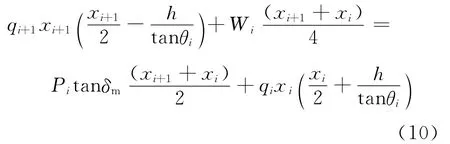
联立式(8)~式(10)可得:


将qn+1(考虑超载时qn+1=q0,不考虑超载时qn+1=0)代入式(11)中,通过递推可以将所有qi求出,然后将qi代入式(12)得出所有Pi.则土压力强度为:

土压力合力计算公式为:

土压力合力作用点计算公式为:

以上土压力计算公式包含未知变量θ1,θ2,…,θn,不能直接求解出来.本文和库仑土压力求解思路一样,找到一组[θ1,θ2,…,θn]使得非极限状态土压力Eam最大,此时[θ1,θ2,…,θn]对应破裂面为最危险破裂面.由于变量较多,用智能优化方法进行求解比较适合.
2 PSO搜索滑裂面
非极限状态主动土压力计算可归结为如下优化模型:

式中X为优化设计变量;f(X)为目标函数,计算土压力时f(X)=Eam;g(X)为约束条件,此处根据保凸性要求θ1≤θ2≤…≤θn.
式(18)是一个含有复杂的目标函数和约束条件的非线性优化问题,本文采用适用性强且具有良好的全局搜索能力的粒子群算法[11](PSO)求解.
在PSO算法中,每个粒子都具有3个参数:位置矢量X,代表目标函数中自变量的值;速度矢量V,代表粒子飞翔的力向和距离,用来引导粒子不断朝着更好的解空间改变当前位置;适应度fitness=-f(X)=Eam,由被优化的目标函数决定,目标函数值越小,则适应度越好.在每一次迭代中,粒子通过跟踪两个最优解来更新自己,一是粒子本身所找到的最优解,另一个是整个种群目前所找到的最优解.
基于以上原理和模型,非极限状态土压力粒子群优化算法计算步骤如下:
1)设定粒子群数目为80,即i∈[1,80].对每个粒子的当前位置矢量Xi=[xi,1,xi,2,…,xi,n]和速度矢量Vi=[vi,1,vi,2,…,vi,n]在变量范围内随机赋予初始值.
2)根据每个粒子当前的Xi计算其适应度.若g(Xi)成立,则fitness(i)=f(Xi);否则,将一个远大于正常土压值的大数赋给适应度函数作为此粒子的适应值以使其受到惩罚,例如fitness(i)=10 000.
3)将各微粒的位置和适应值存储在各微粒的个体最好位置pbest中,将所有pbest中适应值最优个体的位置和适应值存储于群体最好位置gbest中.
4)按式(19)和(20)更新每个微粒的速度和位置:

式中t为迭代的步数;pi为个体最优适应值对应的[xi,1,xi,2,…,xi,n]值,即第i个粒子最优适应值对应的[θ1,θ2,…,θn]值;pg为群体最优适应值对应的[θ1,θ2,…,θn]值;w为惯性权重因子,文中取w=0.5;c1,c2为正的学习因子,文中取c1=c2=2;r1,r2为[0,1]范围内的均匀随机数.
5)对每个微粒,将其适应值与其经历过的最好适应值比较,如果较好,则将其对应的位置作为当前的最好位置,然后比较当前所有pbest和gbest的值,更新gbest.
6)将整个粒子群按适应值排序,用群体中最好的一半的粒子速度和位置替换掉最差的一半的位置和速度,保持pbest和gbest不变.
7)设定最大迭代次数,达到迭代次数后则输出结果,即土压力最大时的θ1,θ2,…,θn值以及非极限状态土压力Eam大小.
3 实例分析
采用Fang,Ishibashi(1986)[2]的模型试验实测数据与采用本文提出公式的计算结果进行比较,如图3所示.

图3 土压力分布计算值与实验值对比Fig.3 Comparison of earth pressure distribution between calculated results and experimental results
该试验填土采用风干砂土,其性质为γ=15.4 kN/m3,φ=34°,墙高H=1.04m.由图可以看出,计算值与实验值的大小及变化趋势基本是一致的.墙底附近计算值与实测值存在偏差,这是由于本文的计算方法是由库仑土压力理论发展而来,而库仑土压力理论本身存在计算墙下部土压力与实测有差距的缺陷.
4 参数分析
为了探讨φ和位移比η对非极限状态土压力分布、土压力合力大小、土压力合力作用点高度以及潜在破裂面的影响,选取一高4.6m、墙后填土γ=19.2kN/m3的挡土墙进行参数分析.
如图4,墙后填土φ=30°时土压力强度随位移比η变化的情况.由图可以看出在平动模式下土压力的分布为一条非线性的曲线,这与FANG的实验观测是一致的[12].同时,随着η值的变大,土压力强度p是逐渐减少的,非极限土压力处于静止土压力与极限土压力之间.
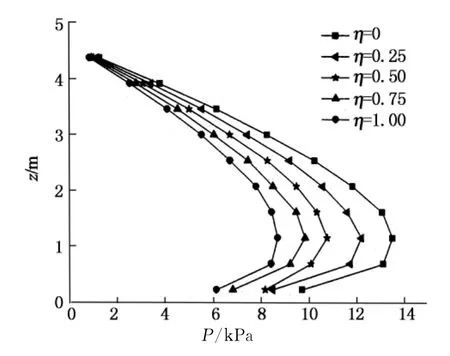
图4 位移比η对土压力分布的影响Fig.4 Distribution of earth pressure with different value ofη
图5为土压力合力随φ和η的变化而变化的关系图.由图可以看出随着η的增大,土压力合力逐渐减小,随着φ的增大也是呈减少趋势的,而且随着φ的增大土压力合力增大的趋势逐渐减弱.
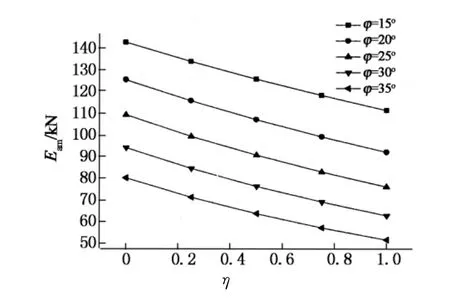
图5 φ和位移比η对土压力合力的影响Fig.5 Effect ofηandφon resultant earth pressure
表1为不同φ和η情况下土压力合力作用点的位置.由表可以看出非极限状态主动土压力合力作用点高度点介于0.36~0.38之间,都在墙高的1/3以上,这与FANG的模型试验结果相符[12].作用点位置随着φ和η的变化无特定变化规律.
图6与图7为φ和η取不同值时的破裂面和潜在破裂面形状,可以看出,挡土墙后填土破裂面不是通常方法假定的平面,而为一曲面,且曲率在底部较大.随着φ的增大,破裂面越靠近墙体,滑动土体越小,趋势与库仑公式计算结果一致.随着η的不断增大,潜在破裂面也不断靠近墙体.

图6 位移比η=1时不同φ对应的破裂面Fig.6 Slip surface with differentφwhenη=1
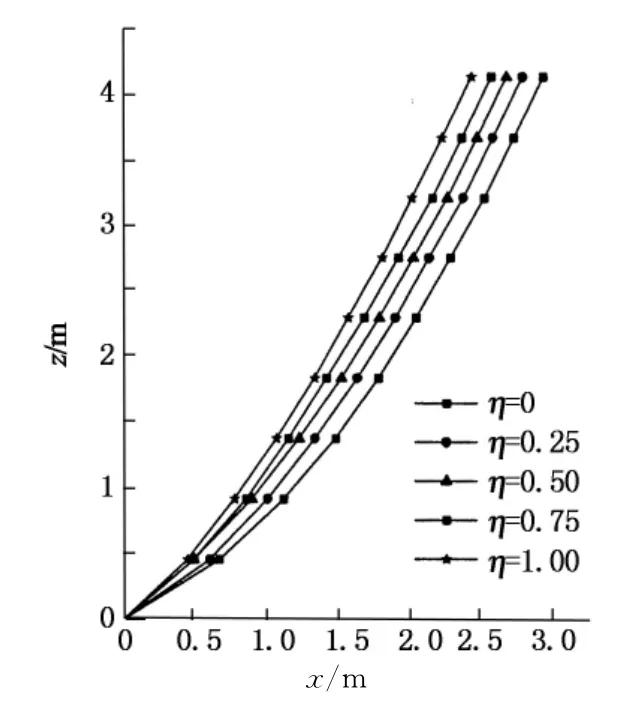
图7 φ=30°时不同位移比η对应的潜在破裂面Fig.7 Slip surface with differentηwhenφ=30°
5 结 论
本文改进了水平层分析法,假定墙后填土潜在滑裂面为一任意曲线.根据摩擦角随位移变化关系,对平动模式下墙后填土进行分析,推导出非极限状态下主动方向土压力分布、合力大小及作用点的理论公式.并且引入PSO优化算法对潜在滑裂面进行搜索,从而获得非极限状态土压力的最优解.
分析了φ,η对计算结果的影响.随着η值的变大,土压力强度分布P逐渐减少;非极限状态土压力合力随着φ和η的增大而减小;土压力合力作用点介于墙高的0.36~0.38之间,都在墙高的1/3以上;搜索出的潜在裂面为一曲线滑裂面,随着φ和η的增大,潜在滑裂面越靠近墙体,滑动体越小.
本文提出的理论计算方法得出的结果与试验数据的大小及变化趋势基本是一致的,对实际工程有参考应用价值.
[1] BANG S.Active earth pressure behind retaining walls[J].Journal of Geotechnical Engineering,1985,111(3):407-412.
[2] FANG Y S,ISHIBASHI I.Static earth pressure with various wall movements[J].Journal of Geotechnical Engineering,1986,112(3):317-333.
[3] MATSUZAWA H,HAZARIKA H.Analyses of active earth pressure against rigid retaining walls subjected to different modes of movement[J].Soils and Foundations,1996,36(3):51-65.
[4] 蒋波,应宏伟,谢康和,等.平动模式下挡土墙非极限状态主动土压力计算[J].中国公路学报,2005,18(2):24-27.JIANG Bo,YING Hong-wei,XIE Kang-he,et al.Computation of active earth pressure under non-limit state for retaining wall with mode of translation[J].China Journal of Highway and Transport,2005,18(2):24-27.(In Chinese)
[5] 徐日庆,龚慈,魏纲.考虑平动位移效应的刚性挡土墙土压力理论[J].浙江大学学报,2005,39(1):120-122.XU Ri-qing,GONG Ci,WEI Gang.Preliminary study of active earth pressure under non-limit state[J].Journal of Zhejiang University,2005,39(1):120-122.(In Chinese)
[6] 张永兴,陈林.挡土墙非极限状态主动土压力分布[J].土木工程学报,2011,4(4):113-118.ZHANG Yong-xing,CHEN Lin.Active earth pressure on retaining walls in non-limit state[J].China Civil Engineering Journal,2011,4(4):113-118.(In Chinese)
[7] 张军,王贻荪.确定挡土墙主动土压力分布的薄层分析法[J].湖南大学学报:自然科学版,1998,25(5):147-153.ZHANG Jun,WANG Yi-sun.Determination of active earth pressure distribution against retaining wall by thin layer method[J].Journal of Hunan University:Natural Science,1998,25(5):147-153.(In Chinese)
[8] KENNEDY J,EBERHART R C.Particle swarm optimization[C]//Proceeding of the 1995IEEE International Conference on Neural Network.Perth,Australia,1995:1942-1948.
[9] 龚慈.不同位移模式下刚性挡土墙土压力计算方法研究[D].杭州:浙江大学建筑与土木工程学院,2005.GONG Ci.Earth pressure against rigid retaining wall of different movement modes[D].Hangzhou:College of Civil Engineering and Architecture,Zhejiang University,2005.(In Chinese)
[10]SHERIF M M,ISHIBASHI I,LEE C D.Earth pressure against rigid retaining wall[J].Journal of Geotechnical Engineering,1982,108(5):679-695.
[11]龚纯,王正林.精通Matlab最优化计算[M].北京:电子工业出版社,2009.GONG Chun,WANG Zheng-lin.Proficient in the optimization based on matlab[M].Beijing:Publishing House of Electronics Industry,2009.(In Chinese)
[12]FANG Y S,CHENG F P,CHEN R C,et al.Earth pressures under general wall movements[J].Geotechnical Engineering,1993,24(2):113-131.
