负热膨胀材料在机床热误差补偿中的应用

魏效玲，陈稚文，王杰华

(河北工程大学机电学院，河北 邯郸056038)

材料的热胀性一直是影响工件加工精度不可避免的问题，根据英国佩克勒尼克教授和日本垣野义昭教授的研究表明，热变形误差是数控机床的最大误差源，约占总误差的 40% －70%［1－2］。负热膨胀材料具有与普通材料相异的冷涨热缩性，其体积在可接受的温度区间内随温度的升高而减小、随温度的降低而增大，而且膨胀系数可以叠加，理论上能够配制任意数值膨胀系数的材料。负热膨胀材料迅速发展，近年发现的锰氮化合物Mn3AN(A代表Zn，Ga，Cu)及其衍生化合物具有优秀的负热膨胀性能，其中 Mn3(Ga0.7Ge0.3)(N0.88C0.12)在197 K至319 K温区的线性膨胀系数可到－ 18 × 10－6K－1，Mn3(Ga0.5Ge0.4Mn0.1)N 在 316 K至386 K温区的线性膨胀系数可到－25×10－6K－1。这类材料导热性能优良，机械强度高，利用其负热膨胀的特性来减少机床热误差是一种新途径。

1 负热膨胀材料简介

依据负膨胀的机理不同，负热膨胀材料分为相结构转变类、桥氧原子横向热振动类、多面体摆动耦合类、固体内压转变类、相界面弯曲类、阳离子迁移类等;依据变形方向，分为各向同性材料和各向异性材料［3］。在应用负热膨胀材料时，影响使用性能的主要方面是热变形方向。各向异性是指材料晶格的不同方向具有不同的膨胀性质，各方向的膨胀量不一致或膨胀方向相反，材料会产生内应力，裂纹，降低机械强度，而且用其配置复合膨胀材料较为复杂，因此各向异性负热膨胀材料的应用受到很大限制。各向同性材料晶格的各方向热膨胀系数几乎相同，热变形方向一致，克服了各向异性材料的缺点，物理性能出色，成为负热膨胀材料的一个主要研究种类。

评价负热膨胀材料性能最重要的参数是热膨胀系数。热膨胀系数是指物质在热胀冷缩效应作用之下，几何特性(或尺寸)随着温度的变化而发生变化的规律性系数。实际应用中，有两种主要的热膨胀系数，分別是:

式中L－材料线性长度(mm);T－温度(℃);V－材料体积(m3)。

研究固体材料一般使用线性热膨胀系数，体积热膨胀系数通常用来衡量液体。各向同性钨酸盐负热膨胀材料的α值平均为－9×10－6K－1，各向异性钨酸盐与磷酸盐的负热膨胀材料α值平均约为 －4 ×10－6K－1，总体性能不理想。

2 热误差补偿技术

热误差的补偿方法主要有温度控制法、误差预防法、误差补偿法，常用的是误差补偿法。在研究热误差补偿方法时，学者们通常将机床－工件与刀具系统分开讨论，机床－工件系统一般在空机工况下研究，刀具系统则为单纯受热情况，刀具温度分布如图1所示。联立二者会使情况复杂，且测量工况中的参数存在难度。分析机床－工件系统首先是测量机床温度，在床体、主轴等重要受热部位布置较多温度采集点;继而采用神经网络、多元线性回归、灰关联、贝叶斯网络等数学方法去除噪点，辨识关键温度采样点，建立热误差模型，通常为轴向与径向的位置变化量与关键点温度之间的关系，即得到误差预测;最后通过采集工况参数、软件分析、硬件反应的过程对实际加工加以补偿。刀具系统同样是从热变形出发，通过热耦合理论等，由变形公式，判断刀具接触面的误差变化，加以补偿。热误差补偿的实质是依据经验、模型、公式，将实时温度作为唯一变量，预测地获得误差，由补偿机构控制刀具等走位进行补偿。这类方法虽然有很多新技术在完善，但还存在几个主要缺点:(1)系统有延迟性，反应往往落后实时补偿点;(2)额外的补偿系统使机床结构变得复杂;(3)系统可靠性低，一个环节失效将导致整个补偿过程失灵;(4)受环境影响大，鲁棒性差。基于上述缺陷，需要新的补偿方法对机床热误差进行补偿。

3 负热膨胀材料与热误差补偿

工件和传统刀具的热变形均表现为体积正膨胀，以车削为例，工件径向尺寸的增加(包括机床热变形对其的影响)与刀具轴向尺寸的增加共同导致过多的工件材料被切削，产生误差(如图2所示)。既然这是产生热误差的根本原因，在被动补偿热误差的方法外，使用负热膨胀材料作为刀具材料，利用其在受热时体积减小的特性，弥补工件热变形增量，理论上可以有效减小热误差(如图3所示)。机床体影响工件热变形的研究成果较多，刀具的热变形可以由有限元等方法获得，同时变形的来源是热传导(即温度变化)，热变形量受材料性质(导热系数、剪应变、热容量等)、切削用量(切削速度、进给量、切削深度)、刀具角度及工作环境所影响，若只研究一个变量，可以近似为线性函数，那么联立讨论工件和负热膨胀刀具是可行的。

在影响温度变化的因素中，刀具角度和工作环境的作用较小，切削用量对工件和刀具的影响效果大致相当。不同材料所具有的性质对温度变化的影响很大，但是温度对热变形的影响宏观地表现为热膨胀系数，在研究使用负热膨胀材料补偿热误差时可以主要讨论热膨胀系数的因素。(刀具的热变形量公式为式(3)［4］)

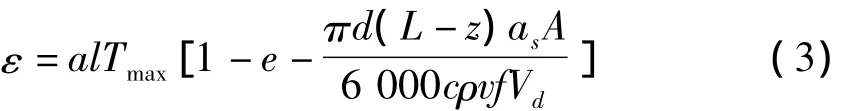
式中a－材料线性膨胀系数(1/℃);l－刀体悬伸部分长(mm);Tmax－热平衡时刀具最大平均温升(℃);L－车刀伸长量(mm);z－车刀与工件接触深度(mm);as－材料表面散热系数(W/(h m2℃));A－车刀散热表面面积(m2);Vd－车刀的体积(m3);ρ－车刀的密度(kg/m3);c－车刀的比热(J/kg℃);v－切削速度(m/min)。

相同尺寸、材质的工件，在相同工况下的热变形是一致的，这是误差补偿的前提。由式(3)可以看出，规定工况及车刀的物理几何参数后，刀具变形量变化与材料膨胀系数呈线性变化。利用传统温度检测的热误差模型，判断同一工况下的工件变形量，与刀具负热变形量联立，可以获得不同工况下负热膨胀材料对热误差的影响规律，进而选择最优解。

4 结束语

通过计算工作参数、刀具材料、误差量，建立工件材料－工况－负热膨胀材料刀具的数据库，针对某一种工况的工件，使用相对应的负热膨胀系数的刀具加以补偿热误差。该方法迅速快捷，刀具尺寸与工件的几何尺寸同步变化，能够即时补偿;系统简单，只需采用新刀具材料，不需复杂结构，为热误差补偿提供一种新方法。

［1］PEKLENICJ.Untersuchung der genauigkeritsfragen in der automatisierten fertigung［J］.Westdeutscherverlag，1967(2):19－24.

［2］垣野义昭.机床热变形对加工精度的影响［J］.机械与工具，1997(10):1841－1844.

［3］谭强强.复合氧化物材料的负热膨胀机理［J］.耐火材料，2001，35(5)296－298.

［4］李静，王占礼，王伟冰.车削加工仿真中刀具热变形对工件加工精度的影响［J］.工具技术，2009，43(6)，67－69.

［5］石东平，张维纪，程耀东.有限元法计算金属切削刀具温度场［J］.浙江大学学报，1990，3(24):411－419.

［6］陈锡渠，彭晓南.金属切削原理与刀具［M］.北京:中国林业出版社，2006.