基于自适应细菌觅食算法的灰度图像增强方法

翟自勇，赵卫国，王欢

(河北工程大学技术中心，河北 邯郸056038)

在图像的生成、传输和变换过程中，由于多种外在或者内在因素的影响，往往使图像与原始图像之间产生某些差异，很多情况下会使原有图像降质。降质后的图像使得从图像中获取各种信息造成某种困难和不便［1］。因此，有必要对降质的图像进行适当的处理以提高图像的质量。图象增强技术就是为了改善图像的视觉效果，通过某种方法或者技术手段将原来不清楚的图像变得更清晰或把感兴趣的某些特征体现出来。Tubbs［2－4］针对灰度图像的空间域增强算法提出了一种能完全覆盖图像增强典型变换函数类型的非完全Beta函数，但是确定Beta函数参数仍是一个比较复杂的问题。因此，去寻找一种可行的方法依据图像灰度级性质自动调节的图像增强算法是非常必要的［5］。

细菌觅食优化算法是近年来提出的较为新颖的智能优化算法，该算法和其他智能优化算法如遗传算法、蚁群算法等一样，是一种随机搜索算法，它模拟大肠杆菌的觅食行为，具有很好的搜索能力。本文提出了一种具有自适应能力的细菌觅食优化算法，并利用能完全覆盖图像增强变换函数类型的非完全Beta函数，用粒子群算法实现了选择非完全Beta函数的最佳参数，从而获得一条最佳的灰度变换曲线，以此达到了灰度图像的自适应增强。

1 细菌觅食算法

细菌觅食算法［6］是一种仿生随机搜索的优化算法。对于细菌觅食系统来讲，共有四个最基本的觅食原则，它们分别是:游动和翻转、趋向性、复制和迁移。

1.1 游动和翻转

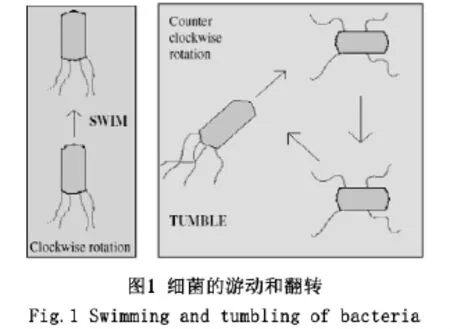
与细菌底部相连的鞭毛具有左手螺旋特点，从鞭毛的末端向细菌看去，细菌的底部是按照逆时针旋转，这样它会对细菌产生一个反推力，这种运动模型被称为游动。但是如果鞭毛顺时针旋转，那么会对细菌产生一个拉力，因此每个鞭毛相对于其它鞭毛做相对运动，这样都会导致细菌做翻转运动。翻转运动表示对下一步游动进行方向上的调节，他们总是向着有食物的地方游动，往往遇到不利的环境就进行翻转进行方向调节。图1描述了细菌的游动和翻转的两种运动［7］。

细菌每移动到新的位置，将根据式(1)计算个体间感应值［8］

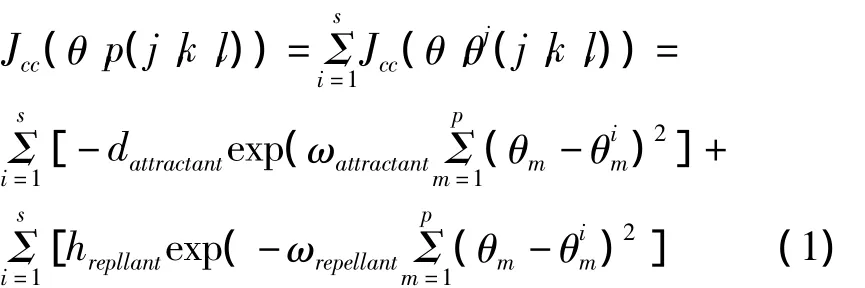
式中Jcc(θ，p(j，k，l))－ 在第j次趋向操作、第k次复制和第l次迁移操作时，第i个细菌的个体间感应值之和;Jcc(θ，θj(j，k，l))－ 每两个细菌之间的群体感应值;dattractant－吸引因子的数量ωattractant－吸引因子的数量和释放速率;hrepllant和ωrepellant－排斥因子的数量和释放速率;S－细菌种群规模;p－细菌搜索环境的维数;θi m－第i个细菌所在位置的第m维。

1.2 趋向性

细菌的整个生命周期就是在做游动和翻转运动，其目的是寻找食物并避开不利物质和环境，我们称这种现象为趋向性行为，这种行为可用式(2)描述

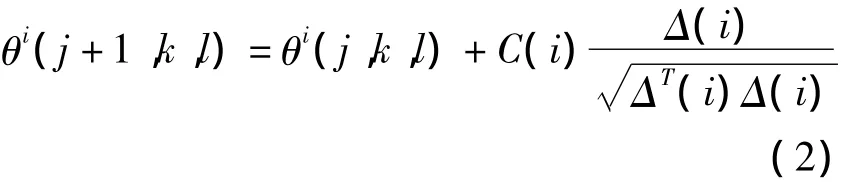
式中Δ(i)－细菌随机性翻转中生成的任意方向向量，范围为进行方向调整后选定的单位向量，细菌的游动操作可视为对可行解的搜索。

1.3 复制

经过一段时间的食物搜索后，部分没有找到足够食物的细菌被自然淘汰掉，为维持种群规模，一部分觅食能力强的细菌会进行自身复制，替换掉被淘汰的细菌，在细菌觅食优化算法中模拟这种现象称为复制行为。设群体的规模为S，淘汰掉的细菌个数为Sr=S/2，首先根据细菌的适应度进行排序，把排在后面的Sr个细菌淘汰掉，然后对剩余的Sr个细菌进行复制，这样保证了群体规模的稳定性。

1.4 迁移

细菌个体的生活区域可能会因各种因素如温度和食物多少等而发生变化，从而会导致生活在这个局部区域的细菌种群集体死亡或者迁移到另外一个新的局部区域，在细菌觅食系统中模拟这种现象称为迁移行为［9］。迁移行为以一定概率发生，如果种群中的某个细菌满足迁移发生的概率，则这个细菌个体灭亡，并随机地生成一个新个体，迁移生成的这个新个体可能更靠近全局最优解。

2 基于细菌觅食的自适应图像增强算法

2.1 图像增强的非完全Beta函数

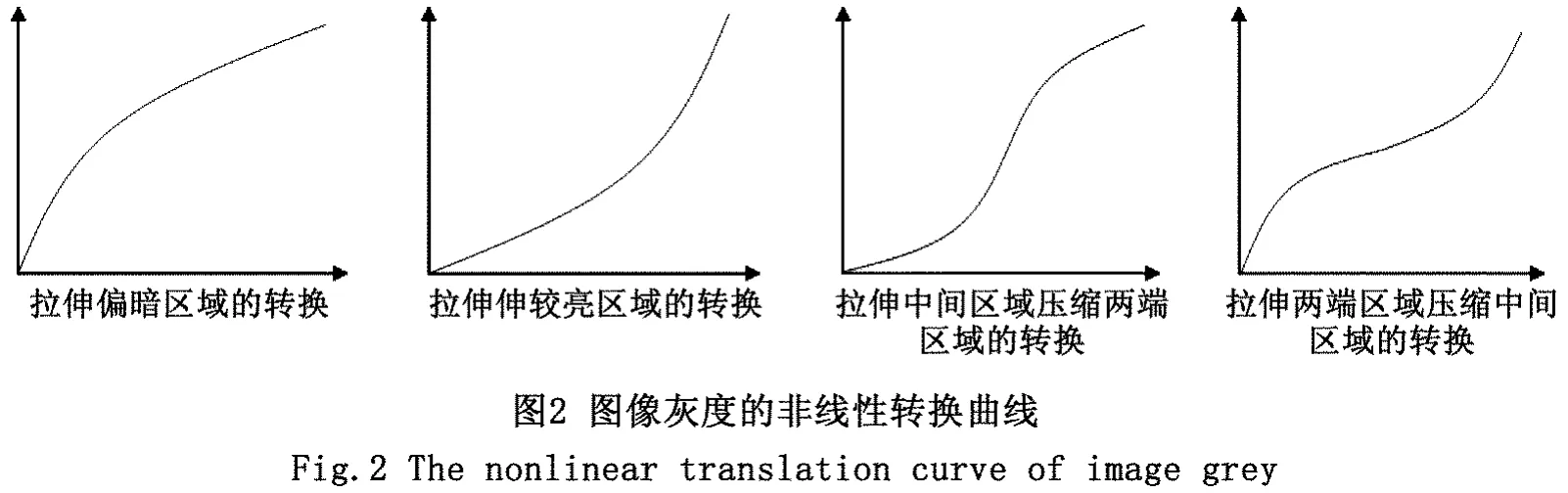
图像增强就是要提升图像质量，即要把指定的局部图像特征更加突出、改善降质图像的质量。在实际中存在较多的就是图像对比度降低，往往表现为部分区域偏亮、偏暗或灰度比较集中，四种典型的非线性转换曲线如图2所示，横坐标表示原始图像的灰度，纵坐标表示处理后图像的灰度［10－11］。

Tubbs提出了一种归一化的非完全Beta函数自动拟合图像增强的四类变换曲线

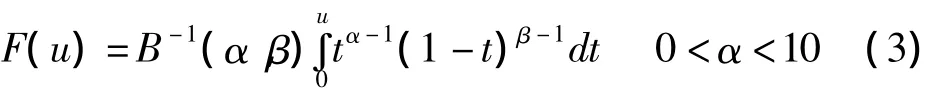
式中B(á，â)－Beta函数，其定义为B(α，β)=∫1

0tα－1(1 －t)β－1dt。

对应不同的á，â值，非完全Beta函数F(u)具有不同的变换曲线，本文利用提出的算法自适应地确定待处理图像变换函数最佳á，â值。设原始图像f(x，y)，(x，y)∈Ù为图像的定义域，增强后的图像为f'('x，y)，(x，y)∈Ù。首先，我们对图像灰度值进行归一化处理

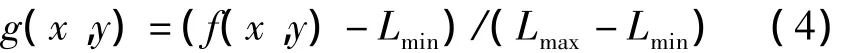
式中Lmax和Lmin－图像灰度值的最大值和最小值。

对归一化的原始图像进行变换

利用提出的算法确定变换函数F(·)的最佳参数á，â值，将增强变换后的图像反归一化处理，即得输出图像f'('x，y)

本文采用测量函数(7)作为评价图像非完全Beta自适应增强效果的判别标准，其定义为

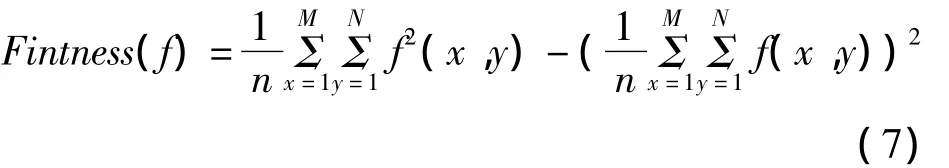
式中M和N－图像的长和宽;f(x，y)－图像第(i，j)个像素的灰度值;n=M×N－原始图像像素点(x，y)广义变换后的灰度值。

2.2 自适应趋向因子

细菌觅食优化算法的参数较多，包括:种群大小，游动的步长单位，趋向性、复制和迁移操作的执行次数以及迁移概率和每次向前游动的最多步长数等。算法的优化性能和收敛速度与这些参数值的选择紧密相关［9］。在这些参数之中，比较重要的一个参数是趋向因子C，趋向因子用来对不同细菌进行游动步长的调节，而一般情况下，所有细菌都采用相同的单位趋向移动步长，游动步长不应小于某一特定值但是如果取值太小，虽然在某种程度上可有效地避免算法过早收敛而增加逃离局部最小值的能力，但对于远离极小值的细菌不利于快速收敛;如果趋近因子C取值过大，虽然对于远离局部极小值的细菌可以加快收敛，但是对于极小值周围的细菌会使其跳过极小值而减小算法的精度，因此可以看出，趋向因子C在保持种群的多样性和提高算法的收敛性能中起着重要的作用。基于以上讨论，我们提出了根据细菌位置情况而自适应改变的趋近因子，如下式所示

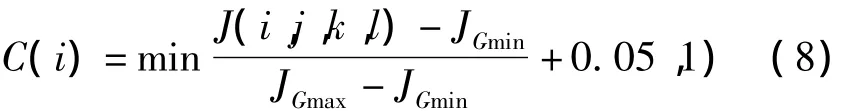
式中JGmin－目前群体所发现的最佳位置;JGmax－所有细菌经过各自的最佳位置中最坏的位置。

可以看到，当细菌位置距离局部极小值较近时，细菌具有较小的趋向步长，因而具有很好的趋近极小值的能力;当细菌位置距离局部极小值较远时，细菌具有较大的趋近步长，因而具有很好的快速搜寻极小值的能力。因此，本文提出了基于自适应细菌觅食优化非线性完全beta函数的图像增强算法，算法的主要实现步骤描述如下:

［步骤 1］ 初始化参 数:n，N，Nc，Ns，Nre，Ned，Ped。

n:搜索空间维数，N:细菌种群个数，Nc:趋向次数，Ns:游动次数，Nre:复制次数，Ned:迁移次数，Ped:迁移概率。

［步骤2］迁移循环:l=l+1。

［步骤3］复制循环:k=k+1。

［步骤4］趋向循环:j=j+1。

(a)对于每个细菌i=1，2，…，N进行如下的趋向运动。

(b)计算每个细菌的适应度j(i，j，k，l)。

(c)保存当前轮最优值Jlast=J(i，j，k，l)。

(d)翻滚:在－1到1之间产生一个随机向量Δm(i)，Δ(i)∈Rn，m=1，2，…，p。

(e)移动:θi(j+1，k，l)=θi(j，k，l)+C，计算J(i，j+1，k，l)，否则tm=Ns。

(h)如果i≠N，下一个细菌继续从［b］执行。

［步骤5］如果j＜Nc，进入步骤3。

［步骤6］复制。

对于每个细菌i=1，2，…，N，计算其能量

(f)计算J(i，j+1，k，l)。

(g)游动。

i)初始化游动长度:m=0。

ii)当m＜Ns，m=m+1，如果J(i，j+1，k，l)＜Jlast，那么Jlast=J(i，j+1，k，l)，同时θi(j+1，k，并按能量排序。

淘汰掉Sr个能量低的细菌，Sr个能量高的细菌进行复制。

［步骤7］如果K＜Nre，进入步骤。

［步骤8］迁移:对于每个细菌i=1，2，…，N，生成随机数Rand，如果Rand＜Ped，则对该细菌在寻优区间内进行初始化，如果l＜Ned，则进入步骤2，否则结束。

3 仿真实验及讨论

为了检验算法的效果，我们使用一副降质图像‘peppers’进行验证，其灰度级均为256级。而且我们用标准的细菌觅食算法和所提出的算法进行比较，他们的参数如表1所示。图3显示了用标准BFA和提出的ABFA对降质图像‘peppers’进行Beta函数优化的过程，表2列出了两种算法提炼出的非完全Beta函数参数和适应度，可以看出本文提出的ABFA算法收敛速度快比BFA更快，得到的适应度函数值更高。

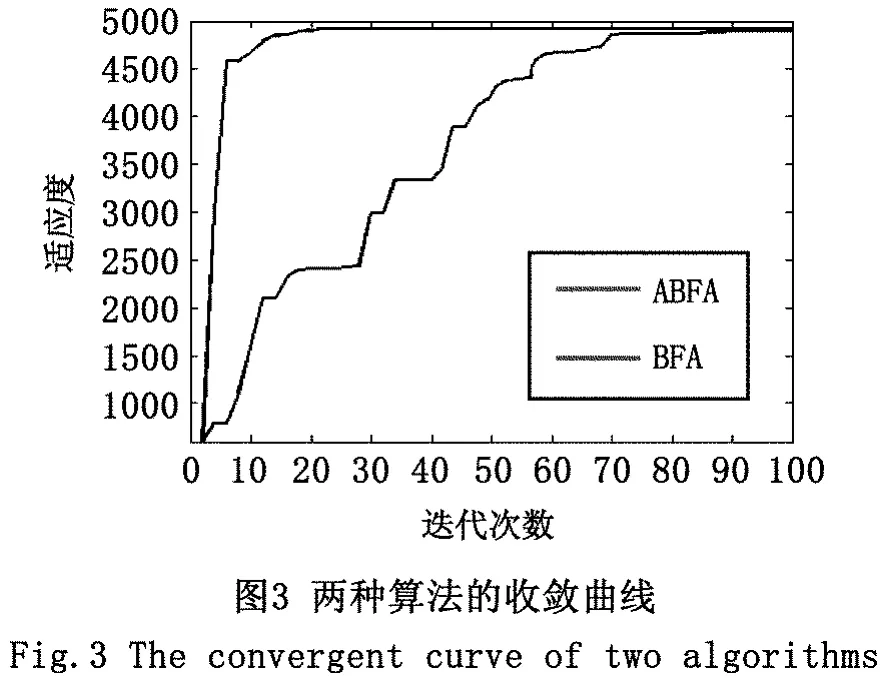
表1两种算法的参数Tab.1 The parameters of two algorithms

表2两种算法用于Beta函数的结果对比Tab.2 The result comparison of two algorithms for Beta function

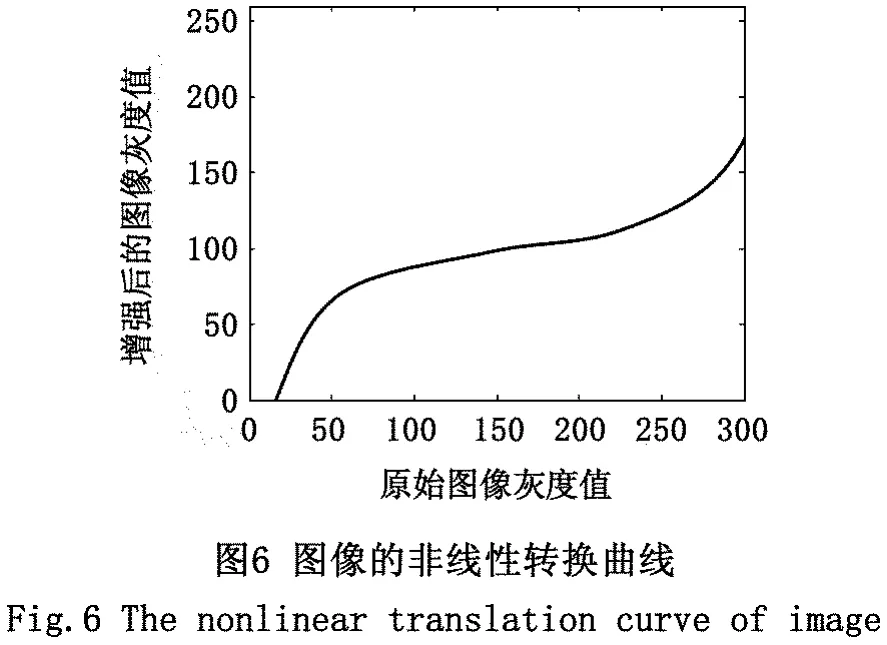
图4分别为原始降质图像及其用ABFA优化Beta函数的图像，图5是对应这两种图像的柱状直方图，图6是对应ABFA优化Beta函数后图像对应的非线性转换曲线。可以看出，原始降质图像过于明亮，并且明暗界限不明显，尤其是“青椒”明显失去了立体感，对应的直方图两边稠密中间稀疏，视觉效果差。使用本文所提出的方法增强图像后，图像明暗自然，轮廓清晰，“青椒”的立体感比较强，更有光泽。从对应的直方图来看，图像灰度范围分布更均匀，明暗灰度区域分配更合理，其视觉效果有明显的改善。从图6来看，本文提出算法对应的非线性变换函数的曲线对应图2中的第四类，原始的降质图像灰度普遍偏亮，增强后的图像拉伸了两端区域并且压缩了中间区域，这与直方图的变化是一致的。

4 结论

本文提出的算法具有较强的寻优能力，应用于非完全Beta变换函数对图像进行自适应的增强处理，能够根据原始图像的灰度自适应的调节图像的灰度值。实验结果表明，该算法收敛速度快，

精度高，可以获得较好的Beta函数参数，从而获得一条最佳的灰度变换曲线，获得了非常好的增强效果，增强后的图像更符合人的视觉感受。

［1］李丙春，耿国华.基于粒子群优化的图像自适应增强方法［J］.计算机工程与设计，2007，28(20):4959－4961.

［2］LEE JD.Digital image enhancement and noise filler by use of local statistics［J］.IEEE Trans I’AMI，1997，19(9):863－872.

［3］CHENG H V，XU H.A novel fuzzy logic approach to contrast enhancement［J］.Pattern Recognition，2000，33(5):809－819.

［4］TUBBS J D.A note on parametric image enhancement［J］.Pattern Recognition，1997，617－621.

［5］张斌，蒋丽峰，蒋加伏.一种图像增强的自适应免疫遗传算法［J］.计算技术与自动化，2005，24(3):54－56.

［6］PASSINO K M.Biomimicry of bacterial foraging for distributed optimization and control［J］.IEEE Control Systems Magazine，2002(22):52 －67.

［7］SWAGATAM DAS，ARIJIT BISWAS，SAMBARTAa DASGUPTA.Bacterial foraging optimization algorithm:theoretical foundations，analysis，and applications［J］.Foundations of Computational Intelligence，2009(3):23 －55.

［8］DATTA T，MISRA I S.Improved adaptive bacteria foraging algorithm in optimization of antenna array for faster convergence［J］.Progress in Electromagnetic Research C，2008，1(1):143－157.

［9］周雅兰.细菌觅食优化算法的研究与应用［J］.计算机工程与应用，2010，46(20):16－21.

［10］孙勇强，须文波，孙 俊.基于量子行为微粒群优化算法的图像增强方法［J］.计算机应用，2008，28(1):202－204.

［11］蒋丽峰，杨亚蕾，张顺淼.一种新型免疫遗传算法在图像增强上的应用［J］.福建工程学院学报，2007，5(1):71－74.