与判断矩阵一致性无关的单准则排序法*

刘开第，金 斓 ，庞彦军，马立涛

(河北工程大学不确定信息研究所，河北邯郸056038)

单准则排序是指，在单一准则C下对n个对象按重要性大小排序。单准则排序的困难首先是，因为没有秤靠决策者判断所以有无法回避的不确定性，必须合理确定并定量表征这种不确定性才可能正确排序。

层次分析法(AHP)［1－3］用“两两比较”的方法，在引入一种称为比例标度的相对标度概念基础上，通过构造两两比较的“1－9”比例标度判断矩阵很好地解决了单准则排序中不确定性的确定与定量表征问题。合理确定不确定性的关键是“两两比较”和“比例标度”。

关键1:两两比较:在社会与经济系统中，决策属性的重要性通常具有相对性，因为没有一种绝对标度来度量这种相对重要性只能通过“比较”才能显现重要性的不同。由于三个对象排序时“甲胜乙，乙胜丙而丙又胜甲的连环套”并不鲜见，所以只“比较”不够、还必须进行“两两比较”。对于个数不是非常多的定性因素来说，“两两比较”是正确排序的基本准则，这是由事物的复杂性和人们认识的局限性决定的。

关键2:比例标度:对象i与j在准则C下进行一次重要性比较时，比较结果的表征严格讲与对“重要性程度”的等级划分有关，因为人们是按着“重要性程度的等级”去区分所论重要性的不同。由于人凭判断最多只能区分开九个不同的重要性等级，这是为心理学试验所证实了的。

所以重要性程度的“九级划分”是人凭判断所能进行的最精细划分。当然根据需要与可能也可采用“七级划分”、“五级划分”，甚至“三级划分”，只要给出的“等级划分程度”能满足解决实际问题的需求即可;高级划分比低级划分的好处是有更强的区分力，如当“三级划分”不能把对象i与j所属的重要性区分开时，那么五级、七级或九级划分则可能把i与j的重要性区分开。

以九级划分为例，若用1－9这九个数字依次表示九个重要性等级的量化值，那么当i与j在准则C下进行一次重要性比较时，用ai表示对象i属于第ai个重要性等级，用aj表示对象j属于第aj个重要性等级，则ai与aj都是1－9中的某个数字;由于比值ai/bj可清楚地表征对象i与j的重要性差别，所以比值ai/bj是一种度量“相对重要性”的标度，称之为比例标度。显然比例标度是一种相对标度;相对标度与米、秒等绝对标度的区别是，没有明确的物理意义。相对标度概念的引入和应用是层次分析法的一大贡献，也是系统分析的一大突破。

对象i与j在准则C下进行一次重要性比较时可用比例标度ai/bj表征比较结果，而n(n≥3)个对象在准则C下“两两比较”一次共可比较n2次(包括“自比较”，并且i与j比较以及j与i比较看作是两次比较)，这n2个用“1－9”比例标度ai/bj表征的比较结果，构成一个n×n矩阵。

称该矩阵为两两比较的“1－9”比例标度判断矩阵，简称判断矩阵。比例标度ai/bj中的ai与aj是对象i与j在准则C下进行一次重要性比较时各自所属的重要性等级，因而都是1－9这九个数字中的一个。

比例标度判断矩阵An是确定并定量表征单准则排序不确定性最具优势的表达形式，之所以被广泛采用不只是因为这种表达形式极具公平性、合理性和可操作性，而且有利于由此构建单准则排序方法。所以可视为是已达成共识的单准则排序的初始数据条件。

当构造了比例标度判断矩阵An=(ai/bj)n×n后，那么任意两个对象i与j的重要性比较结果都是一个确定的实数，所以，n个比较对象在准则C下的重要性排序是确定的，由判断矩阵An中的数据决定。如果认同这一点，这意味着如果对象i的排序度量为μi(C)，那么客观上必存在映射Fi，可实现由An表征的数据到排序度量μi(C)的转换，即

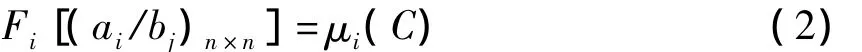
俗称μ(C)为重要性权重，且μi(C)满足

这样，单准则排序就是根据判断矩阵An中的数据，具体构造映射Fi的数学表达式。但是，当构造了判断矩阵An后，是否认可比较对象的排序由判断矩阵An中的数据决定是一个至关重要的问题，它涉及两种本质不同的单准则排序理念。

层次分析法(AHP)，不认为An中的数据能正确确定n个比较对象的排序，还要再增加一个条件:即An还必须满足“一致性检验”。当An满足一致性检验条件时，认为An的最大特征根λmax对应的特征向量“归一化”后，就是n个比较对象的真实排序;否则，如果An不满足一致性检验条件，则认为An不能提供合乎逻辑的排序，因而必须对An进行调整。

“一致性检验和调整判断矩阵”是AHP给出的单准则排序方法的核心。在已有的单准则排序方法中被广泛认可并被广泛采用的正是层次分析法(AHP)给出的基于一致性检验的单准则排序方法。一致性检验的单准则排序方法如下:

如果判断矩阵An=(ai/bj)n×n的最大特征根λmax满足

则认为判断矩阵An=(ai/bj)n×n的一致性程度是可以接受的，判断矩阵的一致性程度是可接受的是指，认为判断矩阵是保序的，亦即认为判断矩阵An=(ai/bj)n×n的最大特征根λmax对应的特征向量经“归一化”后就是n个比较对象的真实排序，其中R.I.是Saaty教授定义的平均随机一致性指标［2－3］。

如果C.R.＜0.1不被满足，AHP认为判断矩阵An(ai/bj)n×n偏离一致性程度过大、“判断”没能趋于一致;认为没趋于一致的“判断”不能得到合乎逻辑的排序，所以必须调整判断矩阵。实际应用中当C.R.＜0.1不被满足时都对判断矩阵进行调整。用最大特征根对应的特征向量对比较对象排序的方法称为特征根法。特征根法是层次分析法最重要的排序方法。除此外，常用还有最小二乘法、对数最小二乘法、最小偏差法、以及梯度特征向量法等［2－3］，所有这些排序方法都建立在一致性检验基础上。基于一致性检验的单准则排序方法源于下面两个基本事实:

1)在比例标度判断矩阵An=(ai/bj)n×n中，如果任意i行j列元素aij与 行列元素aij之积都恰好等于i行k列元素aik，即aij·ajk=aik。则称判断矩阵An是严格一致性矩阵。

容易证明，如果比例标度判断矩阵An是严格一致性矩阵，那么An的最大特征根λmax=n而其它特征根全为0，并且最大特征根λmax=n对应的特征向量“归一化”后，一定是判断矩阵中n个比较对象的真实排序，序向量中第i个分量λi是第i个排序对象的权重。

2)应用中的An通常都不是严格一致性矩阵。由Perro定理知，任意比例标度判断矩阵An如果不是严格一致性矩阵，那么An的最大特征根λmax一定比n大，并且λmax对应的特征向量一定是正向量。因为当λmax－n越小时，表明判断矩阵An具有的“一致性程度”越大，所以当判断矩阵An的一致性大到“一定程度”时，虽然λmax对应的特征向量“归一化”后不一定是n个比较对象的权重向量，但却有可能不改变n个比较对象的重要性排序。

如果An的最大特征根λmax对应的特征向量归一化后的排序与λmax=n时对应的特征向量归一化后的排序一致，则称判断矩阵An是保序的。这样，如果能判定An是保序的，那么n个比较对象的重要性排序就是:An的最大特征根λmax对应的归一化的特征向量。那么，比例标度判断矩阵An(ai/bj)n×n满足怎样的条件才是保序的呢?Saaty教授凭经验给出的条件就是

1 .基于一致性检验排序的不足

1.1一致性检验标准的不严谨性

一致性检验标准

中得临界值“＜0.1”是Saaty教授凭经验确定的，缺乏必要的理论依据［2－3］。一致性检验标准中的临界值是界定An是否保序的依据，具有如此重要作用的数据缺乏必要的理论依据本身就是问题。现在看来，界定判断矩阵An具有怎样的“一致性程度”才是保序的，这是一个非常困难的问题，一是选择到合用的“一致性指标”并不容易，二是希望确定一种具有理论支撑的一致性指标的某种“临界值”、作为检验判断矩阵An保序应具有的一致性程度，是不现实的，原因是，虽说判断矩阵An的保序性与“一致性程度”间有一定关系，但是An具有怎样的“一致性程度”才是保序的，决策者几乎无法知道;其困难程度远比排序大。

1.2调整判断矩阵排序理念的片面性

当一致性检验标准“C.R.＜0.1”不被满足时，认为判断矩阵不能提供合乎逻辑的排序，所以必须对判断矩阵进行调整。这是层次分析法(AHP)关于单准则排序的实质性排序理念，到目前为止，虽有不少对单准则排序的改进方法，却都没有对“调整判断矩阵的排序理念”提出过疑意;改进排序方法的重点是，如何使构造的比例标度判断矩阵容易通过一致性检验和减少调整判断矩阵的盲目性［4－6］。“C.R.＜0.1 ”不被满足相当于在An中出现“甲胜乙、乙胜丙而丙又胜甲”的反序情况。实际上反序也是一种客观存在，不只是在各种竞技项目中“弱可能胜强”，即使在社会经济系统中、在特定情况下“弱也可能胜强”;所以一旦在An中出现反序，并不意味着一定是决策者在判断上出了问题、一定是犯了逻辑错误;也可能是在特定情况下、决策者对可能发生的“弱胜强”的正确预判。正因为“反序”允许出现在决策者的判断中，所以一旦An中出现反序，未必允许对判断矩阵进行调整，而相信决策者判断也不失是一种正确的选择。所以，认为“一致性检验”不被满足时必须调整判断矩阵的排序理念是值得商榷的，正确的选择应是:“在相信决策者的判断与对判断矩阵认真复核之间”作出选择。但必须考虑到判断矩阵的“不可预知性”和“不可重复性”。特别是，当“一致性”检验不被满足时，An中比较对象的排序仍然是确定的，并且决策仍需知道这种真排序。但是，一旦对判断矩阵An进行了调整，那么基于一致性检验的排序方法再也无法知道An调整前的真实排序。单从这一点看，基于一致性检验的单准则排序也不能涵盖所有单准则排序问题。

事实上，只要不把An的最大特征根λmax对应的特征向量“归一化”后看作是比较对象的排序，那么，就无需对判断矩阵An进行一致性检验。原因是，An中比较对象的排序由An中得数据决定，与An是否“保序”以及具有怎样的“一致性程度”并无关系。严格讲验证An中数据的可信性是构造An的任务，并非是依据An中的数据对比较对象排序的研究内容。问题是，能否依据An中的数据在一致性检验之外找到对比较对象排序的排序方法，回答是肯定的。

2 .由判断矩阵数据决定的单准则排序

2.1评分标度

已知比例标度判断矩阵为An=(ai/bj)n×n，因为给定An后，n个比较对象的排序已没有不确定性，由An中的数据决定。问题是，对象i与j在准则C下进行一次重要性比较时的比例标度ai/bj，对于不同对象j并不具有可加性，所以当对象i在与n个对象各进行一次比较后对象i的相对重要性大小决策者是不知道的。这是比例标度这种“相对标度”的不足，为此引入一种称为评分标度的新的相对标度概念。

评分标度是在准则C下对n个比较对象按重要性大小排序的常用方法。如果用μij表示对象i与j在准则C下进行一次重要性比较时i的得分，用μij表示对象j的得分，那么要想保证评分的公平性，必须规定，i与j的得分和为常数m，即μij+μji=m(m为常数)。

通常m是单值常数，但也有例外;如足球比赛中，规定一场比赛胜方全取3分负方不得分，而平局时则比赛双方各得1分。在此m可为3也可为2，这种规定是为了鼓励“取胜”。在一般情况下m只是一个常数。此时以m=1为最简。规定μij+μji=1，显见评分标度μij是一种相对标度。并且显然评分标度具有“可加性”，亦即对象i关于多个对象j的比较得分可以相加。

当对象i与j在准则C下进行一次重要性比较时，如果直接在［0，1］区间上选择一个实数μij作为对象i的得分，那么要想保证评分的合理性并不容易，所以直接从［0，1］区间上选择μij并不具有实际的可操作性。但是，当对象i与j在准则C下进行一次重要性比较时，用比例标度ai/bj作为比较结果却有公平性、合理性和实际的可操作性。这样问题就归结为:能否把不具有“可加性”的比例标度ai/bj转化为评分标度μij。

这样就涉及到两种“相对标度”转换问题:一是两种标度能否转换，二是怎样的转换能保证得到的评分标度符合人凭判断的打分逻辑。两种标度可以转换是不言而喻的，因为比例标度ai/bi与评分标度μij都是对象i与j在准则C下进行一次重要性比较时，为把i与j的重要性差异区分开的一种“相对标度”。这样的两种“相对标度”理应能转换。剩下的问题是，怎样的转换公式得到的评分μij符合人凭判断打分的打分逻辑。标度转换公式如下。

2.2比例标度到评分标度转换

已知两两比较的1－9比例标度判断矩阵为An=(ai/bj)n×n。当对象i与j在准则C下进行一次重要性比较时，用实数μij表示i的重要性得分，用μij表示j的重要性得分。令

［0.1，0.9］与之对应，当i=j时，μij=0。

转化为区间［0.1，0.9］上的评分标度μij，那么该转换公式是否合理，亦即能否得到满足用户需求的某种评分规则，是评分排序是否可行的基础。

2.3标度转换公式的合理性分析

衡量变换式(8)的合理性是指，当对象i与j在准则C下进行一次重要性比较时，由公式(8)得到的对象i的重要性得分μij，是否符合人凭判断打分的打分逻辑分析如下。

1)当对象i与j进行一次重要性比较时，我们的目的是把i与j的“不同重要性合理区分开”，按这种目的“自比较”没有意义。因为允许自比较时，最强与最弱的对象在自比较时，都将不加区分的获得0.5分，只要对象i与j的重要性不同，那么各自增加0.5分的实际效果，都是“人为”缩小i与j的重要性差距;显然这与把i与j的“重要性”区分开的目的相悖。所以，不管实际问题中研究对象能否进行“自比较”，但在使用评分标度时一律不允许“自比较”，或说“自比较”不得分，这是评分排序的特点，也是评分标度与比例标度的区别之一。所以规定μij=0是合理的。

2)如果i≠j，当ai/bj=1时表明i与j同等重要，同等重要的两个不同对象比较一次各得0.5分是合理的。

3)如果i≠j，当ai/bj=9时表明i极端强且j极端弱，规定极端强与极端弱的对象比较一次，强者得0.9分而弱者得0.1分，刚好九个等级，是人凭感官和判断能区分开的最多等级，所以是合理的;反之超过9倍的得分差距从心理学角度将被视为不合理。

4)对象i从“i与j同等重要”到“i比j极端重要”的变化过程，在没有特定条件下认为i的重要性得分呈线性增加符合人们的打分直观，所以当i≠j且1≤ai/bj≤9时经线性插值规定

是合理的。

5)当i≠j且1/9≤ai/bj＜1 时规定

是为了保证在i≠j时μij+μji=1。

至于为什么不选择在区间1/9≤ai/bj＜1上用线性内插法确定μij而选择区间1≤ai/bj≤9，是因为区间1/9≤ai/bj＜1比区间 1≤ai/bj≤9的间距短，评分变化快，因而由此得到的评分在直观上效果稍差。

上述五条表明，由变换式(8)从比例标度得到的评分规则，在没有特殊要求的条件下是合理的，因而是一种合乎逻辑的用户需求。

2.4评分排序法

标度转换式(8)将比例标度ai/bj转化为评分标度μij，同时把比例标度判断矩阵An=(ai/bj)n×n转化为评分标度判断矩阵Bn=(μij)m×n。

评分判断矩阵Bn=(μij)m×n的第i行j列元素μij是对象i与j在准则C下进行一次重要性比较时对象i的得分，与此同时j行i列的元素μij是j与i进行一次重要性比较时对象j的得分，并且当i≠j时满足μij＞0，μji=1=μij。易见，Bn=(μij)m×n的第i行元素之和fi是对象i的得分和。

在总共n2次两两比较中，除有n个μij=0外，余下的n(n－1)次“两两比较”中共合得1)分，所以每个对象i的得分率为

得分率向量为

并且η(c)就是n个比较对象的排序向量，向量中第i个分量ηi(c)是对象i的排序度量，俗称ηi(c)是对象i的重要性权重。按得分率对比较对象排序其正确性是不言而喻的，当然前提条件是获取到得评分是公平、合理、惟一的。至此，在没考虑比例标度判断矩阵An=(ai/bj)n×n是否保序以及具有怎样的一致性程度情况下，直接从矩阵中数据出发，通过标度变换用评分排序法解决了矩阵中n个比较对象的排序问题。显然评分排序与比例标度判断矩阵An是否保序以及具有怎样的一致性程度没有关系，它由矩阵中的数据决定。

从比例标度判断矩阵An=(ai/bj)n×n出发，到完成评分排序，只用到加乘运算。所以评分排序算法要比基于一致性检验的特征根排序法简便很多。

3 例子

三个橄榄球队打一次循环赛，A1，A2是由两两比较的1－9比例标度判断矩阵表征的，关于比赛的两种预测。A1，A2分别为

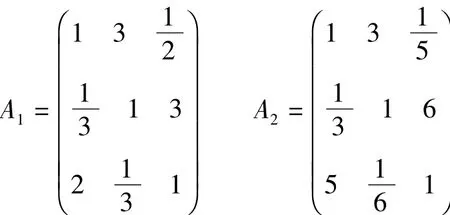
求两种预测下的比赛排名。

显见在A1与A2中都存在“甲胜乙，乙胜丙而丙又胜甲”的反序情况。一致性检验结果如下:

对A1的检验结果为

最大特征根λmax=4.002

对A2的检验结果为

两个判断矩阵都不满足C.R.＜0.1，按照一致性检验的排序理念，生成两个判断矩阵的“判断”都没能趋于一致，不能提供合乎逻辑的排序，所以必须对判断矩阵A1，A2进行调整。但是，当判断矩阵中出现反序时，可认为是决策者在特定情况下，认为“弱可能胜强”的一种正确预测。所以，在反序情况下仍需确定比较对象的真实排序。在评分排序看来，比较对象的重要性排序由判断矩阵中的数据决定，与判断矩阵“是否保序”以及具有怎样的“一致性程度”无关。评分排序步骤是:

步骤1.由公式(8)将比例标度判断矩阵A1，A2分别转化为评分判断矩阵B1，B2:

步骤2.计算得分率:在B1与B2中甲、乙、丙的得分依次为

步骤3.按得分率排序

甲＞乙＞丙 乙＞丙＞甲

结果分析:

虽然比例标度判断矩阵A1，A2均不满足一致性检验条件，但是矩阵中的比较对象的排序是确定的，并且排序结果是比赛得分的合理反映。实际上，给定不同的比例标度判断矩阵，意味着经标度转换后比较对象可以获得不同的比赛得分，这样甲、乙、丙间的6种排序，均可出现。

4 结论

构造的比例标度判断矩阵An是否可信，是决策者在构造An阶段应解决的问题;并且一旦构造了An，那么排序就由An中的数据决定，与An具有怎样的“一致性程度”并无关系。当An保序时，

AHP把An的最大特征根λmax对应的特征向量“归一化”后作为比较对象的排序，其正确性毋庸置疑，但要从严格意义上界定An保序，却是十分困难的，至少现阶段很难做到;并且认为不满足一致性检验(即出现反序)的判断矩阵An不能提供合乎逻辑的排序，这种排序理念的合理性也值得商榷。所以依据判断矩阵An中的数据构造排序方法才是单准则排序的正常途径。

［1］SAATY T L.The Analitic Hierorchy Process［M］，Pittsbargh:University of Pitteburgh，1988.

［2］许树伯.层次分析法原理［M］.天津:天津大学出版社，1989.

［3］王莲芬，许树伯.层次分析法引论［M］.北京:中国人民大学出版社，1990.

［4］姚 敏.一种实用的模糊层次法［J］.软科学，1990(1):46－52.

［5］张吉军.模糊层次分析法［J］.模糊系统与数学，2000，14(2):80－88.

［6］刘胜，张玉廷，于大泳.小生境遗传算法修正三角模糊数互补判断矩阵一致性及排序［J］.系统工程理论与实践，2011，31(3):522 －529.