基于改进遗传算法的开关磁阻电机优化设计

吕品，张京军，张海军

(河北工程大学信息与电气工程学院，邯郸056038)

开关磁阻电机 (Switched Reluctance Motor，SR电机)具有结构简单、调速范围大、控制灵活等优点，使其具有强大的市场竞争力［1］。但SR电机的转矩脉动和噪声较大，在一定程度上限制了它的应用［2］。研究表明，作用在定子上的径向力是引发电磁噪音的主要原因［3－4］。由于SR电机径向力与电磁转矩之间的耦合关系及径向力自身的高度非线性，建立精确的径向力模型存在很大难度，目前的研究主要从控制优化方面来减振降噪。文献［5］在有限元分析的基础上得出了考虑磁饱和的数学模型，但基于有限元的分析方法影响了计算的快速性。文献［6］建立了基于麦克斯韦应力法的数学模型，但由于采用的磁饱和矫正公式，其准确度还有待提高。文献［7］将麦克斯韦张量法和磁路法相结合，建立了无轴承开关磁阻电机的径向力模型，经仿真验证，该模型能较好的符合实际电机实际运行状态。在此基础上，本文使用结合布劳威尔不动点定理的改进遗传算法对SR电机径向力数学模型的进行优化，通过优化电机结构参数来降低径向力幅值。

1 遗传算法的改进

遗传算法模拟生物进化机制的一种现代优化方法，具有较强的鲁棒性及良好的并行性，已在系统优化设计、工业工程、制造系统设计等诸多领域中得到广泛应用［8］。然而，遗传算法在实际应用中也存在一些问题，比如搜索效率低、没有客观的收敛判断准则等［9］。不动点定理是拓扑学里一个非常重要的不动点定理，它保证了对于一个拓扑空间中满足一定条件的函数F(x)在其解空间Rn内必定存在一个或更多的不动点［14］。运用此理论设计遗传算法的收敛判断准则，可以避免标准遗传算法因人为设置停止准则而无法收敛到全局最优解的缺陷。

1.1 问题转化

使用不动点理论对函数F(x)进行寻优，首先要将求最优解问题转化为不动点问题，若X*是F(x)的极值点，则▽F(x*)=0。令G:Rn→Rn，X∈Rn，构造函数G(x)=x－▽F(x)，将函数优化问题转化为不动点问题。

1.2 编码

由于实数编码在函数优化领域比二进制编码和Gray编码更为有效，本文采用如下形式的实数编码:{x，f(x)，yi，f(yi)，l(yi)}，其中x是个体变量，f(x)是x的目标函数值，yi为个体x的单纯形顶点，f(yi)为单纯形顶点yi的函数值，l(yi)是单纯形顶点yi的整数标号。

1.3选取适应度函数

适应度函数是个体的优劣程度的评价标准，改进后的遗传算法则根据单纯形顶点的标号信息来寻找全标单纯形，即最优解。因此定义适应度函数为个体承载单纯形顶点各分量的平方和。

1.4初始化种群

对解空间Rn进行单纯形剖分后，随机生成初始种群，计算每个个体的承载单纯形，并按照公式(1)进行单纯形顶点进行整数标号

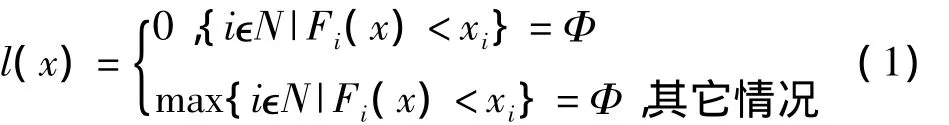
1.5施加增维算子

本文的改进遗传算法设计了增维算子。依据寻找不动点的方法，算法按照转轴运算产生一个维数不断增加的单纯形序列σ1、σ2、σ3…，由初始单纯形开始直至搜索到具有n维标号的全标单纯形。同时，将新一代个体的剖分网径缩小为父代个体的一半，按照公式(2)计算个体承载单纯形顶点，逐渐提高算法的精细度。

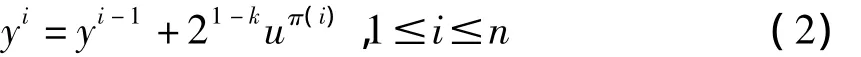
其中，π为N={1，…，n}的一个置换;ui为的Rn基底坐;k为算法的进化代数。

1.6施加交叉算子

交叉操作结合来自父代种群中的信息产生新的个体，是新一代个体的重要来源，本算法将父代按照个体承载单纯形的标号信息进行分类，根据“禁止近亲繁殖”的原则对不属于同一类承载单纯形的个体进行交叉操作。

1.7施加变异算子

本算法采用均匀变异来保证群体的多样性，同时对非全标单纯形中的个体优先变异。

1.8施加选择算子

选择算子用来确定从父代群体中选择哪些个体遗传到下一代群体中，以保证全局收敛性及算法效率，本算法按父子混合杰出者选择策略对种群施加选择算子，父代中的全标单纯形个体直接进入子代种群。

1.9判断收敛准则

当种群中的个体承载单纯形全部成为全标单纯形时，算法终止，输出的全标单纯形即为近似不动点，其对应函数值为最优值。

2 SR电机径向力模型的优化

2.1 目标函数

SR电机运行过程中的电磁力分为切向力分量和径向力分量。切向力是使电机运行的动力，产生电机运行所需要的电磁转矩。径向磁吸力不能产生电机旋转所需要的电磁转矩，而且力图压缩定、转子间气隙壳体结构，使定子不可避免地形成压缩变形，进而引起电机振动和噪声。因此，降低径向电磁力有助于减轻SR电机运行产生的振动和噪音。

本文将文献［7］建立无轴承SR电机径向力的数学模型的麦克斯韦应力法应用到普通的SR电机径向力建模，消除悬浮绕组产生的悬浮力的影响，建立径向力的目标函数:

其中 μ =μ0μr

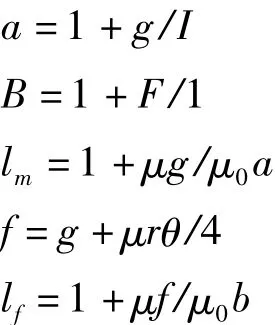
式中，F(X)－径向力函数，N;μ0－空气磁导率，μ0=4π ×10－7H/m;μr－ 材料相对磁导率;N－每相绕组匝数;I－每相通电电流，A;g－平均气隙长度，m;f－边缘磁通路径的平均长度，m;l－转子轭与定子轭的距离，m;r－转子外径，m;θ－为转子位置角，rad，定义为转子磁极偏离定子磁极的角度;Bsat－材料的饱和磁密，T。

2.2 优化变量

重点考虑对径向力影响较大的主要结构参数，选定转子外径r、每相绕组匝数N、气隙长度g三个变量为优化变量，记为X=［g r N］T。

2.3 约束条件

1)转子内外径比值。参照SR电机的设计经验，设定电机转子外径r与定子外径Ds的比值λ范围为:

2)每相绕组串联匝数。SR电机的每相绕组的匝数越多，绕组的电流峰值越小，对降低开关管的伏安容量有利;但匝数太多，会使电机的启动转矩降低，启动性能受到影响。综合考虑电机的槽满率、铜损及铁损，设定匝数N的范围

式中，Nr－转子极数;U －绕组端电压，V;θc－导通角，rad;n－电机转速，r/min;L－转子叠片长度，m。

3)气隙。为了获得较大的电磁转矩，减小功率变换器伏安容量，应尽量减小气隙;但气隙太小容易造成电机的振动和噪声。同时考虑安装工艺、加工工艺的限制，气隙的范围设在0.025 mm至0.5 mm之间。

3 算例分析

优化采用的电机参数:功率P=2.2 kw，转速n=3 450 r/min，定转子轭之距 l=0.032 m，定子外径 Ds=0.120 m，铁芯叠片长 L=0.062 m，定子级数NS=12，转子级数Nr=8，参考电流I=8 A，θ=14°=0.244 3 rad，定转子铁芯材料使用35W250－DW250－35(W09)硅钢片，其饱和磁密Bsat=1.77T，相对磁导率 μr=4100。

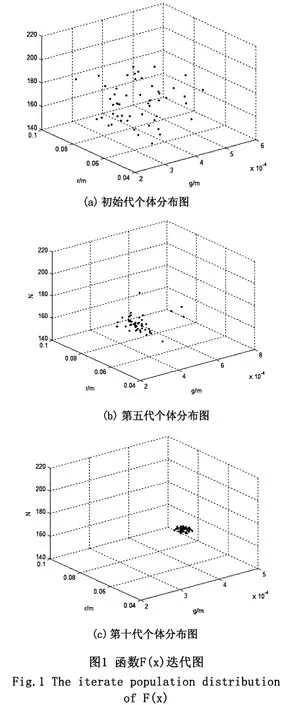
算法迭代过程的个体分布图见图1。首先在三维解空间R3中随机生成初始种群，其分布见图1－a，根据改进遗传算法流程，对种群反复施加繁殖算子，算法在第五代的种群分布见图1－b，个体已迅速收敛到最优解附近区域，显示了改进算法良好的收敛速度。最终算法在第十代收敛到全标单纯形(图1－c)，算法停止。对应近似最优解为(0.000 48，0.083，151)，函数值为 1 039.9。与标准遗传算法相比，迭代次数大幅减小，算法的效率得到极大的提高;利用承载单纯形的顶点信息作为判敛标准，避免了人为设置进化代数而不易到寻找最优解的缺陷。

优化前后电机的结构参数及径向力值见表1，可以看出，与原径向力值相比，通过改进的算法对SR电机主体结构优化后，电磁径向力下降了16.7%。可见，改进算法可以得到全局最优解，优化效果明显，适用于SR电机的结构优化。

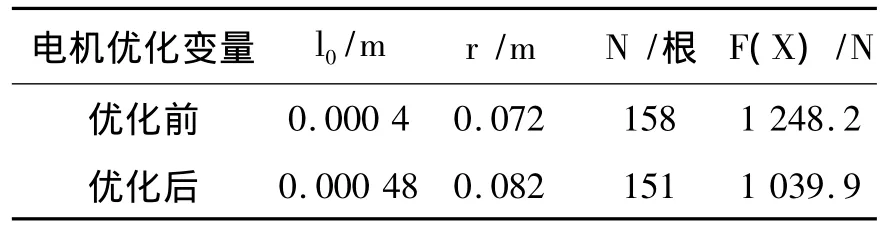
表1优化结果比较Tab.1 Comparison of optimum results

4 结语

本文针对SR电机实际应用中的存在的突出缺点，采用基于不动点算法的改进的遗传算法对电机的本体结构进行了优化设计。结果表明，改进后的遗传算法收敛速度快，稳定性高。同时通过电机实例验证了通过改进电机的主要结构参数能够较大程度地降低径向电磁力以及由此引发的振动和噪声。

［1］吴建华.开关磁阻电机设计与应用［M］.北京:机械工业出版社，2000.

［2］邳志刚.异步电机软启动的瞬时功率理论控制律［J］.黑龙江科技学院学报，2011，21(4):69－72.

［3］李争，郭智虎，张 玥.新型永磁转子偏转式三自由度电机磁场特性分析［J］.河北科技大学学报，2012，33(5):366－369.

［4］DIVANDARI M，KABIR M M.Acoustic noise reduction of switched motor drives［J］.Middle－ East Journal of Scientific Research，2011，8(6):1018－1026.

［5］TAKEMOTO M，CHIBA A.Radial force and torque of a bearingless switched reluctance motor operating in a region of magnetic saturation［J］.IEEE Transactions on Industry Application，2004，40(1):103－112.

［6］曹鑫，邓智泉，杨 钢，等.无轴承开关磁阻电机麦克斯韦应力法数学模型［J］.中国电机工程学报，2009，29(3):78－83.

［7］孙永鑫，胡春秀.大型电机线棒端部电场的有限元计算方法［J］.黑龙江科技学院学报，2012，22(2):25－29.

［8］韩明，周国强，王震洲.基于COM组件的电机转子绕组匝间短路故障诊断［J］.河北科技大学学报，2011，32(1):43－47.

［9］王小平，曹立明.遗传算法——理论、应用与软件实现［M］.西安:西安交通大学出版社，2002.

［10］陈焕，范志红，高瑞贞，等.基于不动点算法和k2(m)剖分的改进遗传算法［J］.河北工程大学学报:自然科学版，2011，28(2):56－59.

［11］王红霞，高瑞贞，张京军.基于不动点理论的改进遗传算法［J］.河北工程大学学报:自然科学版，2010，27(3):100－103.

［12］王宏民，全吉男，白玉成.基于模糊PID控制器的无刷直流电机调速系统［J］.黑龙江科技学院学报，2010，20(4):66－69.

［13］张京军，龙荣，张海军.开关磁阻电机径向力解析建模及有限元分析［J］.煤炭学报，2012，37(4):700－704.

［14］于国庆，张颖，李永伟.基于DSP的异步电机SVPWM控制系统及优化研究［J］.河北科技大学学报，2012，33(3):237－242.

［15］ZHANG J J，LONG R，ZHANG H J.Analytical and FEM modeling ofelectromagnetic radialforce for switched reluctance motor［J］.Applied Mechanics and Materials，2012(4):3765 －3769.