基于熵的灰关联模型在工程评标中的应用

王飞，陈鲜阁

(河北工程大学经济管理学院，河北邯郸056038)

工程项目的评标过程是比较常见的多层次目标决策问题，对于如何建立评标模型、构建指标体系以及用何种方法确定各指标权重，目前已有了不少的研究成果。在多数灰色关联的应用实例中，计算关联度时将各指标权重等权化，忽略了指标权重对整个评标模型的影响，使得最终评标结果不够精确。本文引入基于熵的灰色关联评标模型，应用熵权法计算各评价指标对整个评标模型的影响程度，业主方可建立灰色关联评标模型，分析并计算各投标单位与业主理想承包单位之间的关联度，由关联度的大小，使得业主能轻松选择最符合招标要求的投标方。该模型不但消除了指标等权化对评标结果的影响，而且考虑到了指标体系中各个指标之间存在的复杂隐形关联。本文将熵权法与灰色关联分析结合起来用于工程评标模型，不仅提高了“合理”度确定的客观性，同时也提高了工程评标过程中的评价精度，有利于招标单位确定中标单位。最后通过实例对该模型进行验证，得出结论，招标单位采用该评标模型在实际过程中可行，并且有一定程度的应用价值。

1 工程评标指标体系

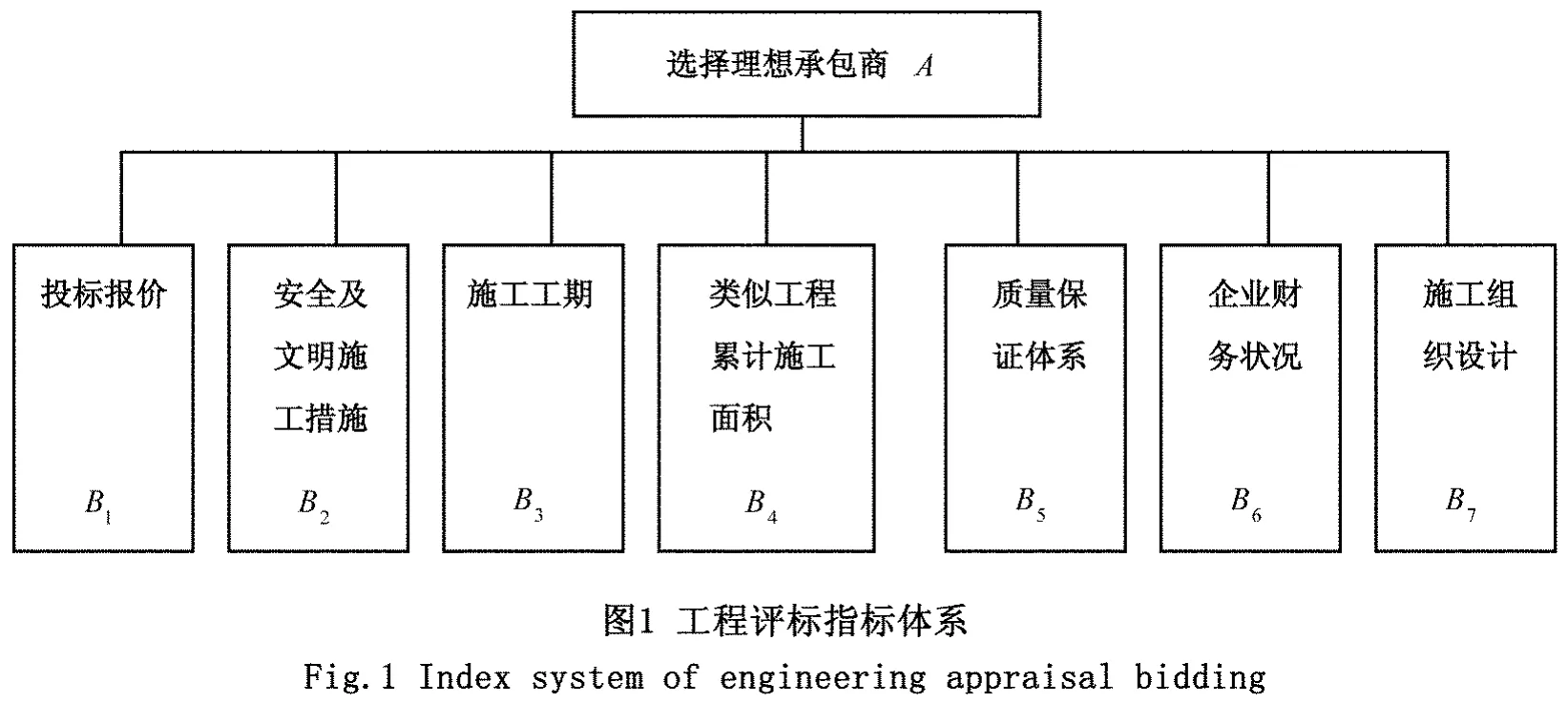
任何实际工程项目在进行评价时，都必须建立一套合适的评标标准体系作为业主评价投标单位的依据，而建立的这套评标标准体系与建立的评标数学模型并无直接联系。影响业主对投标单位的选择以及对业主利益有影响的要素均可选为工程评价指标，但对工程评标指标的选择必须要把握好区分主要指标与次要指标的度，只有这样才能使设置的评标指标体系具有可操作性。因此，遵循选择指标的针对性和技术与商务统筹考虑的原则，因此，遵循在选择指标时应将技术与商务综合考虑的原则，选择以下几个指标组成评标指标体系:投标单位的投标报价、投标单位的财务状况、投标单位提供的施工组织设计、施工工期、类似工程施工经验、安全及文明施工措施。如下图1。

2 基于熵权法的各指标权重计算

熵［1］(emtropy)最早是在热力学中由物理学家克劳修斯提出的，信息熵则是由申农(Shannon)将热力学熵引入信息论而引出的，多数应用于计算模糊评价中不确定性的度量。熵权值主要反映了信息间的无序化程度，其值越小，其效用值就越大;反之亦然［2］。对于由m个投标单位n个评标指标组成的初始矩阵，用熵评价所得有序度与效用确定指标权重，其计算步骤如下:

1)构建由m个投标单位提供的n个评标指标组成的指标值初始序列

2)将判断矩阵归一化处理，即消除各指标不同量纲对评价指标权重分配的影响，得到归一化判断矩阵B=(bij)mn。

式中xmax、xmin－评标指标中各指标下投标单位中的最理想者与最不理想者。

3)根据熵权法的定义，可以确定指标体系中各指标的熵值为

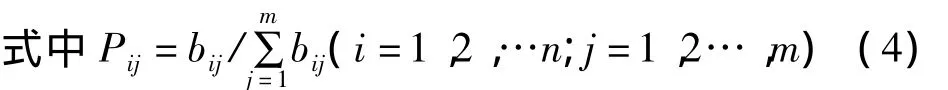
4)最终确定评价指标的熵权W。

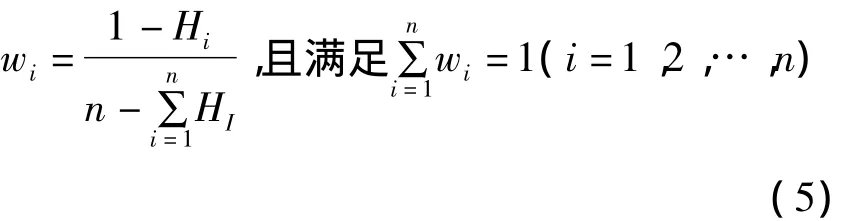
其中，wi为第i个指标的熵权;由此可得指标体系的熵权集:W=(w1，w2，w3，…，wn)。

3 灰色关联评标模型

灰色关联度模型［3］是一门研究信息模糊不清晰并带有不确定性的应用数学学科。灰色关联度评标决策模型的基本思路是:根据整个评标问题的灰色背景，找出理想施工单位对应的评价指标值，由决策问题中各个投标单位提供的的指标值与理想施工单位对应的指标值之间关联度的大小来进行评标问题中各投标单位的排序并确定最终承包单位［4］。

具体操作步骤如下［5］:

1)评价指标数列的确定:设有m个施工单位有意向参与投标，通过专家意见确定由n个相关指标组成指标体系，每个施工单位的所有指标构成一个数据列，称为原始数据列，记作:Xi(j)(比较序列)。

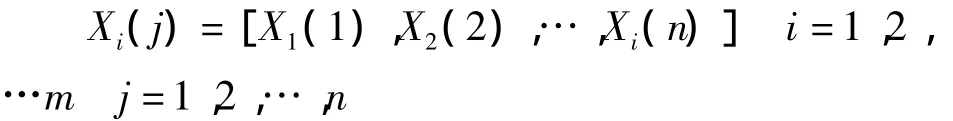
2)理想最优指标值序列的确定:从m个施工单位提供的相关指标的数据中，依从“效益型指标”取其最大值即投标单位的财务状况、投标单位提供的施工组织设计、类似工程施工经验、安全及文明施工措施这五个指标取原始数据的最大值，“成本型指标”取其最小值即对投标报价、施工工期的数据取最小值的原则，将选出的数据值组成序列;即:X0(j)(参考序列)。

3)指标序列初值化处理:评价指标体系中质保体系、报价、工期等指标具有不同的量纲，为消除这些对最终决策的影响，需要对各指标特征值作规范化处理。所谓规范化处理就是将各指标值初值化为0－1之间的数为最佳。初值化后的数列为X'、X'0。

4)计算关联系数:所谓关联程度，是指理想指标值与投标单位提供的指标数据之间的差别程度;关联系数ξ(Xi)的计算公式如下:

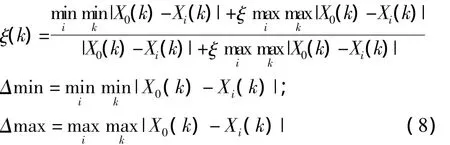
|X0(k)－Xi(k)|记为Δoi(k)。公式简化为ξ

5)确定指标权重向量(ωk)。

4 评标实例分析

青岛某住宅小区进行施工招标，共有5家符合条件的投标单位参与竞标，分别为:青岛建工A;中铁十局B;中铁四局C;青岛城建D;鲁王建工E。建设单位在评标过程中，主要是对商务标与技术标的评比。如图1所示，属于商务标的指标有:投标单位的投标报价、投标单位的财务状况;属于技术标的指标有:投标单位提供的施工组织设计、施工工期、类似工程施工经验、安全及文明施工措施［6］。相关计算步骤如下:

1)各投标单位提供的指标原始值如下表1所示。

2)指标原始序列初值化:确定理想指标值序列为 X0=(891.66，90，166，17.2，90，6 500，85)。将表1中的数据套用公式(5)(6)，得到初始化标准矩阵如表2。

3)计算关联系数:将数据套入公式(8)(9)中，得关联系数值如表3。

4)确定指标权重:将表2中的数据代入公式(3)(4)中，得评价各指标熵值为 H=(0.77，0.81，0.85，0.80，.076，0.82，0.62)。再根据公式(5)计算，得到各指标的熵权:W=(0.15，0.12，0.10，0.13，0.15，0.11，0.24)。

5)计算各投标单位的关联度大小:将所得的指标熵权与关联系数合并计算求得基于熵权的关联度为 ζ=(0.60，0.50，0.68，0.54，0.66)，即 γ3＞γ5＞γ1＞γ4＞ γ2。

由上述计算公式得出的指标权重结果可见，所选评价指标在评价过程中均占有相当大的权重，各指标都有较突出的代表性，本文所建立的指标体系对整个评标取得成功有积极的促进作用。而后由灰色关联决策模型用于评标过程的计算结果可知，各投标单位与业主理想承包商的相似程度排序为:中铁四局﹥鲁王建工﹥青岛建工﹥青岛城建﹥中铁十局，业主可根据这一评价结果选择最终中标单位。

表1投标单位评价指标值Tab.1 Evaluation Index of bidding units

表2初始化矩阵值Tab.2 Matrix value of initialization

表3关联系数值Tab.3 Correlation coefficient

5 结束语

熵作为指标权重的确定方法，可直接根据各待评价投标单位提供的指标值构成的判断序列来计算各个评价指标的权重，克服了凭人为主观赋于指标权重的主观随意性，也消除了等权计算关联度的不精确性对评标结果的影响。本研究通过加权的关联度来显示投标单位与理想单位的接近度，在利用灰色关联方法选择施工方时，最大限度地消除人为干扰的影响，为建设单位使用该模型选择中标单位提供了更为合理、准确的依据。

［1］李国良，付强.基于熵权的灰色关联分析模型及其应用［J］.水资源与水工程学报，2006，17(16):15 －18.

［2］王卓甫，张怡.基于熵权加权法的工程评标模型［J］.科技管理研究，2010(3):47－48.

［3］邓聚龙.灰色系统理论教程［M］.武汉:华中理工大学出版社，1992.

［4］石振武.基于模糊数学和灰色关联的工程项目评标方法研究［J］.森林工程，2006(1):55－57.

［5］潘妮，梁川.基于熵权的灰色关联度模型在流域水质综合评价中的应用［J］.中国农村水利水电，2008(4):1－7.

［6］刘 晴，王建平，王丛莹.基于灰色关联理论的建设工程评标方法研究［J］.工程管理学报，2010(2):153－155.