e-p等离子体中超强激光脉冲的分裂及类多孤子结构的形成
2013-03-15胡强林余晓光
胡强林,余晓光
e-p等离子体中超强激光脉冲的分裂及类多孤子结构的形成
*胡强林,余晓光
(井冈山大学数理学院,江西,吉安 343009)
通过推导并数值求解超强线极化脉冲激光在正负电子对(e-p)等离子体中传播时所满足的非线性Schrödinger方程,讨论了超强线极化脉冲激光在e-p等离子体中的传播特性。结果表明,传播过程中真空极化和磁化产生的非线性效应与群速度色散之间的竞争能导致高斯型脉冲激光的自压缩,对长脉冲,这种竞争能使脉冲在压缩后又会产生分裂,最终导致类多孤子结构的形成。
真空极化和磁化,正负电子对(e-p)等离子体,超强脉冲激光
0 引言
正负电子对(e-p)等离子体在宇宙环境下,比如吸积盘、脉冲星、中子星、黑洞等,广泛存在[1-4]。由于e-p等离子体存在环境的特殊性,到目前为止,人们对其性质所知甚少[3]。然而,e-p等离子体的性质对人们了解宇宙环境下e-p等离子体中发生的有关物理过程非常重要。因此,超强激光脉冲与e-p等离子体非线性相互作用的研究逐渐引起了人们广泛的关注[5-8]。近年来,超强脉冲激光技术的发展使在实验室环境下产生e-p等离子体成为可能。研究表明,用脉宽为10 ps,强度为1020W/cm2激光脉冲从两边同时轰击金薄膜靶,可以产生最高密度为固体电子密度的千分之一的正负电子对。若让轰击后产生的等离子体自由扩散,则由于正负电子的质量比离子质量小得多,在等离子体的外层可得到较纯净的e-p等离子体[4]。在实验室中用超强脉冲激光与高Z材料靶相互作用可以产生e-p等离子体,意味着人们在实验室中模拟宇宙环境成为可能,从而开辟了一条探索宇宙奥秘的新途径[5]。
超强激光与e-p等离子体非线性相互作用的研究对了解e-p等离子体中的一些物理过程非常重要,近十年来受到人们广泛的关注[6-8]。当激光强度比较低时,即小于1023W/cm2,相互作用中的非线性主要来自相对论效应和有质动力。但当激光强度达到1023~ 1026W/cm2时,一些新的相互作用机制开始显现。首先,辐射阻尼效应在相互作用过程中可能会起重要作用。不过有研究表明[9-10],在这一强度下,辐射阻尼效应对圆极化极化会起重要作用,而对线极化激光,这一效应可忽略。其次,在此强度下,电磁场的拉氏密度会产生非线性的扰动[11],此即所谓的量子电动力学(QED)效应。由于QED效应的出现,相互作用过程中将有一些新的物理过程出现,如光子反冲效应,正负电子对的产生等。这些过程,尤其是雪崩型正负电子对的产生将吸收大量的激光能量。固然,对单激光脉冲,这种雪崩效应只能在相当高强度(~1028W/cm2)时才能发生[12],但远在此强度之前,由于真空极化和磁化效应,真空非线性已经开始出现[13-14]。由于这种非线性效应反映了真空的一些内在特性,因此引起了广泛的关注[15]。
本文基于QED效应修正的麦克斯韦方程组和流体方程组,得到了超强线极化脉冲激光在e-p等离子体中传播时,脉冲包络所满足的非线性Schrödinger方程,并对其进行数值求解。结果表明,真空极化和磁化效应产生的非线性与群速度色散之间的竞争能导致高斯型脉冲激光的自压缩,对于长脉冲,这种竞争能使脉冲在压缩后又会产生分裂,最终导致类多孤子结构的形成。
1 基本方程
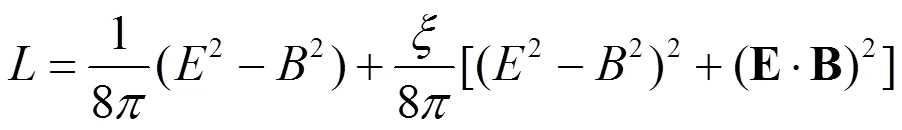

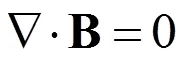


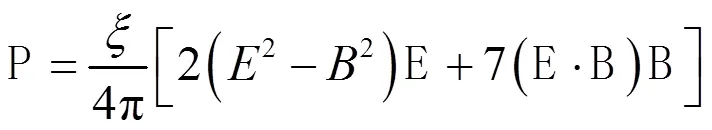
和



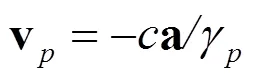

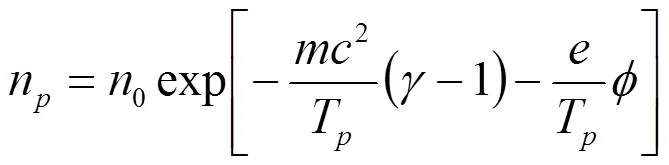



因此,



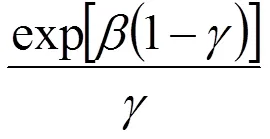

2 结果与讨论
2.1 脉冲自压缩


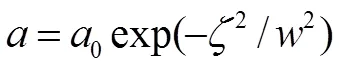


这种自压缩是由于非线性效应和群速度色散的共同作用所导致的[19-21]。由于非线性效应,等离子体的折射指数会随激光强度的变化而变化,从而使脉冲的频率产生啁啾,即自相位调制。这种啁啾过程会引起脉冲频率在不同部位的连续红移或蓝移,在群速度色散作用下,这种啁啾脉冲就可能产生自压缩[19-20]。图1表明,真空极化和磁化效应产生的非线性与群速度色散的共同作用,能使高斯 型入射激光脉冲产生自压缩现象。
2.2 脉冲分裂和类多孤子结构的形成
随着脉冲在e-p等离子体中的传播,分裂后的脉冲最终形成比较稳定的类多孤子结构,如图3所示。
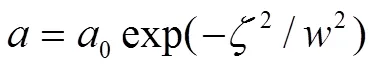
脉冲的分裂以及类多孤子结构的形成,仍然是由于非线性效应和群速度色散共同作用产生的结果。在脉冲传播的初始阶段,自相位调制占主导作用,因此脉冲被压缩,如图2(b)所示。此时,如果非线性效应和群速度色散之间能达到平衡,则可能形成准静态的孤波[10]。对脉宽较大的脉冲,在自压缩过程中,脉冲的变窄效应超过变宽效应,从而导致高阶孤子的形成。当脉冲被压缩到一定的程度,群速度色散将其主导作用,脉冲又将被展宽。脉冲激光传播过程中,在脉冲的中部会产生最强的相位调制效应,使得脉冲频率产生啁啾。这种啁啾能导致脉冲的高阶孤子分裂。随着脉冲的传播,分裂后的脉冲又能重新被压缩[19-20]。更细致的数值结果表明,这种压缩—分裂—压缩的过程将重复几次,最后,脉冲演化成较为稳定的类多孤子结构。
3 结论

[1] Lu Gaimin, Liu Yue, Yu M Y. Exact electrostatic waves in electron-positron plasmas[J]. Phys. Scr.,2010,81: 045503.
[2] Asenjo F A, Muñoz V, Valdivia J A, et al. Circularly polarized wave propagation in magnetofluid dynamics for relativistic electron-positron plasmas[J]. Phys. Plasmas, 2009,16: 122108.
[3] Liang E. Generation and astrophysical applications of relativistic pair plasmas with ultra-intense lasers[J]. AIP Conf. Proc., 2002,611: 369-374.
[4] Liang E P, Wilks S C, Tabak M. Pair Production by Ultraintense Lasers[J]. Phys. Rev. Lett., 1998, 81: 4887-4890.
[5] Marklund M, Shukla P K. Nonlinear collective effects in photon-photon and photon-plasma interactions[J]. Rev. Mod. Phys., 2006,78: 591-640.
[6] Shukla P K, Marklund M, Eliasson B. Nonlinear dynamics of intense laser pulses in a pair plasma[J]. Phys. Letts. A, 2004,324: 193-197.
[7] Bulanov S S, Fedotov A M, Pegoraro F. Damping of electromagnetic waves due to electron-positron pair production[J]. Phys. Rev. E, 2005,71: 016404.
[8] Lontano M, Bulanov S, Koga J. Relativistic electromagnetic solitons in a high temperature plasma[J]. AIP Conf. Proc., 2002,611: 157-163.
[9] Bulanov S V, Esirkepov T Zh, Hayashi Y, et. al. Hayashi Y, et al. Extreme field science[J]. Plasma Phys. Control. Fusion, 2011,53: 124025.
[10] Hu Q L, Xiao G L, Yu X G, et.al. Vacuum polarization and magnetization effects in ultra-intense laser pulse-pair plasmas[J]. Phys. Plasmas, 2012,19: 042306.
[11] Mourou G A. Optics in the relativistic regime[J]. Rev. Mod. Phys., 2006, 78: 309-371.
[12] Bulanov S S, Mur V D, Narozhny N B, et al. Multiple Colliding Electromagnetic Pulses: A Way to Lower the Threshold of e+e- Pair Production from Vacuum[J]. Phys. Rev. Lett., 2010, 104: 220404.
[13] Di Piazza A, Hatsagortsyan K Z, Keitel C H. Nonperturbative Vacuum-Polarization Effects in Proton-Laser Collisions[J]. Phys. Rev. Lett., 2008, 100: 010403.
[14] Di Piazza A, Hatsagortsyan K Z, Keitel C H. Enhancement of vacuum polarization effects in a plasma[J]. Phys. Plasmas, 2007, 14: 032102.
[15] Bulanov S V, Esirkepov T, Tajima T. Light Intensification towards the Schwinger Limit[J]. Phys. Rev. Lett., 2003, 91: 085001.
[16] Ferrando A, Michinel H, Seco M, Tommasini D. Nonlinear Phase Shift from Photon-Photon Scattering in Vacuum[J]. Phys. Rev. Lett., 2007, 99: 150404.
[17] Baifei Shen, Yu M Y, Wang Xiaofang. Photon-photon scattering in a plasma channel[J]. Phys. Plasmas, 2003, 10: 4570-4571.
[18] Lundin J, Brodin G, Marklund M. Short wavelength quantum electrodynamical correction to cold plasma-wave propagation[J]. Phys. Plasmas, 2006, 13: 102102.
[19] 张秋菊, 武慧春, 王兴海, 等. 超短激光脉冲在等离子体中的分裂以及类孤子结构的形成[J].物理学报,2007, 56:7106-7113.
[20] 栾仕霞, 张秋菊, 武慧春, 等. 激光脉冲在等离子体中的压缩分裂[J].物理学报, 2008, 57: 3646-3652.
[21] Shorokhov O, Pukhov A, Kostyukov I. Self-Compression of Laser Pulses in Plasma[J]. Phys. Rev. Lett., 2003, 91: 265002.
Pulse splitting and multi-solitons-like structure formation of ultra-intense laser pulse in electron-positron plasmas
*HU Qiang-lin, YU Xiao-guang
(School of Mathematics and Physics Jinggangshan University, Ji’an, Jiangxi 343009, China)
The propagation characteristic of a linearly polarized ultra-intense laser pulse propagating in electron-positron plasmas are investigated by solving the modified nonlinear Schrödinger equation numerically. The results show that the competition of the vacuum polarization and magnetization nonlinearity and group velocity dispersion can result in the compression of an initially Gaussian laser pulse. For long pulse, the competition can split the pulse, and lead to the formation of a relatively stable multi-solitons-like structure.
vacuum polarization and magnetization; electron-positron plasma; ultra-intense laser pulse
1674-8085(2013)05-0013-06
O539
A
10.3969/j.issn.1674-8085.2013.05.004
2013-05-12;
2013-08-16
国家自然科学基金项目(11064005),江西省自然科学基金项目(2010GQW0030),江西省原子与分子重点学科(2011-2015)项目
*胡强林(1976-),男,江西永新人,副教授,博士,主要从事强场物理研究(E-mail:qlhu@jgsu.edu.cn);
余晓光(1963-),男,江西万安人,教授,硕士,主要从事强场物理研究(E-mail:yxg0796@sino.com) .
