基于Loop细分的自适应细分曲面算法

吴元翠



基于Loop细分的自适应细分曲面算法

吴元翠

(安徽农业大学理学院应用数学研究所，安徽，合肥 230036)

首先研究了传统的Loop细分曲面算法，通过分析发现随着细分次数的增多细分算法中三角形网格片数增长过快。针对这一问题提出一种自适应细分曲面算法。算法根据相邻两个三角形面上的法向量的夹角，判断细分网格中较为光滑和非光滑的区域。实验结果表明，算法提高了数据处理速度，并且模型简单易实现。

细分曲面；Loop细分；自适应细分

0 引言

然而，细分网格在应用中面临的的难题是细化光滑度与数据量成几何级数剧增的矛盾，针对这一问题，一种可行的办法是采用自适应细分曲面算法实现细分。自适应细分曲面算法是根据一定的光滑性和连续性的要求，判断细分网格中较为光滑的区域和非光滑的区域，从而只对非光滑区域进行细分，以达到降低网格数提高效率的目的。由于存在不同的细分曲面算法，故自适应细分算法的适用性较广。国外Ashish Amresh等人对三角网格自适应细分[4]作了探索，Hamid-Reza提出了一种增量自适应细分[5]，该方法可以根据用户的需求只对选定的区域进行细分。另外，近几年来很多三角形网格的自适应细分方法[5-10]已被提出，但这些算法中有些会产生一些退化三角形，使得部分面片处于不同层，破坏了整体细分曲面的连续性，也有些算法原理复杂，难以实现。

本文提出的基于Loop细分中网格边光滑度的自适应细分算法，以相邻两个三角形网格面的法向量夹角为判据，区分细分网格中较为光滑和非光滑的区域，从而达到自适应细分的目的，能够有效的降低细分过程三角网格片数的增加量。

1 Loop细分算法

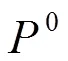
V-顶点的计算规则为:

E-顶点的计算规则为：

其细分模板如图1所示：

图1 Loop细分曲面算法

Fig.1 The Loop subdivision surface algorithm

2 基于边光滑度的自适应细分算法

目前广泛采用的自适应细分的判据是网格顶点与对应的极限位置的距离以及顶点的曲率等。这些算法中有些会产生一些退化三角形，使得部分面片处于不同层，破坏了整体细分曲面的连续性，也有些算法原理复杂，难以实现。本文提出一种基于Loop三角形网格边光滑度的自适应细分算法，以相邻两个三角形面片的外法向量的夹角作为判据确定各边的光滑性，从而达到自适应细分的目的。

2.1 算法原理

图2 自适应细分算法

(4)在下一级细分中，光滑边的中点取为E-点；如果顶点对应的边均为光滑边，则标记该顶点为不动点，在下一级细分中保持其几何位置不变。当一个面片的所有顶点都为不动顶点时，该面片为不动面片，在后面的细分中，不再对该面片细分。

每一次细分前，都按照上述算法对控制网格进行检测，对于非不动顶点和非光滑边，按照Loop细分的几何规则完成本次细分中新的边点和顶点的计算，并按照其拓扑规则产生新的网格。

2.2 裂缝处理

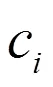
图3 裂缝处理

2.3 实例分析

为了验证本文算法的有效性，利用 C++和OPENGL 图形函数库，在 VC++6.0 环境编程实现了相应算法，对原始面片数为 319的模型两次细分，如图4所示。

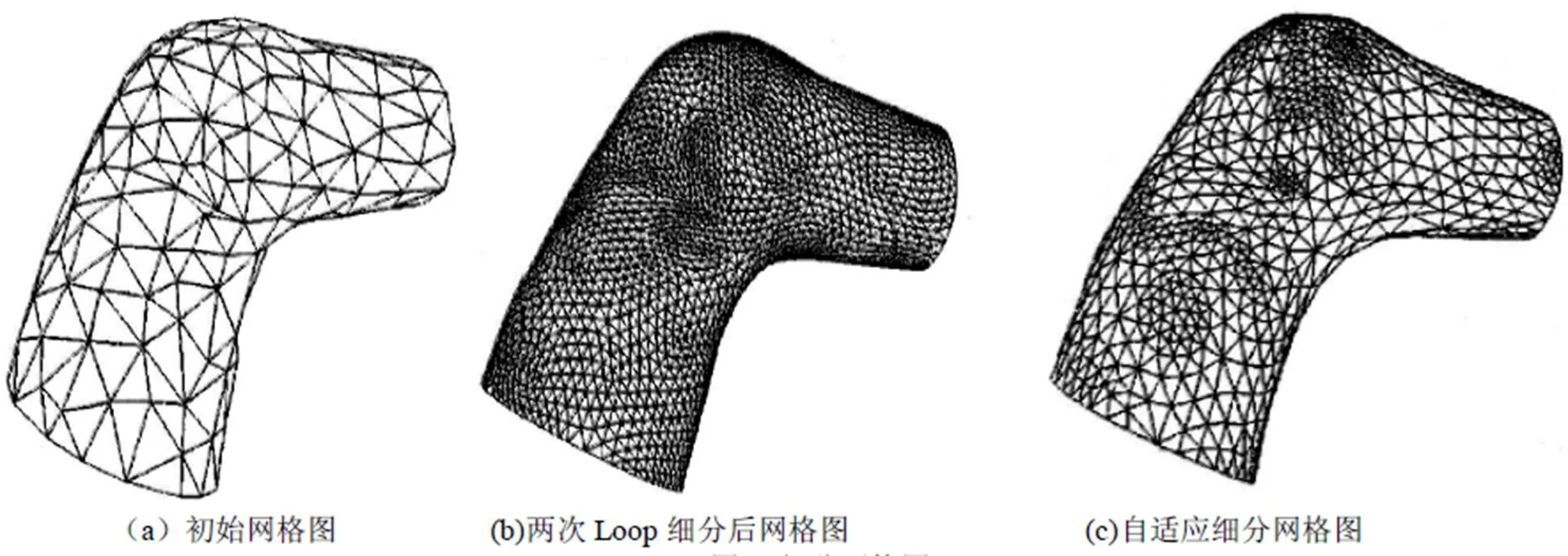
图4 细分网格图

3 结论

综上所述，本文提出的算法在进行自适应细分的时能较好地实现降低模型中的存储量和运算量；能准确的分辨模型的较光滑和较粗糙区域。另外，作者在后续研究工作中，将对算法的规则和设计进行适当修改，使其能更广泛应用于其他细分曲面模式中。

[1] Loop C.Smooth Subdivision Surfaces Based on Triangles [D]. Utah: University of Utah, 1987.

[2] Catmul E, Clark J. Recursively generated B-spline surfaces Oil topological meshes [J].Computer Aided Design, 1978,l0(6):350-355.

[3] Doo D, Sabin M. Behaviour of recursive division surfaces Deal extraordinary points[J].Computer Aided Design, 1978, 10 (6):156-160.

[4] Amresh A, Farin G, Razdan A. Adaptive Subdivision Yw. Hemes for triangle Meshes [M]. Arizona: Arizona State University, 2000.

[5] 钟大平,周来水,周海. 自适应混合细分算法研究 [J]. 机械科学与技术 ,2004,23(9):1090-1092.

[6] 王艳艳,张荣国,王蓉,等. 向量线性相关的三角网格自适应 Loop 细分方法 [J]. 工程图学学报 ,2009,1: 91-96.

[7] 赵宏庆,彭国华,叶正麟,等. 自适应细分方法进行曲面造型 [J]. 计算机应用研究. 2006, 9:72-76.

[8] 李桂清,吴壮志,马维银.自适应细分技术研究进展[J]. 计算机辅助设计与图形学报,2006,18(12): 1789-1799.

[9] 吴剑煌,刘伟军,王天然. 面向三角网格的自适应细分[J]. 计算机工程 , 2006 , 32(12):14-16.

[10] 李李,王亚平.裁剪曲面自适应三角化剖分 [J].计算机应用, 2006, 26 : 2-13.

[11] 孙大松,鞠志涛,孙立镌.约束自适应Loop曲面细分 [J]. 计算机应用研究 ,2012,29(9):3506-3508.

Adaptive subdivision surface algorithm based on the Loop subdivision

WU Yuan-cui

(Institute of Applied Mathematics, Anhui Agricultural University, Hefei, Aihui 230036, China)

Firstly, the traditional Loop subdivision surface algorithm is studied. The analysis show that the increase of the number of triangular mesh is growing too fast in the traditional Loop subdivision algorithm. Secondly, in order to solve this problem, an adaptive subdivision surface algorithm is given. This algorithm bases on the included angle of the two normal vector of the two adjacent triangles to judge the more smooth and nonsmooth area in subdivision grid, than subdivides the nonsmooth area only. Finally, the experimental results show that this algorithm improves the speed of subdivision processing, and the model is easy to implement.

subdivision surface; Loop subdivision algorithm; adaptive subdivision algorithm

1674-8085(2013)05-0041-04

TP391

A

10.3969/j.issn.1674-8085.2013.05.010

2013-03-13；

2013-05-26

吴元翠(1980-)，女，安徽凤阳人，讲师，硕士生，主要从事计算机辅助几何设计、计算机图形学、数值计算等研究( E-mail:wuyuancui@ahau.edu.cn).