范畴L-CTop同构范畴L-FTop

王国朋，孟广武

范畴-CTop同构范畴-FTop

*王国朋，孟广武

（聊城大学数学科学学院，山东，聊城 252059）

对任意完备的Heyting 代数，引入了-拓扑的塔的概念，并证明了其构成的范畴与-模糊拓扑范畴是同构的。

-拓扑；-模糊拓扑；范畴

0 引言

自从Chang把模糊集理论引入拓扑以来，很多学者从不同的角度出发讨论了各种各样的模糊拓扑理论以及它们之间的关系[1-6]。对任意完全分配格，文献[3-6]以不同的方式证明了每一个-模糊拓扑都对应于一族满足某些条件的-拓扑。本文将继续研究-模糊拓扑和-拓扑的关系。如未加说明本文中的总代表任意的完备的Heyting代数（满足第一无限分配律的完备格）。我们的目的是引入-拓扑的塔的概念，并证明其构成的范畴与-模糊拓扑范畴是同构的。值得注意的是，本文中的塔与文[5]中的塔是不同的概念。另外，有关范畴的概念和符号请参考文献[7]。

1 主要结果

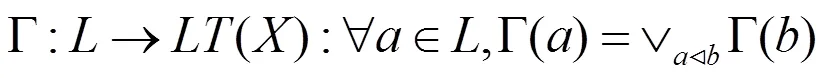
由命题1.1-1.5可以得到定理1.1。

定理1.1 范畴-CTop和范畴-FTop之间存在一个同构：

到此不难看出，集合上的每一个-模糊拓扑都是由一族以为指标集的-拓扑按照从大到小的顺序粘接起来得到的，其形状恰似一塔。

[1] Houhle U, Sostak A. Mathematics of Fuzzy Sets , Logic ,Topology and Measure Theory [M].Boston : Kluwer Academic Publishers , 1999.

[2] 王国俊. L-fuzzy 拓扑空间论[M].西安：陕西师范大学出版社,1988.

[3] 金秋,李令强,孙守斌.L-模糊拓扑空间的新表示定理[J].西南师范大学学报,2011,36(5):56-58.

[4] Fang Jinming. Categories isomorphic to L-FTOP[J]. Fuzzy Set And Systems,2006(157):820-831.

[5] Zhang Dexue. On the relationship between several basil category in fuzzy topology [J]. Questions Mathematicae,2002(25):289-301.

[6] Zhang Jie, Shi Fugui, Zheng Chongyou. On-fuzzy topological spaces[J].Fuzzy Set and Systems,2005(149): 473-484.

[7] Adamek J, Herrlich H, Strecker G E. Abstract and Concrete Categories [M]. New York: Wiley, 1990.

Categories-CTop isomorphic to-FTop

*WANG Guo-peng，MENG Guang-wu

(School of Mathematics Science, Liaocheng University, Liaocheng, Shandong 252059, China)

The notion of tower for- topologies is introduced for arbitrary complete Heyting algebra. It is proved that the category of towers of-topological spaces is isomorphic to the category of-fuzzy topological spaces.

- topology;-fuzzy topology; category

1674-8085(2013)05-0001-03

O159.1

A

10.3969/j.issn.1674-8085.2013.05.001

2012-12-27；

2013-05-26

山东省中青年科学家科研奖励基金项目（BS2010SF004）

*王国朋(1985-)，男，河南安阳人，硕士生，主要从事不确定信息处理研究( E-mail:happywgp2008@163.com);

孟广武(1958-)，男，山东莱芜人，教授，主要从事模糊系统理论研究( E-mail:menggw@lcu.edu.cn).