空气阻力与球体运动速度的函数关系

代超超 杨 凯 龙姝明

（陕西理工学院物理系，陕西 汉中 723005）

运动物体所受空气阻力的大小与物体的形状、几何大小、运动速度、密度、表面光洁度等因素有关，文献［1］认为当物体高速运动时空气阻力f正比于速度的平方v2；低速运动时阻力f 正比于速度v，但是这些研究结果都是特定情况下的结论.本文通过对乒乓球在空气阻力和重力作用下的落体及其多次反弹运动的研究，给出了轻质球体所受空气阻力与速度的函数关系，并提出了这类问题的科学有效的研究方法.

1 考虑空气阻力的乒乓球落体及其反弹运动的动力学方程

假定α≥1，合并式（1）和（2）为

其中，“｜｜”表示取绝对值运算.初始位移记为x0，初始速度记为v0.很明显，式（3）是二阶非线性非齐次常微分方程，α＝1和α＝2的解析解为

一般情况下，α取非整数值，方程式（3）的解析解不存在，只能用数值方法解方程.用数值方法解式（3）时，一要给定方程中所有参数（m，g，k，α）的具体数值，二要给定初始位移x0和初始速度v0，三要选定解方程的时区时间起止点.

由于乒乓球下落及其反弹运动受空气阻力作用，各时段的起止时间未知，各时段开始时刻的速度v0和位移x0各不相同而且未知，这给数值求解带来困难.要通过编程，分时段求解落体运动微分方程，最后叠加得到方程在整个时间段的解，这一过程就只能一步步来，即选定方程中各参数一组数值，从头开始，逐段求解，每当解得当前时段的运动，就可能给出下一时段的“初始”条件及开始时刻，为下一段数值方法求解准备好条件.

2 乒乓球落体运动的动力学方程求解思路

假设与地面的碰撞是弹性碰撞，要研究乒乓球下落后多次与地面碰撞的反弹运动特征，只能采用数值方法求解式（3）.由于每次反弹运动的初始条件都不一样，且必须在求解了前面各次反弹运动时段起止点及前一次反弹落地的末速度之后，才能知道这次反弹的开始时间和开始速度，所以必须采取分时段，依次求解每次反弹运动方程的方法.

记乒乓球首次下落的起始时间为t0＝0，初速度v0＝0，初始位移x0＝h0，各次反弹过程的初始位移均为零.求式（3）的数值解，得到第一次球与地面碰撞的时点t1和碰撞时刻前的速度v1－，以t1作为第一次反弹运动的起始时间，碰撞时刻后反弹的开始速度v1＋＝－v1－，再次求解式（3），可得到第一次反弹过程的落地时点t2和落地末速度v2－，从而得到第二次反弹运动的开始时点t2和初始初速度v2＋＝－v2－.以此类推，便可以求得各次反弹运动的开始时点及初始速度，进而求得乒乓球各次反弹运动随时间演化的规律.下面给出采用Mathematica软件编程［2］求解落体反弹运动规律的主要思路.

设乒乓球质量m＝0.0027kg，重力加速度g＝9.8m/s2，选择初始高度为h0＝2m .取空气阻尼系数k＝0.001，速度幂次α＝1.1，求解时间段为（0，tf），tf为首次下落过程的预估时间，tf大于等于首次真实落地时间点t1，v为乒乓球接触地面时点之前的末速度，分别将各段运动中的末速度v，末时刻tn，最大上升高度h 记录在数表vt，tt，H中.利用Mathematica 8.0内部函数NDSolve［］解微分方程（3），得到首次下落过程数值解所需程序段为

为求解乒乓球各次反弹运动特征，设th为乒乓球每次反弹上升最大高度的时点，h为时点th对应的最大上升高度，t1是落地时点，调用Mathematica8.0的While［］函数编写循环程序

下面分别给出两组不同（k，α）值的理论计算数据，n表示乒乓球运动下落反弹次数编号，取前9次的计算数据列于表1中.

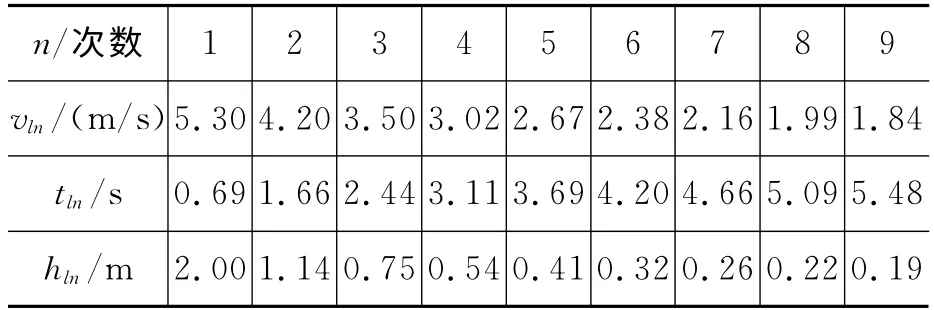
表1 （k＝0.001 53，α＝1.2）

表2 （k＝0.000 62，α＝2.0）

由表1和表2可以看出，对于给定的每组（k，α）值，随着乒乓球碰撞次数的增加，每次反弹上升最大高度、触地前的速度、落地时间都逐渐减小，限于篇幅，这里不画乒乓球位移随时间演化的曲线.

3 实验数据与理论计算的比较

乒乓球落体反弹运动试验记录了每次乒乓球落地时间t/s和弹起的最大高度（h/m）（见表3）与乒乓球运动下落次数n的关系（见图1～图6）.为了检验理论计算数据与实验数据的吻合程度，在程序中多次改变速度幂次α，对于每个α值又调整k值大小，比较乒乓球每次反弹高度、落地时间理论值与实验值，借助关系图1～图6和相应理论分析，最终找到理论与实验符合较好的α值与k 值.

表3 乒乓球下落反弹过程中各次落地时间及反弹最大高度实验数据

表4给出不同（k，α）值的理论数据与实验数据的 吻 合 程 度，ge、be、fin 分 别 表 示 一 般、较好、好.

表4 不同α与k 值时理论与实验吻合程度

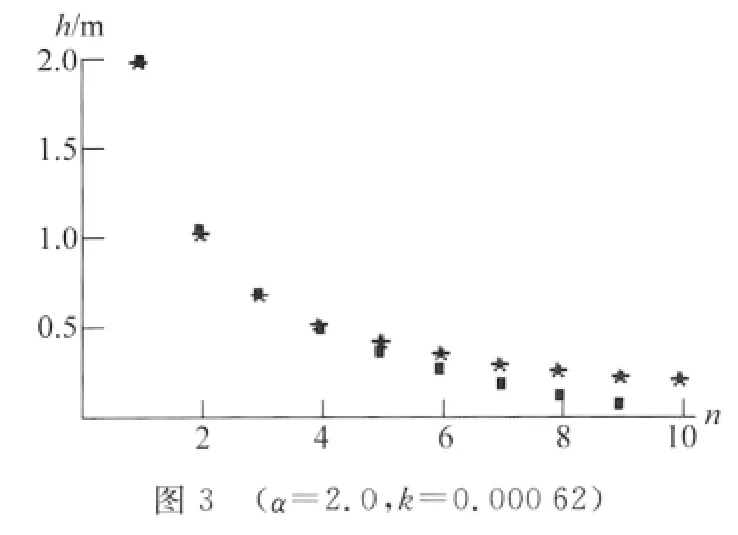
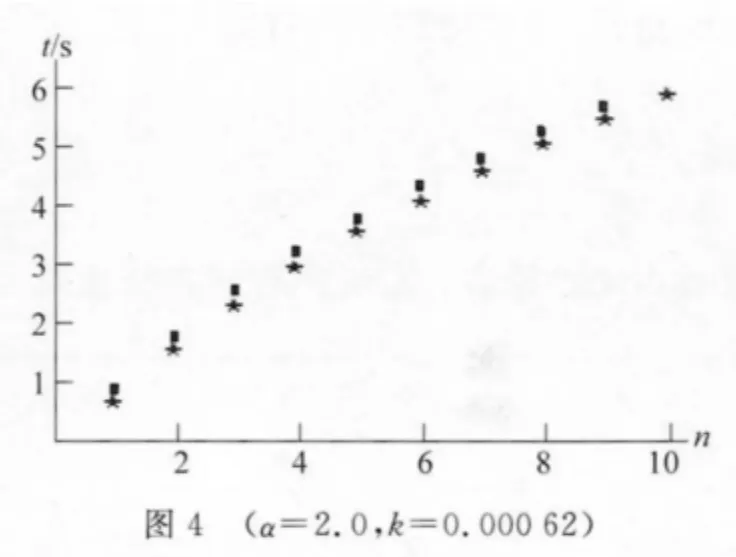
分别以每次着地时间t/s、反弹最大高度h/m为横坐标，以乒乓球运动下落次数n 为纵坐标画图，正方形点代表试验数据，五角星代表不同组（k，α）值下理论数据，给出α＝2.5，k＝0.000 32；α＝2.0，k＝0.000 62；α＝1.2，k＝0.001 53三组不同实验数据的对比图.

对比图1～图6，我们可以清楚地看出当α＝1.2，k＝0.001 53时，对应理论计算数据与实验数据吻合最好.如表3所示，当α 值在1.4～1.0之间时，理论数据与实验数据都有比较好的吻合度.

由于乒乓球大小固定、质地均匀、表面光洁、随机性弱，运动时所受空气阻力规律相对固定.实际上，乒乓球在着地时，与地面发生的碰撞不是完全弹性碰撞，碰撞过程有能量损失，上面各图中实验测量反弹高度总是低于理论计算值，这就说明碰撞过程确实有能量损失.

如果研究球体密度变大，或者几何形状对称性降低，表面粗糙，运动时所受空气阻尼系数k 和依赖于速度的幂次α 一定不同于乒乓球的情况，而且有随机性，这有待进一步研究.

4 结语

通过本文的研究，发现乒乓球在空气阻力和重力作用下的落体运动过程中，所受空气阻力规律f＝kvα中α 取值范围为1.4到1.0.这一研究结果是对文献［3］给出的“低速物体所受空气阻力与速度一次方成正比”结论的进一步修正和完善.本文所采用的分时段数值方法求解非线性物理系统演化规律的思想，对于处理同类问题，有方法论的启示.

［1］蔡志东，陆建隆.考虑空气阻力时铅球最佳投射角的参数方程和实用方程［J］.大学物理，2006，25（10）：16－22.

［2］龙姝明，朱杰武，孙彦清，等.数学物理方法＆ Mathematica［M］.西安：陕西人民出版社，2002.343－441.

［3］梁兵，甘皓元.在实验室中利用自由落体测定空气阻力系数［J］.百色物理学报，2009，22（6）：58－60.